L'étude de la position relative de droites et de plans dans l'espace se poursuit, et on étend le produit scalaire à l'espace en conservant les propriétés du produit scalaire dans le plan.
Dans tout le chapitre, on munit l'espace du repère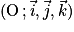 .
.
Dans tout le chapitre, on munit l'espace du repère
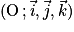 .
.I. Quelles sont les propriétés des coordonnées d'un vecteur dans l'espace ?
Pour tout point M de l'espace, il existe un unique triplet de réels (x, y, z) tels que 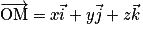 .
.
Pour tout vecteur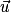 de l'espace, il existe un unique triplet de réels (x, y, z) tels que
de l'espace, il existe un unique triplet de réels (x, y, z) tels que 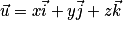 .
.
Propriétés :
Soient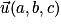 ,
, 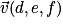 deux vecteurs de l'espace, et k un réel.
deux vecteurs de l'espace, et k un réel.
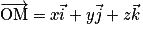 .
.Pour tout vecteur
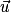 de l'espace, il existe un unique triplet de réels (x, y, z) tels que
de l'espace, il existe un unique triplet de réels (x, y, z) tels que 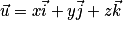 .
.Propriétés :
Soient
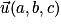 ,
, 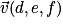 deux vecteurs de l'espace, et k un réel.
deux vecteurs de l'espace, et k un réel.• La somme des deux vecteurs 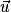 et
et 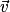 se note :
se note : 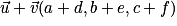 .
.
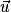 et
et 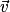 se note :
se note : 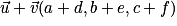 .
.• Le produit du vecteur 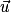 par le scalaire k se note :
par le scalaire k se note : 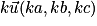 .
.
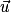 par le scalaire k se note :
par le scalaire k se note : 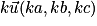 .
.Soient 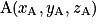 et
et 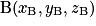 deux points de l'espace.
deux points de l'espace.
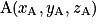 et
et 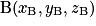 deux points de l'espace.
deux points de l'espace.• Le vecteur 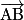 a pour coordonnées
a pour coordonnées 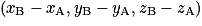 .
.
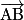 a pour coordonnées
a pour coordonnées 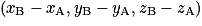 .
.• Le milieu du segment [AB] a pour coordonnées 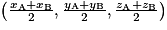 .
.
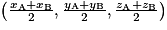 .
.Exemple : Soit le pavé droit ABCDEFGH. 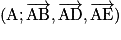 est un repère de l'espace. On a, par exemple, A (0, 0, 0) ; C (1, 1, 0) ; G (1, 1, 1). Le vecteur
est un repère de l'espace. On a, par exemple, A (0, 0, 0) ; C (1, 1, 0) ; G (1, 1, 1). Le vecteur 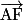 a pour coordonnées (1, 0, 1). Le milieu de [FG] a pour coordonnées (1 ; 0,5 ;1).
a pour coordonnées (1, 0, 1). Le milieu de [FG] a pour coordonnées (1 ; 0,5 ;1).
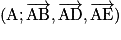 est un repère de l'espace. On a, par exemple, A (0, 0, 0) ; C (1, 1, 0) ; G (1, 1, 1). Le vecteur
est un repère de l'espace. On a, par exemple, A (0, 0, 0) ; C (1, 1, 0) ; G (1, 1, 1). Le vecteur 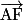 a pour coordonnées (1, 0, 1). Le milieu de [FG] a pour coordonnées (1 ; 0,5 ;1).
a pour coordonnées (1, 0, 1). Le milieu de [FG] a pour coordonnées (1 ; 0,5 ;1).II. Quelles sont les propriétés du produit scalaire ?
Soient 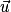 et
et 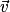 deux vecteurs de l'espace, et les points A, B et C tels que
deux vecteurs de l'espace, et les points A, B et C tels que 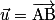 et
et 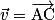 , avec les points A, B et C coplanaires. Le produit scalaire de
, avec les points A, B et C coplanaires. Le produit scalaire de 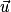 et
et 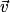 (noté
(noté 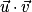 ) est le réel
) est le réel 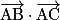 .
.
Propriétés : On munit l'espace d'un repère orthonormé.
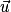 et
et 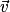 deux vecteurs de l'espace, et les points A, B et C tels que
deux vecteurs de l'espace, et les points A, B et C tels que 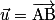 et
et 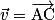 , avec les points A, B et C coplanaires. Le produit scalaire de
, avec les points A, B et C coplanaires. Le produit scalaire de 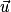 et
et 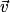 (noté
(noté 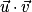 ) est le réel
) est le réel 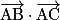 .
.Propriétés : On munit l'espace d'un repère orthonormé.
• Soient 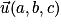 et
et 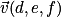 deux vecteurs de l'espace, alors :
deux vecteurs de l'espace, alors : 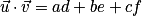 .
.
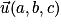 et
et 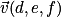 deux vecteurs de l'espace, alors :
deux vecteurs de l'espace, alors : 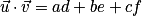 .
.• Soient deux vecteurs 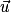 et
et 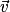 . On a :
. On a : 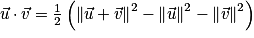 .
.
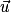 et
et 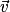 . On a :
. On a : 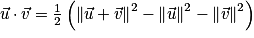 .
.• On obtient alors également : 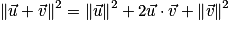 .
.
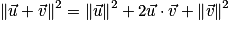 .
.Exemples : Soit un cube ABCDEFGH et I le milieu de [EF]. 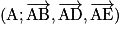 est un repère orthonormé de l'espace.
est un repère orthonormé de l'espace.
On a, par exemple, I (0,5 ; 0 ; 1), A (0, 0, 0), B (1, 0, 0) et H (0, 1, 1).
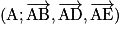 est un repère orthonormé de l'espace.
est un repère orthonormé de l'espace.On a, par exemple, I (0,5 ; 0 ; 1), A (0, 0, 0), B (1, 0, 0) et H (0, 1, 1).
• On a alors : 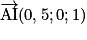 et
et 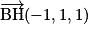 .
.
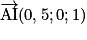 et
et 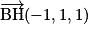 .
.• On peut calculer 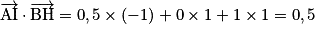 .
.
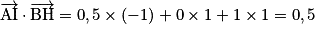 .
.On a : 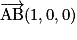 et
et 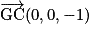 . Alors
. Alors 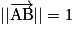 et
et 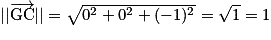 .
.
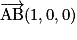 et
et 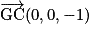 . Alors
. Alors 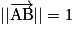 et
et 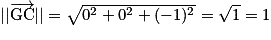 .
.• On a alors 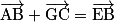 et
et 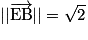 .
.
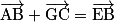 et
et 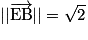 .
.• On peut donc calculer 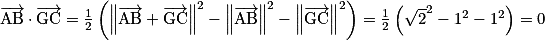 .
.
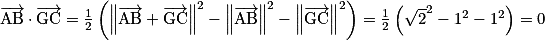 .
.III. Comment caractériser l'orthogonalité entre deux vecteurs ?
Propriétés : On munit l'espace d'un repère orthonormé.
Soient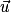 et
et 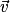 deux vecteurs de l'espace, et trois points A, B et C tels que
deux vecteurs de l'espace, et trois points A, B et C tels que 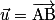 et
et 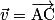 .
.
On dit que les vecteurs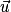 et
et 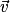 sont orthogonaux si et seulement si :
sont orthogonaux si et seulement si :
Soient
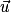 et
et 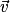 deux vecteurs de l'espace, et trois points A, B et C tels que
deux vecteurs de l'espace, et trois points A, B et C tels que 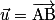 et
et 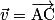 .
.On dit que les vecteurs
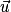 et
et 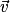 sont orthogonaux si et seulement si :
sont orthogonaux si et seulement si :• les droites (AB) et (AC) sont perpendiculaires lorsque les points A, B et C sont dans le même plan ;
• le produit scalaire entre les vecteurs 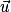 et
et 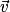 est nul :
est nul : 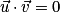 .
.
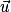 et
et 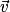 est nul :
est nul : 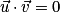 .
.Exemple : Soit un cube ABCDEFGH.
• Les vecteurs 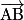 et
et 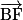 sont orthogonaux, car les droites (AB) et (BF) sont perpendiculaires et dans le même plan (ABF).
sont orthogonaux, car les droites (AB) et (BF) sont perpendiculaires et dans le même plan (ABF).
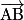 et
et 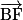 sont orthogonaux, car les droites (AB) et (BF) sont perpendiculaires et dans le même plan (ABF).
sont orthogonaux, car les droites (AB) et (BF) sont perpendiculaires et dans le même plan (ABF).• Les vecteurs 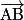 et
et 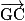 sont également orthogonaux, car
sont également orthogonaux, car 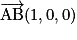 et
et 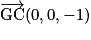 . Donc
. Donc 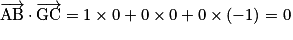 .
.
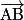 et
et 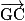 sont également orthogonaux, car
sont également orthogonaux, car 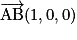 et
et 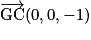 . Donc
. Donc 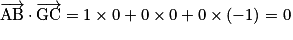 .
.IV. Comment caractériser la distance entre deux points dans l'espace ?
Propriété : La distance AB entre les deux points A à B est égale à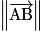 .
.Exemple : Soit ABCD un tétraèdre et I milieu de [BC]. Soit
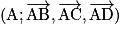 un repère orthonormé de l'espace.
un repère orthonormé de l'espace.On a D (0, 0, 1) et I (0,5 ; 0,5 ; 0). Ainsi
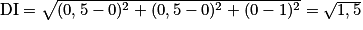 .
.V. Que faut-il retenir sur les mesures d'angle ?
Propriété : Soient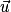 et
et 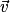 deux vecteurs de l'espace, et les points A, B et C tels que
deux vecteurs de l'espace, et les points A, B et C tels que 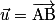 et
et 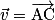 .
.Le produit scalaire des deux vecteurs
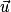 et
et 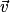 est aussi donné par la formule :
est aussi donné par la formule : 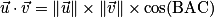 .
.Exemple : Soit un cube ABCDEFGH et I milieu de [BF].
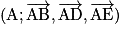 est un repère orthonormé de l'espace.
est un repère orthonormé de l'espace.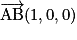 et
et 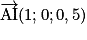 . Alors et
. Alors et 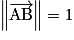 et
et 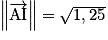 .
.D'une part,
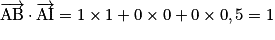 .
.D'autre part,
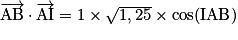 .
.Alors
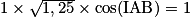 , d'où
, d'où 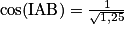 et
et 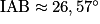 .
.VI. Que faut-il retenir sur la notion de vecteur normal ?
Propriété : Un vecteur normal à un plan est un vecteur non nul. Un vecteur non nul est un vecteur normal d'un plan P de vecteurs directeurs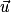 et
et 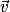 si et seulement s'il est orthogonal aux vecteurs
si et seulement s'il est orthogonal aux vecteurs 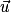 et
et 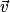 .
.Exemple : La notion de vecteur normal permet d'interpréter vectoriellement l'orthogonalité de droites et de plans. Elle permet aussi de déterminer une équation cartésienne d'un plan dans un repère orthonormal de l'espace, en s'appuyant sur la propriété suivante : le plan passant par A et de vecteur normal
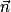 est l'ensemble des points M de l'espace tels que
est l'ensemble des points M de l'espace tels que 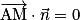 .
.VII. Comment caractériser l'intersection entre une droite et un plan ?
Propriété : On étudie la position relative d'une droite D passant par le point A, de vecteur directeur 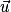 et d'un plan P de vecteur normal
et d'un plan P de vecteur normal 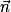 .
.
Si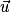 et
et 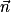 sont orthogonaux, alors la droite D est parallèle au plan P.
sont orthogonaux, alors la droite D est parallèle au plan P.
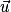 et d'un plan P de vecteur normal
et d'un plan P de vecteur normal 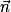 .
.Si
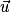 et
et 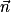 sont orthogonaux, alors la droite D est parallèle au plan P.
sont orthogonaux, alors la droite D est parallèle au plan P.• Si, en outre, le point A appartient au plan P, alors la droite D est incluse dans le plan P.
• Sinon, la droite D est strictement parallèle au plan P, et leur intersection est vide.
Si 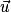 et
et 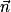 ne sont pas orthogonaux, alors la droite D et le plan P sont sécants, et leur intersection est un point.
ne sont pas orthogonaux, alors la droite D et le plan P sont sécants, et leur intersection est un point.
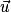 et
et 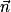 ne sont pas orthogonaux, alors la droite D et le plan P sont sécants, et leur intersection est un point.
ne sont pas orthogonaux, alors la droite D et le plan P sont sécants, et leur intersection est un point.• Si, par ailleurs, 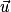 et
et 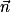 sont colinéaires, alors la droite D est orthogonale au plan P.
sont colinéaires, alors la droite D est orthogonale au plan P.
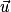 et
et 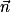 sont colinéaires, alors la droite D est orthogonale au plan P.
sont colinéaires, alors la droite D est orthogonale au plan P.VIII. Comment caractériser l'intersection de deux plans ?
Propriété : On considère deux plans P et P' de vecteurs normaux respectifs 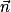 et
et 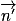 .
.
P et P' sont parallèles si et seulement si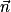 et
et 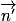 sont colinéaires.
sont colinéaires.
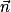 et
et 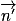 .
.P et P' sont parallèles si et seulement si
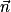 et
et 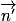 sont colinéaires.
sont colinéaires.• Soit P et P' sont confondus, et leur intersection est un plan.
• Soit P et P' sont strictement parallèles, et leur intersection est vide.
Sinon P et P' sont sécants et leur intersection est une droite.
IX. Comment caractériser la projection orthogonale dans l'espace ?
Propriété : On munit l'espace d'un repère orthonormé. Soient A, B et C trois points de l'espace et H le projeté orthogonal du point B sur la droite (AC).
• 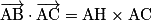 si les vecteurs
si les vecteurs 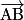 et
et 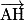 ont le même sens.
ont le même sens.
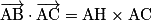 si les vecteurs
si les vecteurs 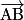 et
et 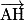 ont le même sens.
ont le même sens.• 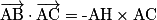 si les vecteurs
si les vecteurs 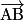 et
et 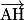 sont de sens contraires.
sont de sens contraires.
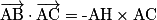 si les vecteurs
si les vecteurs 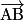 et
et 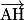 sont de sens contraires.
sont de sens contraires.Exemple : Soit un cube ABCDEFGH et I milieu de [BF]. 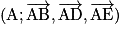 est un repère orthonormé de l'espace.
est un repère orthonormé de l'espace.
On a I (1 ; 0 ; 0,5), A (0, 0, 0) et B (1, 0, 0). De plus, on a : AB = 1 et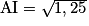 .
.
Le projeté orthogonal de I sur la droite (AB) est le point B.
Donc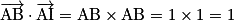 .
.
Conséquence : Soit A un point de l'espace et H le projeté orthogonal du point A sur le plan P de vecteur directeur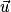 . Alors
. Alors 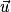 et
et 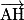 sont orthogonaux, et donc
sont orthogonaux, et donc 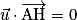 .
.
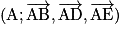 est un repère orthonormé de l'espace.
est un repère orthonormé de l'espace.On a I (1 ; 0 ; 0,5), A (0, 0, 0) et B (1, 0, 0). De plus, on a : AB = 1 et
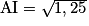 .
.Le projeté orthogonal de I sur la droite (AB) est le point B.
Donc
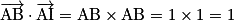 .
.Conséquence : Soit A un point de l'espace et H le projeté orthogonal du point A sur le plan P de vecteur directeur
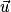 . Alors
. Alors 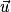 et
et 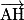 sont orthogonaux, et donc
sont orthogonaux, et donc 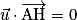 .
.Zoom sur… les propriétés du produit scalaire
Propriété : Formule principale (formule la plus utilisée géométriquement)
Soient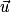 et
et 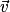 deux vecteurs de l'espace, et les points A, B et C tels que
deux vecteurs de l'espace, et les points A, B et C tels que 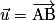 et
et 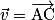 .
.
Le produit scalaire des deux vecteurs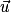 et
et 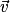 est aussi donné par la formule :
est aussi donné par la formule : 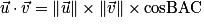 .
.
Propriétés : Soient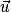 ,
, 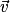 et
et 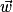 trois vecteurs de l'espace, et k un réel.
trois vecteurs de l'espace, et k un réel.
Soient
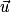 et
et 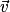 deux vecteurs de l'espace, et les points A, B et C tels que
deux vecteurs de l'espace, et les points A, B et C tels que 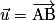 et
et 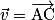 .
.Le produit scalaire des deux vecteurs
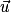 et
et 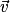 est aussi donné par la formule :
est aussi donné par la formule : 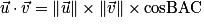 .
.Propriétés : Soient
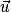 ,
, 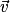 et
et 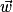 trois vecteurs de l'espace, et k un réel.
trois vecteurs de l'espace, et k un réel.• Symétrie du produit scalaire : 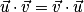 .
.
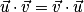 .
.• Bilinéarité du produit scalaire : 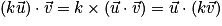 .
.
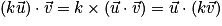 .
.• Distributivité du produit scalaire : 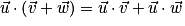 .
.
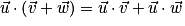 .
.• Le carré scalaire du vecteur 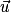 est :
est : 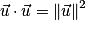 .
.
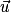 est :
est : 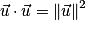 .
.Propriétés : Formules de polarisation
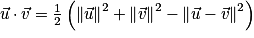
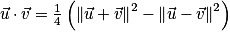
Propriétés : Soient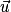 et
et 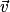 deux vecteurs de l'espace.
deux vecteurs de l'espace.
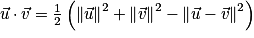
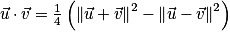
Propriétés : Soient
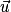 et
et 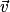 deux vecteurs de l'espace.
deux vecteurs de l'espace.• Si l'un des deux vecteurs est nul, alors leur produit scalaire 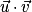 est égal à 0.
est égal à 0.
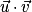 est égal à 0.
est égal à 0.• 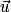 et
et 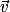 sont orthogonaux si et seulement si leur produit scalaire
sont orthogonaux si et seulement si leur produit scalaire 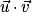 est égal à 0.
est égal à 0.
 et
et 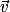 sont orthogonaux si et seulement si leur produit scalaire
sont orthogonaux si et seulement si leur produit scalaire 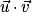 est égal à 0.
est égal à 0.• S'ils sont non nuls et colinéaires, alors : 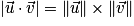 .
.
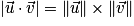 .
.Propriétés géométriques : Soient 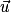 et
et 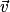 deux vecteurs de l'espace.
deux vecteurs de l'espace.
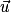 et
et 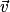 deux vecteurs de l'espace.
deux vecteurs de l'espace.• La droite D de vecteur directeur 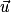 et la droite D' de vecteur directeur
et la droite D' de vecteur directeur 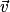 sont orthogonales si
sont orthogonales si 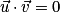 .
.
 et la droite D' de vecteur directeur
et la droite D' de vecteur directeur 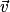 sont orthogonales si
sont orthogonales si 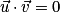 .
.• La sphère de diamètre [AB] est l'ensemble des points M de l'espace tels que : 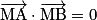 .
.
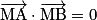 .
.
