L'étude des objets dans l'espace déjà abordée dans les classes antérieures se poursuit avec la caractérisation de droites et de plans par des relations vectorielles.
I. Que faut-il savoir sur les vecteurs dans l'espace ?
Toutes les opérations sur les vecteurs dans un plan se prolongent aux vecteurs dans l'espace.
Propriétés :
Propriétés :
• Les vecteurs 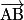 et
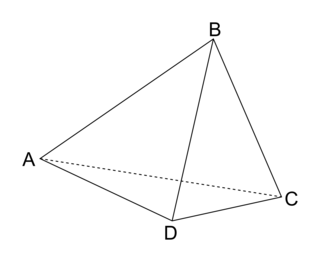
et 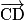 sont égaux si et seulement si ABDC est un parallélogramme. On note alors
sont égaux si et seulement si ABDC est un parallélogramme. On note alors 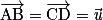 . On dit alors que
. On dit alors que 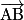 et
et 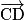 sont des représentants du vecteur
sont des représentants du vecteur 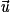 .
.
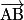 et
et 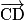 sont égaux si et seulement si ABDC est un parallélogramme. On note alors
sont égaux si et seulement si ABDC est un parallélogramme. On note alors 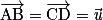 . On dit alors que
. On dit alors que 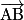 et
et 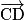 sont des représentants du vecteur
sont des représentants du vecteur 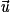 .
.• Soient A un point et 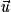 un vecteur. Il existe un unique point M de l'espace tel que
un vecteur. Il existe un unique point M de l'espace tel que 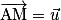 .
.
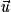 un vecteur. Il existe un unique point M de l'espace tel que
un vecteur. Il existe un unique point M de l'espace tel que 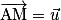 .
.Exemple : Soit un pavé droit ABCDEFGH.
• Le seul point M de l'espace vérifiant 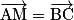 est le point D.
est le point D.
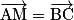 est le point D.
est le point D.• ABCD est un parallélogramme, car 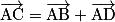 .
.
Exemple : Soit un tétraèdre ABCD. Avec la relation de Chasles, on a :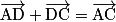 .
.
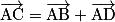 .
.Exemple : Soit un tétraèdre ABCD. Avec la relation de Chasles, on a :
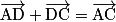 .
.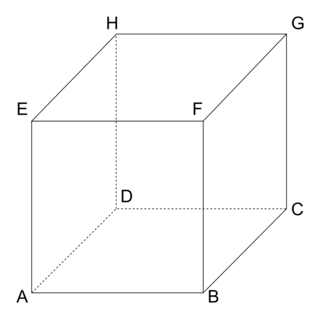 |
On dit qu'un vecteur 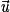 peut être exprimé comme combinaison linéaire des vecteurs
peut être exprimé comme combinaison linéaire des vecteurs 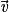 et
et 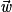 si et seulement s'il existe deux réels a et b tels que
si et seulement s'il existe deux réels a et b tels que 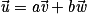 .
.
Exemple : Soit un pavé droit ABCDEFGH. Exprimons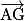 comme combinaison linéaire des vecteurs
comme combinaison linéaire des vecteurs 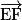 ,
, 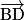 et
et 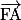 .
.
Avec la relation de Chasles, on peut écrire :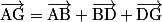 . Comme certains vecteurs du pavé droits sont égaux d'après la propriété du parallélogramme, on obtient :
. Comme certains vecteurs du pavé droits sont égaux d'après la propriété du parallélogramme, on obtient : 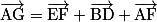 .
.
Finalement, on obtient :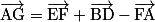 .
.
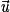 peut être exprimé comme combinaison linéaire des vecteurs
peut être exprimé comme combinaison linéaire des vecteurs 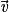 et
et 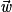 si et seulement s'il existe deux réels a et b tels que
si et seulement s'il existe deux réels a et b tels que 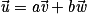 .
.Exemple : Soit un pavé droit ABCDEFGH. Exprimons
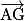 comme combinaison linéaire des vecteurs
comme combinaison linéaire des vecteurs 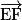 ,
, 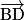 et
et 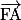 .
.Avec la relation de Chasles, on peut écrire :
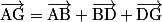 . Comme certains vecteurs du pavé droits sont égaux d'après la propriété du parallélogramme, on obtient :
. Comme certains vecteurs du pavé droits sont égaux d'après la propriété du parallélogramme, on obtient : 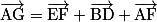 .
.Finalement, on obtient :
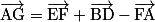 .
.II. Quelle est la caractérisation vectorielle des droites de l'espace ?
Propriétés : Soient A et B deux points distincts de l'espace.
• La droite (AB) est l'ensemble des points M de l'espace tels que 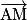 et
et 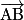 soient colinéaires.
soient colinéaires.
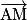 et
et 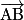 soient colinéaires.
soient colinéaires.• Tout vecteur (non nul) colinéaire à 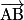 est également un vecteur directeur de (AB).
est également un vecteur directeur de (AB).
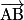 est également un vecteur directeur de (AB).
est également un vecteur directeur de (AB).On dit que 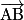 est un vecteur directeur de la droite (AB). On dit aussi que
est un vecteur directeur de la droite (AB). On dit aussi que 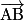 dirige la droite (AB).
dirige la droite (AB).
Exemple : Soient ABCD un tétraèdre et J le milieu de [BC]. Alors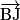 est un vecteur directeur de la droite (BC).
est un vecteur directeur de la droite (BC).
Caractérisation vectorielle d'une droite : Soient A et B deux points distincts de l'espace. M appartient à (AB) si et seulement s'il existe un réel k tel que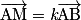 .
.
Remarque : La donnée d'un point et d'un vecteur directeur suffit à caractériser une droite.
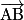 est un vecteur directeur de la droite (AB). On dit aussi que
est un vecteur directeur de la droite (AB). On dit aussi que 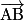 dirige la droite (AB).
dirige la droite (AB).Exemple : Soient ABCD un tétraèdre et J le milieu de [BC]. Alors
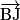 est un vecteur directeur de la droite (BC).
est un vecteur directeur de la droite (BC).Caractérisation vectorielle d'une droite : Soient A et B deux points distincts de l'espace. M appartient à (AB) si et seulement s'il existe un réel k tel que
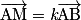 .
.Remarque : La donnée d'un point et d'un vecteur directeur suffit à caractériser une droite.
III. Quelle est la caractérisation vectorielle des plans dans l'espace ?
Caractérisation vectorielle d'un plan : Soient A, B et C trois points non alignés de l'espace. Un point M appartient au plan (ABC) si et seulement si le vecteur 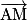 est égal à une combinaison linéaire des vecteurs
est égal à une combinaison linéaire des vecteurs 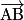 et
et 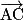 .
.
On dit alors que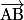 et
et 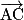 sont des vecteurs directeurs du plan (ABC).
sont des vecteurs directeurs du plan (ABC).
Exemples :
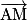 est égal à une combinaison linéaire des vecteurs
est égal à une combinaison linéaire des vecteurs 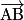 et
et 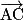 .
.On dit alors que
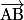 et
et 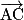 sont des vecteurs directeurs du plan (ABC).
sont des vecteurs directeurs du plan (ABC).Exemples :
• Soit ABCDEFGH un cube de centre O. Le point O appartient au plan (AFG). En effet, on a 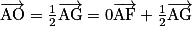 .
.
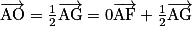 .
.• Soit ABCD un tétraèdre. Soit E le point de l'espace qui vérifie 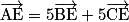 . Montrons que E appartient bien au plan (ABC).
. Montrons que E appartient bien au plan (ABC).
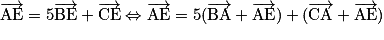 , en utilisant la relation de Chasles.
, en utilisant la relation de Chasles.
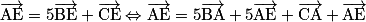
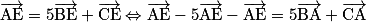
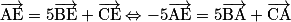
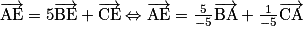
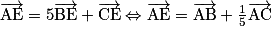
Ainsi E appartient au plan (ABC).
Remarque : La donnée d'un point et de deux vecteurs directeurs (non colinéaires) suffit à caractériser un plan.
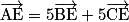 . Montrons que E appartient bien au plan (ABC).
. Montrons que E appartient bien au plan (ABC).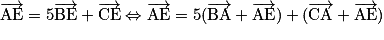 , en utilisant la relation de Chasles.
, en utilisant la relation de Chasles.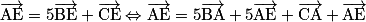
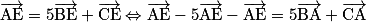
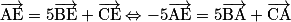
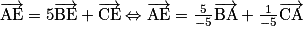
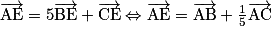
Ainsi E appartient au plan (ABC).
Remarque : La donnée d'un point et de deux vecteurs directeurs (non colinéaires) suffit à caractériser un plan.
IV. Que faut-il savoir sur la coplanarité ?
Des vecteurs coplanaires sont dits linéairement dépendants. On dit aussi qu'ils forment une famille liée.
Trois vecteurs non nuls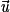 ,
, 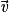 et
et 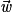 tels que
tels que 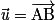 ,
, 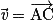 et
et 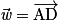 sont coplanaires si et seulement si A, B, C et D appartiennent au même plan (ABC). On dit alors que les points A, B, C et D sont coplanaires.
sont coplanaires si et seulement si A, B, C et D appartiennent au même plan (ABC). On dit alors que les points A, B, C et D sont coplanaires.
Exemple : Soit ABCDEFGH un pavé droit de centre O. On peut montrer que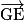 ,
, 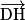 et
et 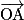 sont coplanaires.
sont coplanaires.
Propriétés : Soient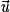 ,
, 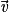 et
et 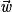 , trois vecteurs tels que
, trois vecteurs tels que 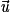 et
et 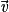 ne sont pas colinéaires.
ne sont pas colinéaires.
Trois vecteurs non nuls
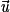 ,
, 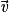 et
et 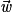 tels que
tels que 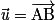 ,
, 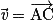 et
et 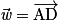 sont coplanaires si et seulement si A, B, C et D appartiennent au même plan (ABC). On dit alors que les points A, B, C et D sont coplanaires.
sont coplanaires si et seulement si A, B, C et D appartiennent au même plan (ABC). On dit alors que les points A, B, C et D sont coplanaires.Exemple : Soit ABCDEFGH un pavé droit de centre O. On peut montrer que
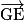 ,
, 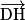 et
et 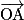 sont coplanaires.
sont coplanaires.Propriétés : Soient
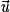 ,
, 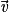 et
et 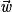 , trois vecteurs tels que
, trois vecteurs tels que 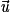 et
et 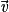 ne sont pas colinéaires.
ne sont pas colinéaires.• 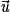 ,
, 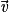 et
et 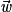 sont coplanaires si et seulement si
sont coplanaires si et seulement si 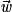 est égal à une combinaison linéaire de
est égal à une combinaison linéaire de 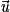 et
et 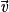 .
.
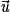 ,
, 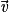 et
et 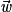 sont coplanaires si et seulement si
sont coplanaires si et seulement si 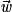 est égal à une combinaison linéaire de
est égal à une combinaison linéaire de 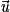 et
et 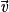 .
.• 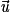 ,
, 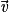 et
et 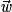 sont coplanaires si et seulement s'il existe trois réels a, b et c non tous nuls tels que
sont coplanaires si et seulement s'il existe trois réels a, b et c non tous nuls tels que 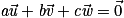 .
.
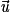 ,
, 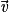 et
et 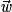 sont coplanaires si et seulement s'il existe trois réels a, b et c non tous nuls tels que
sont coplanaires si et seulement s'il existe trois réels a, b et c non tous nuls tels que 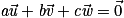 .
.• 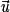 ,
, 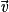 et
et 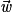 ne sont pas coplanaires si et seulement si
ne sont pas coplanaires si et seulement si 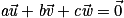 implique a = b = c = 0.
implique a = b = c = 0.
Des vecteurs non coplanaires sont dits linéairement indépendants. On dit aussi qu'ils forment une famille libre.
Exemple : Soit ABCD un tétraèdre avec I milieu de [AB]. Soient E tel que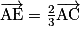 , F tel que
, F tel que 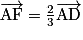 et G tel que GCBD parallélogramme. On peut montrer que
et G tel que GCBD parallélogramme. On peut montrer que 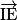 ,
, 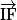 et
et 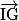 sont coplanaires.
sont coplanaires.
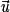 ,
, 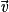 et
et 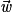 ne sont pas coplanaires si et seulement si
ne sont pas coplanaires si et seulement si 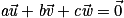 implique a = b = c = 0.
implique a = b = c = 0.Des vecteurs non coplanaires sont dits linéairement indépendants. On dit aussi qu'ils forment une famille libre.
Exemple : Soit ABCD un tétraèdre avec I milieu de [AB]. Soient E tel que
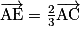 , F tel que
, F tel que 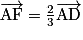 et G tel que GCBD parallélogramme. On peut montrer que
et G tel que GCBD parallélogramme. On peut montrer que 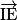 ,
, 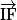 et
et 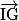 sont coplanaires.
sont coplanaires.V. Comment caractériser une base et un repère dans l'espace ?
Propriété : Soient 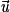 ,
, 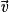 et
et 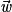 , trois vecteurs non colinéaires de l'espace. Quel que soit le vecteur
, trois vecteurs non colinéaires de l'espace. Quel que soit le vecteur 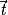 de l'espace, il est égal à une unique combinaison linéaire des vecteurs
de l'espace, il est égal à une unique combinaison linéaire des vecteurs 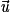 ,
, 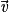 et
et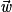 .
.
Exemples : Soit ABCDEFGH un cube.
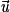 ,
, 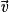 et
et 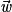 , trois vecteurs non colinéaires de l'espace. Quel que soit le vecteur
, trois vecteurs non colinéaires de l'espace. Quel que soit le vecteur 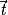 de l'espace, il est égal à une unique combinaison linéaire des vecteurs
de l'espace, il est égal à une unique combinaison linéaire des vecteurs 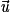 ,
, 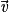 et
et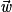 .
.Exemples : Soit ABCDEFGH un cube.
 |
• On peut exprimer de manière unique 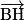 en fonction des vecteurs
en fonction des vecteurs 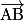 ,
, 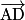 et
et 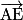 , car ces trois vecteurs ne sont pas colinéaires. En effet :
, car ces trois vecteurs ne sont pas colinéaires. En effet : 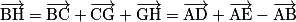 .
.
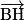 en fonction des vecteurs
en fonction des vecteurs 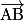 ,
, 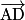 et
et 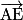 , car ces trois vecteurs ne sont pas colinéaires. En effet :
, car ces trois vecteurs ne sont pas colinéaires. En effet : 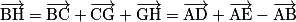 .
.• Soit I le milieu de [AB]. Le triplet 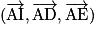 est une base de l'espace et
est une base de l'espace et 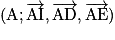 est un repère de l'espace.
est un repère de l'espace.
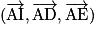 est une base de l'espace et
est une base de l'espace et 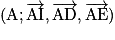 est un repère de l'espace.
est un repère de l'espace.VI. Comment étudier la position relative de deux droites dans l'espace ?
On étudie la position relative de deux droites dans l'espace : la droite D passant par A, de vecteur directeur 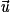 , et la droite D' passant par A', de vecteur directeur
, et la droite D' passant par A', de vecteur directeur 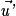 . Il suffit d'étudier leurs vecteurs directeurs.
. Il suffit d'étudier leurs vecteurs directeurs.
Si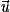 et
et 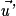 sont colinéaires, alors les droites D et D' sont parallèles. Deux cas sont alors possibles :
sont colinéaires, alors les droites D et D' sont parallèles. Deux cas sont alors possibles :
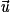 , et la droite D' passant par A', de vecteur directeur
, et la droite D' passant par A', de vecteur directeur 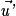 . Il suffit d'étudier leurs vecteurs directeurs.
. Il suffit d'étudier leurs vecteurs directeurs.Si
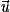 et
et 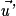 sont colinéaires, alors les droites D et D' sont parallèles. Deux cas sont alors possibles :
sont colinéaires, alors les droites D et D' sont parallèles. Deux cas sont alors possibles :• si A appartient à D', alors les droites D et D' sont confondues ;
• si A n'appartient pas à D', alors les droites D et D' sont strictement parallèles : leur intersection est vide.
Si 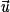 et
et 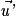 ne sont pas colinéaires, alors les droites D et D' sont soit sécantes (leur intersection est un point), soit non coplanaires (leur intersection est vide).
ne sont pas colinéaires, alors les droites D et D' sont soit sécantes (leur intersection est un point), soit non coplanaires (leur intersection est vide).
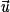 et
et 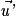 ne sont pas colinéaires, alors les droites D et D' sont soit sécantes (leur intersection est un point), soit non coplanaires (leur intersection est vide).
ne sont pas colinéaires, alors les droites D et D' sont soit sécantes (leur intersection est un point), soit non coplanaires (leur intersection est vide).VII. Comment étudier la position relative d'une droite et d'un plan ?
Propriété : Soit P un plan de vecteurs directeurs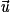 et
et 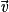 (non colinéaires), et D une droite de vecteur directeur
(non colinéaires), et D une droite de vecteur directeur 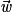 . P et D sont parallèles si et seulement si les vecteurs
. P et D sont parallèles si et seulement si les vecteurs 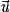 ,
, 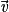 et
et 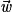 sont coplanaires.
sont coplanaires.Remarque : Si une droite et un plan ne sont pas parallèles, alors ils sont sécants en un point unique.
Cas particulier : Dans le cas où D et P sont parallèles, la droite D est incluse dans le plan P si et seulement si D et P admettent au moins un point commun.
VIII. Comment étudier la position relative de deux plans ?
Propriété : Deux plans P et Q sont parallèles si et seulement si P et Q admettent un même couple de vecteurs directeurs (non colinéaires).Remarque : Deux plans non parallèles sont sécants en une droite.
Cas particulier : Les deux plans P et Q sont confondus si et seulement si P et Q sont parallèles et possèdent au moins un point commun.
Histoire des mathématiques
Les concepts sous-jacents à la notion de vecteur apparaissent comme modèles pour la physique dynamique longtemps avant qu'ils ne soient formalisés mathématiquement.On trouve le concept de force dans les travaux d'Archimède (200 ans av. J.-C.), car il évoque le poids des corps sans pouvoir expliquer plus précisément l'hypothèse scientifique cachée derrière. La notion de force apparaît plus implicitement dans les travaux de Stevin au xvie siècle et est finalement formalisée par Newton au xviie siècle. C'est le premier qui donne une définition, encore utilisée aujourd'hui, qui permet de distinguer les notions de force et de vitesse. Ces deux notions sont encore présentes dans les calculs géométriques de Leibniz.
Au xixe siècle, la notion de vecteur va finalement émerger comme objet algébrique et géométrique, comme transformation, ou encore comme outil de repérage. Hamilton construit les vecteurs par une approche algébrique. Grassmann propose dans sa théorie des forces et des marées, en 1839, une approche géométrique qui étend à l'espace la notion de vecteurs et lui associe des règles de calcul algébrique (notamment un « produit linéaire » qui deviendra plus tard notre produit scalaire).
Enfin, des auteurs proches des mathématiques comme de la physique tels que Maxwell, Gibbs, Heaviside ou Peano, ont dégagé à la fin du xixe siècle de nouveaux principes du calcul vectoriel à trois dimensions ou plus, lui donnant une dimension dynamique tout en établissant une nouvelle structure : les espaces vectoriels.

