I. Que faut-il retenir sur les ensembles finis ?
Lorsque n est un entier naturel non nul, si E1, E2, …, En sont n ensembles finis deux à deux disjoints, on peut appliquer le principe additif : le nombre d'éléments de l'ensemble est égal à la somme du nombre d'éléments de chacun des ensembles E1, E2, …, En.
est égal à la somme du nombre d'éléments de chacun des ensembles E1, E2, …, En.Exemples : Soient E = {A ; S ; P} un ensemble fini contenant 3 éléments, et F l'ensemble fini des entiers de 5 (inclus) à 15 (inclus), contenant 11 éléments. Alors :
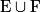 contient 3 + 11 = 14 éléments, car E et F sont deux ensembles finis et disjoints.
contient 3 + 11 = 14 éléments, car E et F sont deux ensembles finis et disjoints.Les parties de E sont : E (composé de 3 éléments) ; les sous-ensembles {A ; S}, {A ; P} et {S ; P} composés de 2 éléments chacun ; les sous-ensembles {A}, {S} et {P},composés de 1 élément chacun ; et l'ensemble vide.
Propriété : soit E un ensemble constitué de n éléments. Alors il existe 2n parties distinctes de E.
II. Qu'est-ce qu'une p-liste ?
Exemples : Soit E = {A ; S ; P}. On définit : F = (P ; S ; P ; P ; A). F est une 5-liste de E, c'est-à-dire une suite finie composée de 5 termes qui sont tous des éléments de E.Soit G =
 . Alors est une 2-liste de G (on dit aussi un couple de G). (2018 ; 2019 ; 2020) est une 3-liste de G (on dit aussi un triplet de G). Et on a :
. Alors est une 2-liste de G (on dit aussi un couple de G). (2018 ; 2019 ; 2020) est une 3-liste de G (on dit aussi un triplet de G). Et on a : 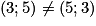 , car dans une p-liste, l'ordre dans lequel les éléments sont écrits est important (contrairement à un ensemble).
, car dans une p-liste, l'ordre dans lequel les éléments sont écrits est important (contrairement à un ensemble).On dit que a est la première composante du couple (a ; b), b la deuxième composante du couple. On dit que c est la troisième composante du triplet (a ; b ; c).
Notation : Soient E un ensemble fini et p un entier naturel non nul. L'ensemble des p-listes d'éléments de E se note Ep. Avec cette notation, E2 représente l'ensemble des couples d'éléments de E. On pose E1 = E.
Propriété : Soit E un ensemble fini possédant n éléments, soit
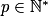 . Le nombre de p-listes d'éléments de E est égal à np.
. Le nombre de p-listes d'éléments de E est égal à np.Exemples : Soit E = {A ; S ; P}. Le nombre de 5-listes d'éléments de E est égal à 35 soit 243 5-listes différentes.
Pour composer un digicode, on utilise un clavier numérique contenant les dix chiffres 0, 1, …, 9), ainsi que les lettres A et B. Un code correct pour entrer dans l'immeuble est composé de 6 éléments. Il y a 126 6-listes différentes pour un digicode. Cela représente presque trois millions de codes différents à essayer pour entrer dans l'immeuble si on ne connaît pas le bon !
III. Que faut-il savoir sur le produit cartésien ?
Exemples : Soient E = {A ; S ; P} et F l'ensemble des entiers de 5 (inclus) à 15 (inclus). (A ; 6) est un couple du produit cartésien E × F.Soit G =
 . (2018 ; 2019 ; 2020) est un triplet de
. (2018 ; 2019 ; 2020) est un triplet de  3 =
3 =  ×
×  ×
×  .
.Lorsque n est un entier naturel non nul, si E1, E2, …, En sont n ensembles finis, on peut appliquer le principe multiplicatif : le nombre d'éléments du produit cartésien E1 × E2 × … × En est égal au produit du nombre d'éléments des ensembles E1, E2, …, En.
Exemple : Soient E l'ensemble {R ; D ; V ; 10 ; 9 ; 8 ; 7 ; As}, et F l'ensemble {Cœur ; Carreau ; Pique ; Trèfle}. Alors le produit cartésien E × F est un jeu classique de 32 cartes.
IV. Comment manipuler les arrangements ?
Exemples : Soit E = {s ; c ; o ; l ; a ; i ; r ; e}. (s, i, c) est un arrangement de trois éléments de E.
Soit F l'ensemble des entiers de 5 (inclus) à 15 (inclus). (5, 10, 7, 6) est un arrangement de quatre éléments de F, alors que (5, 10, 5, 6) n'est pas un arrangement de F, car 5 est écrit deux fois.
Propriété : Soit E un ensemble contenant n éléments, n étant un entier naturel non nul. Soit p un entier tel que 1 < p n. Le nombre d'arrangements de p éléments de E est égal à n × (n − 1) × (n − 2) × … × (n − (p − 1)).
n. Le nombre d'arrangements de p éléments de E est égal à n × (n − 1) × (n − 2) × … × (n − (p − 1)).
Remarques :
Soit F l'ensemble des entiers de 5 (inclus) à 15 (inclus). (5, 10, 7, 6) est un arrangement de quatre éléments de F, alors que (5, 10, 5, 6) n'est pas un arrangement de F, car 5 est écrit deux fois.
Propriété : Soit E un ensemble contenant n éléments, n étant un entier naturel non nul. Soit p un entier tel que 1 < p
 n. Le nombre d'arrangements de p éléments de E est égal à n × (n − 1) × (n − 2) × … × (n − (p − 1)).
n. Le nombre d'arrangements de p éléments de E est égal à n × (n − 1) × (n − 2) × … × (n − (p − 1)).Remarques :
• Le produit n × (n − 1) × (n − 2) × … × (n − (p − 1)) contient p facteurs.
• Lorsque p = 1, il y a n arrangements de 1 élément (singleton) de E.
V. Comment manipuler les permutations ?
Exemple : Soit E = {s ; c ; o ; l ; a ; i ; r ; e}. (s, i, c, o, l, a, e, r) est une permutation de E, mais pas (s, i, c, o, l, a, e, c) car l'élément c est répété.
Propriété : Le nombre de permutations de E est égal à n × (n − 1) × (n − 2) × … × 2 × 1.
Notation : le nombre n × (n − 1) × (n − 2) × … × 2 × 1 est noté n! et se lit « factorielle n ».
Exemple : 7 invités sont autour d'une table. Il existe 7! plans de table différents, soit 5 040 possibilités.
Propriété : Soit E un ensemble contenant n éléments, n étant un entier naturel non nul. Soit p un entier tel que 1 < p n. Le nombre d'arrangements de p éléments de E est égal à
n. Le nombre d'arrangements de p éléments de E est égal à 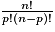 .
.
Programme : Voici un script en langage Python permettant de générer de manière aléatoire une permutation d'un ensemble entré sous la forme d'une liste.
Propriété : Le nombre de permutations de E est égal à n × (n − 1) × (n − 2) × … × 2 × 1.
Notation : le nombre n × (n − 1) × (n − 2) × … × 2 × 1 est noté n! et se lit « factorielle n ».
Exemple : 7 invités sont autour d'une table. Il existe 7! plans de table différents, soit 5 040 possibilités.
Propriété : Soit E un ensemble contenant n éléments, n étant un entier naturel non nul. Soit p un entier tel que 1 < p
 n. Le nombre d'arrangements de p éléments de E est égal à
n. Le nombre d'arrangements de p éléments de E est égal à 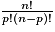 .
.Programme : Voici un script en langage Python permettant de générer de manière aléatoire une permutation d'un ensemble entré sous la forme d'une liste.
 |
Deux fonctions différentes sont proposées. Pour utiliser shuffle de la première fonction, il faut importer auparavant le module random à l'aide de la ligne : from random import.
VI. Comment manipuler les combinaisons ?
Exemple : Soit E = {s ; c ; o ; l ; a ; i ; r ; e}. F = {s, l, e} est une combinaison de 3 éléments de E. F = {e, s, l} en est également une. ø est la combinaison de zéro élément de E. E est la combinaison des 8 éléments de E.
Propriété : Soit E un ensemble contenant n éléments, n étant un entier naturel. Soit p un entier tel que 0 p
p  n. Le nombre de combinaisons de p éléments de E est égal à
n. Le nombre de combinaisons de p éléments de E est égal à 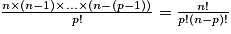 .
.
Notation : Ce nombre se note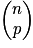 et se lit « p parmi n ». On dit aussi que c'est un coefficient binomial.
et se lit « p parmi n ». On dit aussi que c'est un coefficient binomial.
Remarque :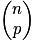 est égal au nombre de chemins représentant « p succès » lors de n répétitions d'une même épreuve de Bernoulli.
est égal au nombre de chemins représentant « p succès » lors de n répétitions d'une même épreuve de Bernoulli.
Exemple : En Belgique, le Lotto propose de choisir une grille de 6 numéros compris entre 1 et 45. Il y a donc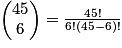 soit 8 145 060 grilles possibles !
soit 8 145 060 grilles possibles !
Cas particuliers : Soit E possédant n éléments, n étant un entier naturel.
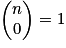 , car seul ø est une combinaison à 0 élément de E.
, car seul ø est une combinaison à 0 élément de E.
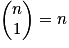 , car les parties à 1 élément de E sont les n singletons formés par les n éléments de E.
, car les parties à 1 élément de E sont les n singletons formés par les n éléments de E.
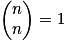 , car seul E est une combinaison à n éléments de E.
, car seul E est une combinaison à n éléments de E.
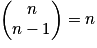 .
.
Propriétés : Symétrie :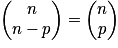 .
.
Relation de Pascal : soit p un entier tel que 0 < p < n, avec n entier naturel non nul :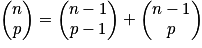 .
.
Démonstration de la relation de Pascal :
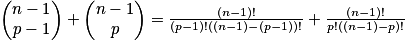
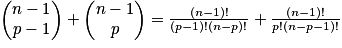
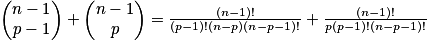
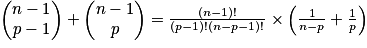
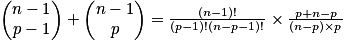
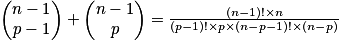
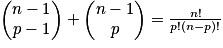
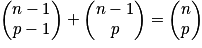
Triangle de Pascal
Propriété : Soit E un ensemble contenant n éléments, n étant un entier naturel. Soit p un entier tel que 0
 p
p  n. Le nombre de combinaisons de p éléments de E est égal à
n. Le nombre de combinaisons de p éléments de E est égal à 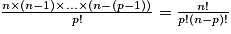 .
.Notation : Ce nombre se note
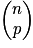 et se lit « p parmi n ». On dit aussi que c'est un coefficient binomial.
et se lit « p parmi n ». On dit aussi que c'est un coefficient binomial.Remarque :
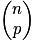 est égal au nombre de chemins représentant « p succès » lors de n répétitions d'une même épreuve de Bernoulli.
est égal au nombre de chemins représentant « p succès » lors de n répétitions d'une même épreuve de Bernoulli.Exemple : En Belgique, le Lotto propose de choisir une grille de 6 numéros compris entre 1 et 45. Il y a donc
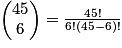 soit 8 145 060 grilles possibles !
soit 8 145 060 grilles possibles !Cas particuliers : Soit E possédant n éléments, n étant un entier naturel.
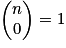 , car seul ø est une combinaison à 0 élément de E.
, car seul ø est une combinaison à 0 élément de E.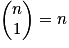 , car les parties à 1 élément de E sont les n singletons formés par les n éléments de E.
, car les parties à 1 élément de E sont les n singletons formés par les n éléments de E.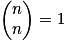 , car seul E est une combinaison à n éléments de E.
, car seul E est une combinaison à n éléments de E.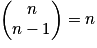 .
.Propriétés : Symétrie :
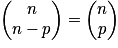 .
.Relation de Pascal : soit p un entier tel que 0 < p < n, avec n entier naturel non nul :
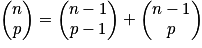 .
.Démonstration de la relation de Pascal :
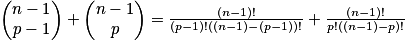
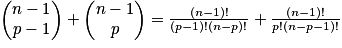
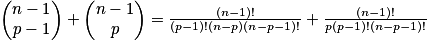
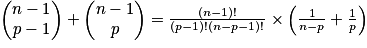
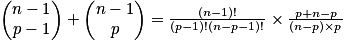
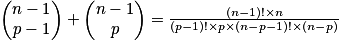
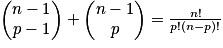
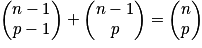
Triangle de Pascal
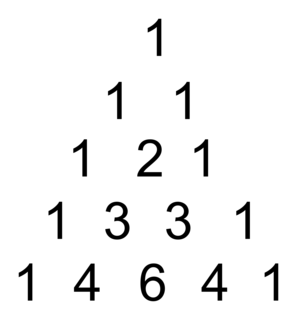 |
On retrouve dans ce triangle la valeur des nombres 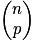 au niveau du pe élément sur la ne ligne (attention, la 1e ligne est numérotée 0).
au niveau du pe élément sur la ne ligne (attention, la 1e ligne est numérotée 0).
Par exemple :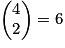 et
et 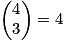 .
.
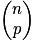 au niveau du pe élément sur la ne ligne (attention, la 1e ligne est numérotée 0).
au niveau du pe élément sur la ne ligne (attention, la 1e ligne est numérotée 0).Par exemple :
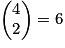 et
et 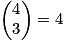 .
.Histoire des mathématiques
Des propriétés arithmétiques du triangle de Pascal étaient présentes dans les travaux combinatoires des mathématiques indiennes et chinoises.
• Entre 400 et 200 av. J.-C., en Inde, les jaïnistes introduisent les premiers concepts de cardinalité et de nombres transfinis, car ils sont persuadés que tous les nombres infinis ne sont pas égaux. L'école de Pingala parle déjà du système binaire et utilise le triangle de Pascal, même si cette notion sera redécouverte plus tard.
• Au moins 200 ans av. J.-C., les Chinois ont développé une sorte de numération en système binaire et des techniques arithmétiques qui leur permettaient de faire des calculs d'astronomie déjà très élaborés ou des recherches de carrés magiques (qui peuvent être utilisés dans les échecs, les jeux de cartes ou encore les dominos).
• Le triangle de Pascal apparaît réellement pour la première fois au Moyen-Orient au xxe siècle et en Chine au xiie siècle. Il servait alors à développer la formule du binôme : (a + b)n, ainsi qu'à généraliser à des degrés supérieurs à 2 la méthode d'extraction de la racine.
Pendant l'Antiquité, les calculs de combinatoire étaient des moments de prédilection lors des récréations mathématiques. La combinatoire est restée présente durant tous les siècles jusqu'aux arithméticiens du xixe siècle (Lucas, Delannoy, etc.).
Enfin, le développement de l'informatique et de l'intelligence artificielle s'est appuyé sur les « mathématiques discrètes » et les méthodes combinatoires pour exploiter ces nouvelles technologies au maximum.
Enfin, le développement de l'informatique et de l'intelligence artificielle s'est appuyé sur les « mathématiques discrètes » et les méthodes combinatoires pour exploiter ces nouvelles technologies au maximum.

