Énoncé
Exercice sur 5 points
L'espace est muni d'un repère orthonormé (O ; 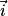 ,
, 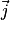 ,
, 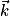 ).
).
On considère :
 ,
, 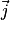 ,
, 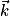 ).
).On considère :
• les points A(−1 ; 2 ; 1), B(1 ; −1 ; 2) et C(1 ; 1 ; 1) ;
• la droite d dont une représentation paramétrique est donnée par :
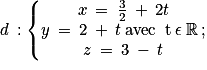
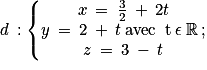
• la droite d' dont une représentation paramétrique est donnée par :
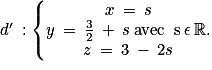
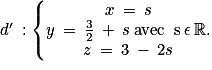
Partie A
1. Montrer que les droites d et d' sont sécantes au point 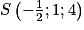 .
.
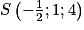 .
.2. a. Montrer que le vecteur 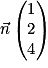 est un vecteur normal au plan (ABC).
est un vecteur normal au plan (ABC).
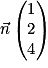 est un vecteur normal au plan (ABC).
est un vecteur normal au plan (ABC).b. En déduire qu'une équation cartésienne du plan (ABC) est :
x + 2y + 4z − 7 = 0
x + 2y + 4z − 7 = 0
c. Démontrer que les points A, B, C et S ne sont pas coplanaires.
3. a. Démontrer que le point H(−1 ; 0 ; 2) est le projeté orthogonal de S sur le plan (ABC).
b. En déduire qu'il n'existe aucun point M du plan (ABC) tel que 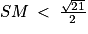 .
.
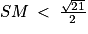 .
.Partie B
On considère un point M appartenant au segment [CS]. On a donc 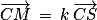 avec k réel de l'intervalle [0 ; 1].
avec k réel de l'intervalle [0 ; 1].
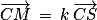 avec k réel de l'intervalle [0 ; 1].
avec k réel de l'intervalle [0 ; 1].1. Déterminer les coordonnées du point M en fonction de k.
2. Existe-t-il un point M sur le segment [CS] tel que le triangle MAB soit rectangle en M ?
Corrigé
Partie A
1. Le point S(xs ; ys ; zs) appartient à l'intersection des droites d et d' si et seulement si :
il existe 2 réels t et s tels que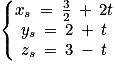 et
et 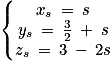 . On résout :
. On résout :
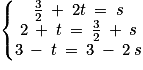
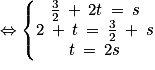
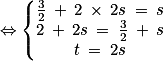
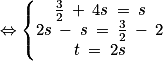
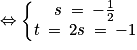
Ainsi, on a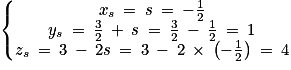 . Donc les droites d et d' sont bien sécantes en
. Donc les droites d et d' sont bien sécantes en 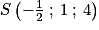 .
.
il existe 2 réels t et s tels que
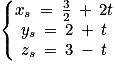 et
et 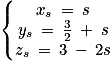 . On résout :
. On résout :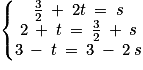
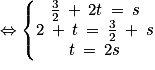
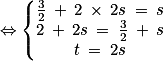
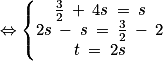
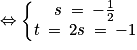
Ainsi, on a
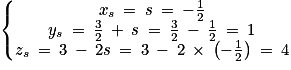 . Donc les droites d et d' sont bien sécantes en
. Donc les droites d et d' sont bien sécantes en 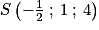 .
.Remarque : On peut aussi montrer que S appartient aux deux droites d et d'. Comme d et d' ne sont pas parallèles, puisque leurs coefficients directeurs (que l'on peut déterminer) ne sont pas colinéaires, alors cela signifie que d et d' sont bien sécantes en S.
2. a. Un vecteur est normal à un plan si et seulement le vecteur est orthogonal à deux vecteurs directeurs (non colinéaires) du plan.
Le plan (ABC) est dirigé (par exemple) par les vecteurs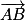 et
et 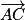 .
.
Déterminons les coordonnées de ces deux vecteurs.
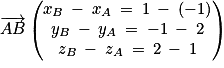 donc
donc 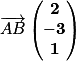
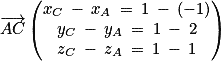 donc
donc 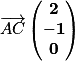
On constate que et
et  ne sont pas colinéaires (en effet, la dernière composante de
ne sont pas colinéaires (en effet, la dernière composante de 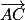 est 0 alors que la dernière composante de
est 0 alors que la dernière composante de 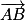 n'est pas nulle).
n'est pas nulle).
Le plan (ABC) est dirigé (par exemple) par les vecteurs
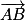 et
et 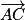 .
.Déterminons les coordonnées de ces deux vecteurs.
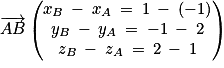 donc
donc 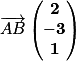
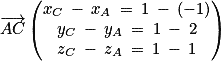 donc
donc 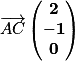
On constate que
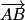 et
et 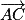 ne sont pas colinéaires (en effet, la dernière composante de
ne sont pas colinéaires (en effet, la dernière composante de 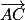 est 0 alors que la dernière composante de
est 0 alors que la dernière composante de 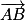 n'est pas nulle).
n'est pas nulle).Deux vecteurs non nuls sont orthogonaux si et seulement leur produit scalaire est nul.
On calcule donc le produit scalaire entre 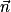 et
et 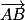 , puis entre
, puis entre 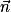 et
et  .
.
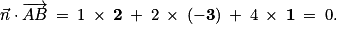
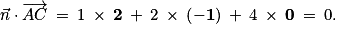
Ainsi, est orthogonal à
est orthogonal à  et à
et à 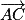 .
.
Donc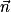 est un vecteur normal au plan (ABC).
est un vecteur normal au plan (ABC).
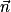 et
et 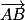 , puis entre
, puis entre 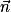 et
et 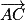 .
.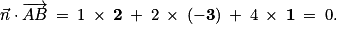
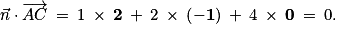
Ainsi,
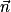 est orthogonal à
est orthogonal à 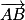 et à
et à 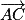 .
.Donc
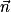 est un vecteur normal au plan (ABC).
est un vecteur normal au plan (ABC).b. Si 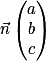 est un vecteur normal au plan P, alors une équation cartésienne de P est ax + by + cz + d = 0 avec d un réel à déterminer.
est un vecteur normal au plan P, alors une équation cartésienne de P est ax + by + cz + d = 0 avec d un réel à déterminer.
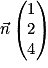 est un vecteur normal au plan (ABC), donc (ABC) : 1 × x + 2 × y + 4 × z + d = 0.
est un vecteur normal au plan (ABC), donc (ABC) : 1 × x + 2 × y + 4 × z + d = 0.
De plus, A(−1 ; 2 ; 1) appartient au plan (ABC) donc les coordonnées de A vérifie l'équation du plan.
On a donc :
1 × xA + 2 × yA + 4 × zA + d = 0
1 × (−1) + 2 × 2 + 4 × 1 + d = 0
7 + d = 0
d = −7
Ainsi :
(ABC) : 1 × x + 2 × y + 4 × z + (−7) = 0
Une équation cartésienne du plan (ABC) est donc x + 2y + 4z − 7 = 0
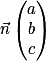 est un vecteur normal au plan P, alors une équation cartésienne de P est ax + by + cz + d = 0 avec d un réel à déterminer.
est un vecteur normal au plan P, alors une équation cartésienne de P est ax + by + cz + d = 0 avec d un réel à déterminer.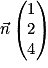 est un vecteur normal au plan (ABC), donc (ABC) : 1 × x + 2 × y + 4 × z + d = 0.
est un vecteur normal au plan (ABC), donc (ABC) : 1 × x + 2 × y + 4 × z + d = 0.De plus, A(−1 ; 2 ; 1) appartient au plan (ABC) donc les coordonnées de A vérifie l'équation du plan.
On a donc :
1 × xA + 2 × yA + 4 × zA + d = 0
1 × (−1) + 2 × 2 + 4 × 1 + d = 0
7 + d = 0
d = −7
Ainsi :
(ABC) : 1 × x + 2 × y + 4 × z + (−7) = 0
Une équation cartésienne du plan (ABC) est donc x + 2y + 4z − 7 = 0
c. Il suffit de montrer que le point S n'appartient pas au plan (ABC).
Calculons :
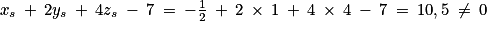
Donc les coordonnées de S ne vérifient pas l'équation du plan (ABC).
Donc, A, B, C et S ne sont pas coplanaires.
Calculons :
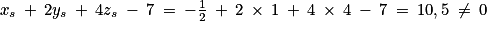
Donc les coordonnées de S ne vérifient pas l'équation du plan (ABC).
Donc, A, B, C et S ne sont pas coplanaires.
3. a. On montre que H appartient à (ABC) et que le vecteur 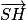 est un vecteur normal au plan (ABC).
est un vecteur normal au plan (ABC).
xH + 2yH + 4zH − 7 = −1 + 2 × 0 + 4 × 2 − 7 = 0
Donc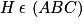 .
.
Et :
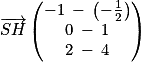
Donc :
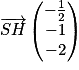
On constate que −2 ×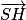 =
= 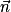 . Donc
. Donc 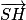 et
et 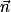 sont colinéaires. Or
sont colinéaires. Or 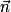 est normal à (ABC), donc
est normal à (ABC), donc 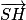 est également normal à (ABC).
est également normal à (ABC).
Ainsi H est le projeté orthogonal de S sur le plan (ABC).
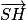 est un vecteur normal au plan (ABC).
est un vecteur normal au plan (ABC).xH + 2yH + 4zH − 7 = −1 + 2 × 0 + 4 × 2 − 7 = 0
Donc
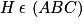 .
.Et :
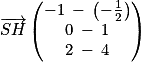
Donc :
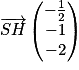
On constate que −2 ×
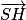 =
= 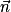 . Donc
. Donc 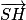 et
et 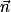 sont colinéaires. Or
sont colinéaires. Or 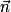 est normal à (ABC), donc
est normal à (ABC), donc 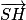 est également normal à (ABC).
est également normal à (ABC).Ainsi H est le projeté orthogonal de S sur le plan (ABC).
Remarque : Au lieu de montrer que 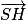 et
et 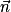 sont colinéaires, on peut montrer que
sont colinéaires, on peut montrer que 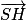 est orthogonal à
est orthogonal à 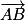 et
et 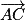 .
.
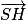 et
et 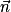 sont colinéaires, on peut montrer que
sont colinéaires, on peut montrer que 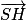 est orthogonal à
est orthogonal à 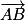 et
et 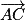 .
.b. La distance minimale entre le point S et tout point M du plan (ABC) est, par définition, la distance du point S au plan (ABC), c'est-à-dire la distance entre le point S et son projeté orthogonal sur le plan (ABC), soit ici H.
Donc, pour tout point M du plan (ABC), on a SM SH.
SH.
On peut calculer la longueur SH en calculant la norme du vecteur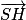 .
.
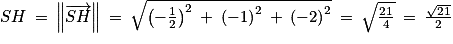
Donc, il n'existe pas de point M du plan (ABC) tel que SM <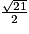 .
.
Donc, pour tout point M du plan (ABC), on a SM
 SH.
SH.On peut calculer la longueur SH en calculant la norme du vecteur
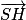 .
.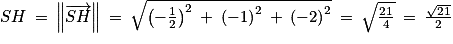
Donc, il n'existe pas de point M du plan (ABC) tel que SM <
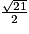 .
.Partie B
1. Soit le point M de coordonnées (xM ; yM ; zM).
On a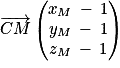 et
et 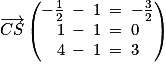
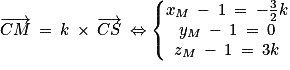
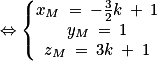
Donc le point M a pour coordonnées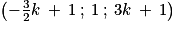 .
.
On a
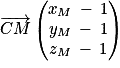 et
et 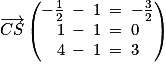
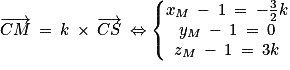
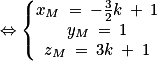
Donc le point M a pour coordonnées
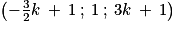 .
.2. MAB est un triangle rectangle en M si et seulement si 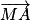 .
.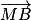 = 0.
= 0.
Or :
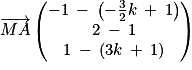 et
et 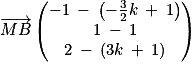
Donc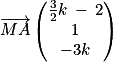 et
et 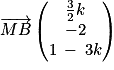
Donc le triangle MAB est un triangle rectangle en M
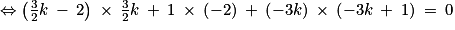
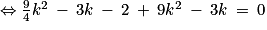
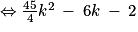
Soit Δ le discriminant de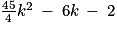 .
.
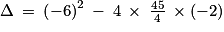
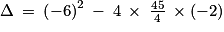
Δ = 126
Δ > 0 donc le polynôme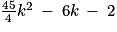 admet deux racines réelles :
admet deux racines réelles :
![k_{1}\: =\: \frac{-\left ( -6 \right )\: -\: \sqrt{126}}{2\: \times \: \frac{45}{4}}\: =\: \frac{6\: -\: \sqrt{126}}{22,5}\: \approx \: -0,232\: \notin \left [ 0\: ;\: 1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde37_m78.png)
![k_{2}\: =\: \frac{-\left ( -6 \right )\: +\: \sqrt{126}}{2\: \times \: \frac{45}{4}}\: =\: \frac{6\: +\: \sqrt{126}}{22,5}\: \approx \: 0,766\: \in \left [ 0\: ;\: 1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde37_m79.png)
Donc MAB est un triangle rectangle en M si et seulement si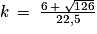 .
.
Il existe donc un unique point M du segment [CS] tel que MAB soit un triangle rectangle en M.
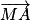 .
.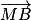 = 0.
= 0.Or :
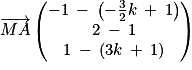 et
et 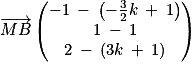
Donc
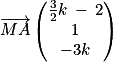 et
et 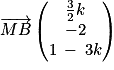
Donc le triangle MAB est un triangle rectangle en M
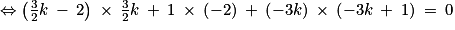
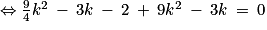
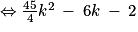
Soit Δ le discriminant de
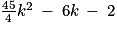 .
.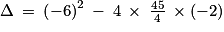
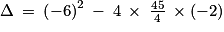
Δ = 126
Δ > 0 donc le polynôme
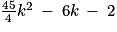 admet deux racines réelles :
admet deux racines réelles :![k_{1}\: =\: \frac{-\left ( -6 \right )\: -\: \sqrt{126}}{2\: \times \: \frac{45}{4}}\: =\: \frac{6\: -\: \sqrt{126}}{22,5}\: \approx \: -0,232\: \notin \left [ 0\: ;\: 1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde37_m78.png)
![k_{2}\: =\: \frac{-\left ( -6 \right )\: +\: \sqrt{126}}{2\: \times \: \frac{45}{4}}\: =\: \frac{6\: +\: \sqrt{126}}{22,5}\: \approx \: 0,766\: \in \left [ 0\: ;\: 1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde37_m79.png)
Donc MAB est un triangle rectangle en M si et seulement si
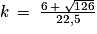 .
.Il existe donc un unique point M du segment [CS] tel que MAB soit un triangle rectangle en M.

