Sujet national, juin 2025, exercice 2

Énoncé

Exercice sur 5 points

L'espace est muni d'un repère orthonormé (O ; 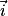$\vec{i}$ , $\vec{j}$ , $\vec{k}$ ).
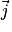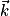On considère :

• les points A(−1 ; 2 ; 1), B(1 ; −1 ; 2) et C(1 ; 1 ; 1) ;

• la droite d dont une représentation paramétrique est donnée par :
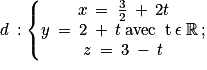
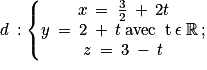
$d\: :\left\{\begin{matrix}x\: =\: \frac{3}{2}\: +\: 2t\\y\: =\: 2\: +\: t\: \textrm{avec\: t}\: \epsilon \: \mathbb{R}\: ;\\z\: =\: 3\: -\: t\end{matrix}\right.$

• la droite d' dont une représentation paramétrique est donnée par :
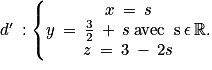
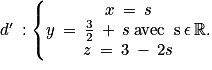
$d'\: :\left\{\begin{matrix}x\: =\: s\\y\: =\: \frac{3}{2}\: +\: s\: \textrm{avec\: s}\: \epsilon \: \mathbb{R}.\\z\: =\: 3\: -\: 2s\end{matrix}\right.$

Partie A

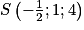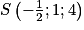1. Montrer que les droites d et d' sont sécantes au point $S\begin{pmatrix}-\frac{1}{2};1;4\end{pmatrix}$ .

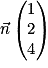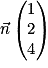2. a. Montrer que le vecteur $\vec{n}\begin{pmatrix}1\\2\\4\end{pmatrix}$ est un vecteur normal au plan (ABC).

b. En déduire qu'une équation cartésienne du plan (ABC) est :
x + 2y + 4z − 7 = 0

c. Démontrer que les points A, B, C et S ne sont pas coplanaires.

3. a. Démontrer que le point H(−1 ; 0 ; 2) est le projeté orthogonal de S sur le plan (ABC).

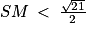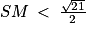b. En déduire qu'il n'existe aucun point M du plan (ABC) tel que $SM\: < \: \frac{\sqrt{21}}{2}$ .

Partie B

On considère un point M appartenant au segment [CS]. On a donc $\overrightarrow{CM}\: =\: k\: \overrightarrow{CS}$ avec k réel de l'intervalle [0 ; 1].

1. Déterminer les coordonnées du point M en fonction de k.

2. Existe-t-il un point M sur le segment [CS] tel que le triangle MAB soit rectangle en M ?

Corrigé

Partie A

1. Le point S(x_s ; y_s ; z_s) appartient à l'intersection des droites d et d' si et seulement si :
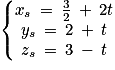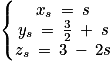il existe 2 réels t et s tels que $\left\{\begin{matrix}x_{s}\: =\: \frac{3}{2}\: +\: 2t\\y_{s}\: =\: 2\: +\: t\\z_{s}\: =\: 3\: -\: t\end{matrix}\right.$ et $\left\{\begin{matrix}x_{s}\: =\: s\\y_{s}\: =\: \frac{3}{2}\: +\: s\\z_{s}\: =\: 3\: -\: 2s\end{matrix}\right.$ . On résout :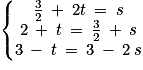
$\left\{\begin{matrix}\frac{3}{2}\: +\: 2t\: =\: s\\2\: +\: t\: =\: \frac{3}{2}\: +\: s\\3\: -\: t\: =\: 3\: -\: 2\: s\end{matrix}\right.$
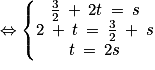
$\Leftrightarrow \left\{\begin{matrix}\frac{3}{2}\: +\: 2t\: =\: s\\2\: +\: t\: =\: \frac{3}{2}\: +\: s\\t\: =\: 2s\end{matrix}\right.$
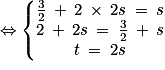
$\Leftrightarrow \left\{\begin{matrix}\frac{3}{2}\: +\: 2\: \times \: 2s\: =\: s\\2\: +\: 2s\: =\: \frac{3}{2}\: +\: s\\t\: =\: 2s\end{matrix}\right.$
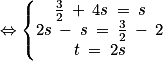
$\Leftrightarrow \left\{\begin{matrix}\frac{3}{2}\: +\: 4s\: =\: s\\2s\: -\: s\: =\: \frac{3}{2}\: -\: 2\\t\: =\: 2s\end{matrix}\right.$
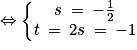
$\Leftrightarrow \left\{\begin{matrix}s\: =\: -\frac{1}{2}\\t\: =\: 2s\: =\: -1\end{matrix}\right.$
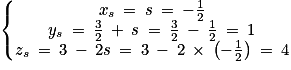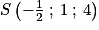Ainsi, on a $\left\{\begin{matrix}x_{s}\: =\: s\: =\: -\frac{1}{2}\\y_{s}\: =\: \frac{3}{2}\: +\: s\: =\: \frac{3}{2}\: -\: \frac{1}{2}\: =\: 1\\z_{s}\: =\: 3\: -\: 2s\: =\: 3\: -\: 2\: \times \: \left (-\frac{1}{2} \right )\: =\: 4\end{matrix}\right.$ . Donc les droites d et d' sont bien sécantes en $S\left ( -\frac{1}{2}\: ;\: 1\: ;\: 4 \right)$ .

Remarque : On peut aussi montrer que S appartient aux deux droites d et d'. Comme d et d' ne sont pas parallèles, puisque leurs coefficients directeurs (que l'on peut déterminer) ne sont pas colinéaires, alors cela signifie que d et d' sont bien sécantes en S.

2. a. Un vecteur est normal à un plan si et seulement le vecteur est orthogonal à deux vecteurs directeurs (non colinéaires) du plan.
Le plan (ABC) est dirigé (par exemple) par les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ .
Déterminons les coordonnées de ces deux vecteurs.
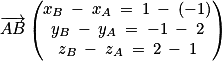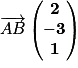
$\overrightarrow{AB}\begin{pmatrix}x_{B}\: -\: x_{A}\: =\: 1\: -\: \left ( -1 \right )\\y_{B}\: -\: y_{A}\: =\: -1\: -\: 2\\z_{B}\: -\: z_{A}\: =\: 2\: -\: 1\end{pmatrix}$ donc $\overrightarrow{AB}\begin{pmatrix}\mathbf{2}\\\mathbf{-3}\\\mathbf{1}\end{pmatrix}$
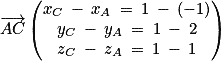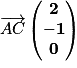
$\overrightarrow{AC}\begin{pmatrix}x_{C}\: -\: x_{A}\: =\: 1\: -\: \left ( -1 \right )\\y_{C}\: -\: y_{A}\: =\: 1\: -\: 2\\z_{C}\: -\: z_{A}\: =\: 1\: -\: 1\end{pmatrix}$ donc $\overrightarrow{AC}\begin{pmatrix}\mathbf{2}\\\mathbf{-1}\\\mathbf{0}\end{pmatrix}$
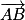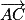On constate que $\overrightarrow{AB}$ et $\overrightarrow{AC}$ ne sont pas colinéaires (en effet, la dernière composante de 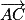$\overrightarrow{AC}$ est 0 alors que la dernière composante de 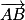$\overrightarrow{AB}$ n'est pas nulle).

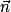Deux vecteurs non nuls sont orthogonaux si et seulement leur produit scalaire est nul.

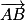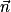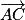On calcule donc le produit scalaire entre $\vec{n}$ et $\overrightarrow{AB}$ , puis entre $\vec{n}$ et $\overrightarrow{AC}$ .
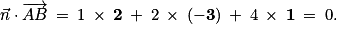
$\vec{n}\cdot \overrightarrow{AB}\: =\: 1\: \times \: \mathbf{2}\: +\: 2\: \times \: \left ( \mathbf{-3} \right )\: +\: 4\: \times \: \mathbf{1}\: =\: 0.$
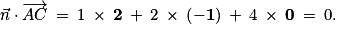
$\vec{n}\cdot \overrightarrow{AC}\: =\: 1\: \times \: \mathbf{2}\: +\: 2\: \times \: \left ( \mathbf{-1} \right )\: +\: 4\: \times \: \mathbf{0}\: =\: 0.$
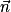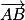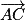Ainsi, $\vec{n}$ est orthogonal à $\overrightarrow{AB}$ et à $\overrightarrow{AC}$ .
Donc $\vec{n}$ est un vecteur normal au plan (ABC).

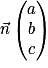b. Si $\vec{n}\begin{pmatrix}a\\b\\c\end{pmatrix}$ est un vecteur normal au plan P, alors une équation cartésienne de P est ax + by + cz + d = 0 avec d un réel à déterminer.
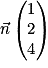$\vec{n}\begin{pmatrix}1\\2\\4\end{pmatrix}$ est un vecteur normal au plan (ABC), donc (ABC) : 1 × x + 2 × y + 4 × z + d = 0.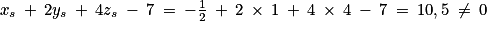
De plus, A(−1 ; 2 ; 1) appartient au plan (ABC) donc les coordonnées de A vérifie l'équation du plan.
On a donc :
1 × x_A + 2 × y_A + 4 × z_A + d = 0
1 × (−1) + 2 × 2 + 4 × 1 + d = 0
7 + d = 0
d = −7
Ainsi :
(ABC) : 1 × x + 2 × y + 4 × z + (−7) = 0
Une équation cartésienne du plan (ABC) est donc x + 2y + 4z − 7 = 0

c. Il suffit de montrer que le point S n'appartient pas au plan (ABC).
Calculons :
$x_{s}\: +\: 2y_{s}\: +\: 4z_{s}\: -\: 7\: =\: -\frac{1}{2}\: +\: 2\: \times \: 1\: +\: 4\: \times \: 4\: -\: 7\: =\: 10,5\: \neq \: 0$
Donc les coordonnées de S ne vérifient pas l'équation du plan (ABC).
Donc, A, B, C et S ne sont pas coplanaires.

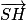3. a. On montre que H appartient à (ABC) et que le vecteur $\overrightarrow{SH}$ est un vecteur normal au plan (ABC).
x_H + 2y_H + 4z_H − 7 = −1 + 2 × 0 + 4 × 2 − 7 = 0
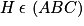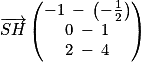
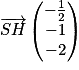
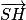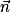Donc $H\: \epsilon \: \left ( ABC \right )$ .
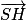Et :
$\overrightarrow{SH}\begin{pmatrix}-1\: -\: \left (- \frac{1}{2} \right )\\0\: -\: 1\\2\: -\: 4\end{pmatrix}$
Donc :
$\overrightarrow{SH}\begin{pmatrix}-\frac{1}{2}\\-1\\-2\end{pmatrix}$
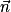On constate que −2 × $\overrightarrow{SH}$ = $\vec{n}$ . Donc $\overrightarrow{SH}$ et $\vec{n}$ sont colinéaires. Or 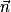$\vec{n}$ est normal à (ABC), donc 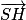$\overrightarrow{SH}$ est également normal à (ABC).
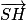Ainsi H est le projeté orthogonal de S sur le plan (ABC).

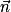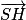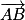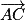Remarque : Au lieu de montrer que $\overrightarrow{SH}$ et $\vec{n}$ sont colinéaires, on peut montrer que $\overrightarrow{SH}$ est orthogonal à $\overrightarrow{AB}$ et $\overrightarrow{AC}$ .

b. La distance minimale entre le point S et tout point M du plan (ABC) est, par définition, la distance du point S au plan (ABC), c'est-à-dire la distance entre le point S et son projeté orthogonal sur le plan (ABC), soit ici H.
Donc, pour tout point M du plan (ABC), on a SM supérieur ou égal

SH.
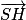On peut calculer la longueur SH en calculant la norme du vecteur $\overrightarrow{SH}$ .
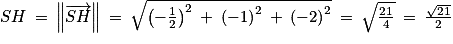
$SH\: =\: \left\| \overrightarrow{SH}\right\| \: =\: \sqrt{\left ( -\frac{1}{2} \right )^{2}\: +\: \left ( -1 \right )^{2}\: +\: \left ( -2 \right )^{2}}\: =\: \sqrt{\frac{21}{4}}\: =\: \frac{\sqrt{21}}{2}$
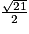Donc, il n'existe pas de point M du plan (ABC) tel que SM < $\frac{\sqrt{21}}{2}$ .

Partie B

1. Soit le point M de coordonnées (x_M ; y_M ; z_M).
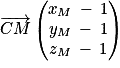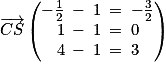
On a $\overrightarrow{CM}\begin{pmatrix}x_{M}\: -\: 1\\y_{M}\: -\: 1\\z_{M}\: -\: 1\end{pmatrix}$ et $\overrightarrow{CS}\begin{pmatrix}-\frac{1}{2}\: -\: 1\: =\: -\frac{3}{2}\\1\: -\: 1\: =\: 0\\4\: -\: 1\: =\: 3\end{pmatrix}$
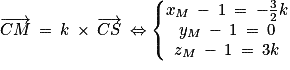
$\overrightarrow{CM}\: =\: k\: \times \: \overrightarrow{CS}\: \Leftrightarrow \left\{\begin{matrix}x_{M}\: -\: 1\: =\: -\frac{3}{2}k\\y_{M}\: -\: 1\: =\: 0\\z_{M}\: -\: 1\: =\: 3k\end{matrix}\right.$
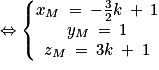
$\Leftrightarrow \left\{\begin{matrix}x_{M}\: =\: -\frac{3}{2}k\: +\: 1\\y_{M}\: =\: 1\\z_{M}\: =\: 3k\: +\: 1\end{matrix}\right.$
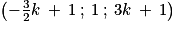Donc le point M a pour coordonnées $\left ( -\frac{3}{2}k\: +\: 1\: ;\: 1\: ;\: 3k\: +\: 1 \right )$ .

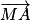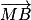2. MAB est un triangle rectangle en M si et seulement si $\overrightarrow{MA}$ . $\overrightarrow{MB}$ = 0.
Or :
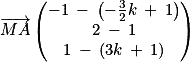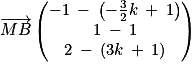
$\overrightarrow{MA}\begin{pmatrix}-1\: -\: \left ( -\frac{3}{2}k\: +\: 1 \right )\\2\: -\: 1\\1\: -\: \left ( 3k\: +\: 1 \right )\end{pmatrix}$ et $\overrightarrow{MB}\begin{pmatrix}-1\: -\: \left ( -\frac{3}{2}k\: +\: 1 \right )\\1\: -\: 1\\2\: -\: \left ( 3k\: +\: 1 \right )\end{pmatrix}$
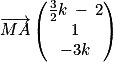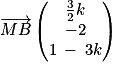
Donc $\overrightarrow{MA}\begin{pmatrix}\frac{3}{2}k\: -\: 2\\1\\-3k\end{pmatrix}$ et $\overrightarrow{MB}\begin{pmatrix}\frac{3}{2}k\\-2\\1\: -\: 3k\end{pmatrix}$
Donc le triangle MAB est un triangle rectangle en M
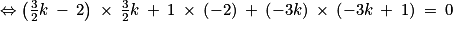
$\Leftrightarrow \left (\frac{3}{2}k\: -\: 2 \right )\: \times \: \frac{3}{2}k\: +\: 1\: \times \: \left ( -2 \right )\: +\: \left ( -3k \right )\: \times \: \left ( -3k\: +\: 1 \right )\: =\: 0$
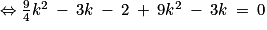
$\Leftrightarrow\frac{9}{4}k^{2}\: -\: 3k\: -\: 2\: +\: 9k^{2}\: -\: 3k\: =\: 0$
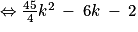
$\Leftrightarrow\frac{45}{4}k^{2}\: -\: 6k\: -\: 2$
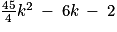Soit Δ le discriminant de $\frac{45}{4}k^{2}\: -\: 6k\: -\: 2$ .
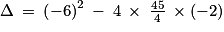
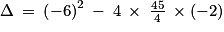
$\Delta \: =\: \left ( -6 \right )^{2}\: -\: 4\: \times \: \frac{45}{4}\: \times \left ( -2 \right )$
$\Delta \: =\: \left ( -6 \right )^{2}\: -\: 4\: \times \: \frac{45}{4}\: \times \left ( -2 \right )$
Δ = 126
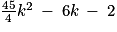Δ > 0 donc le polynôme $\frac{45}{4}k^{2}\: -\: 6k\: -\: 2$ admet deux racines réelles :
$k_{1}\: =\: \frac{-\left ( -6 \right )\: -\: \sqrt{126}}{2\: \times \: \frac{45}{4}}\: =\: \frac{6\: -\: \sqrt{126}}{22,5}\: \approx \: -0,232\: \notin \left [ 0\: ;\: 1 \right ]$
$k_{2}\: =\: \frac{-\left ( -6 \right )\: +\: \sqrt{126}}{2\: \times \: \frac{45}{4}}\: =\: \frac{6\: +\: \sqrt{126}}{22,5}\: \approx \: 0,766\: \in \left [ 0\: ;\: 1 \right ]$
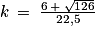Donc MAB est un triangle rectangle en M si et seulement si $k\: =\: \frac{6\: +\: \sqrt{126}}{22,5}$ .
Il existe donc un unique point M du segment [CS] tel que MAB soit un triangle rectangle en M.

Sujet national, juin 2025, exercice 2

Énoncé

Partie A

Partie B

Annexes

Corrigé

Partie A

Partie B