Énoncé
Exercice sur 5 points
Une entreprise a créé une foire aux questions (« FAQ ») sur son site internet.On étudie le nombre de questions qui y sont posées chaque mois.
Partie A : Première modélisation
Dans cette partie, on admet que chaque mois :
• 90 % des questions déjà posées le mois précédent sont conservées sur la FAQ ;
• 130 nouvelles questions sont ajoutées à la FAQ.
Au cours du premier mois, 300 questions ont été posées.
Pour estimer le nombre de questions, en centaines, présentes sur la FAQ le n-ième mis, on modélise la situation ci-dessus à l'aide de la suite (un) définie par :
u1 = 3 et, pour tout entier naturel n 1, un+1 = 0,9un + 1,3.
1, un+1 = 0,9un + 1,3.
Pour estimer le nombre de questions, en centaines, présentes sur la FAQ le n-ième mis, on modélise la situation ci-dessus à l'aide de la suite (un) définie par :
u1 = 3 et, pour tout entier naturel n
 1, un+1 = 0,9un + 1,3.
1, un+1 = 0,9un + 1,3.1. Calculer u2 et u3, et proposer une interprétation dans le contexte de l'exercice.
2. Montrer par récurrence que pour tout entier naturel 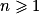 :
:
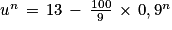
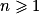 :
: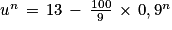
3. En déduire que la suite (un) est croissante.
4. On considère le programme ci-dessous, écrit en langage Python.
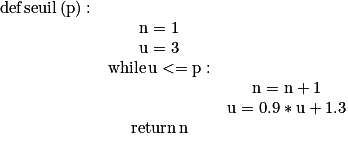
Déterminer la valeur renvoyée par la saisie de seuil(8.5) et l'interpréter dans le contexte de l'exercice.
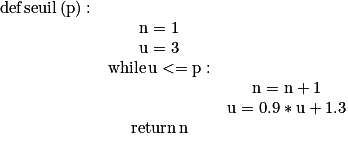
Déterminer la valeur renvoyée par la saisie de seuil(8.5) et l'interpréter dans le contexte de l'exercice.
Partie B : Une autre modélisation
Dans cette partie, on considère une seconde modélisation à l'aide d'une nouvelle suite (vn) définie pour tout entier naturel n  1 par :
1 par :
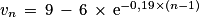
Le terme vu est une estimation du nombre de questions, en centaines, présentes le n-ième mois sur la FAQ.
 1 par :
1 par :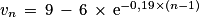
Le terme vu est une estimation du nombre de questions, en centaines, présentes le n-ième mois sur la FAQ.
1. Préciser les valeurs arrondies au centième de v1 et v2.
2. Déterminer, en justifiant la réponse, la plus petite valeur de n telle que vn> 8,5.
Partie C : Comparaison des deux modèles
1. L'entreprise considère qu'elle doit modifier la présentation de son site lorsque plus de 850 questions sont présentes sur la FAQ. Parmi ces deux modélisations, laquelle conduit à procéder le plus tôt à cette modification ? Justifier votre réponse.
2. En justifiant la réponse, pour quelle modélisation y a-t-il le plus grand nombre de questions sur la FAQ à long terme ?
Corrigé
Partie A : Première modélisation
1. On a la propriété suivante :
Pour tout entier naturel n supérieur ou égal à 1 : un+1 = 0,9 × un + 1,3.
Cette propriété est donc vraie en particulier lorsque n = 1. Cela donne l'égalité suivante :
u1+1 = 0,9 × u1 + 1,3
u2 = 0,9 × 3 + 1,3 = 2,7 + 1,3 = 4
La propriété est également vraie lorsque n=2. Cela donne :
u2+1 = 0,9 × u 2 + 1,3
u3 = 0,9×4 + 1,3 = 3,6 + 1,3 = 4,9
Or pour tout entier naturel n supérieur ou égal à 1 : unest le nombre de questions, en centaines, présentes sur la FAQ le n-ième mois.
Cela signifie donc qu'il y a eu 4 centaines de questions le deuxième mois. Il y a eu 4,9 centaines, soit 490 questions, le troisième mois.
Pour tout entier naturel n supérieur ou égal à 1 : un+1 = 0,9 × un + 1,3.
Cette propriété est donc vraie en particulier lorsque n = 1. Cela donne l'égalité suivante :
u1+1 = 0,9 × u1 + 1,3
u2 = 0,9 × 3 + 1,3 = 2,7 + 1,3 = 4
La propriété est également vraie lorsque n=2. Cela donne :
u2+1 = 0,9 × u 2 + 1,3
u3 = 0,9×4 + 1,3 = 3,6 + 1,3 = 4,9
Or pour tout entier naturel n supérieur ou égal à 1 : unest le nombre de questions, en centaines, présentes sur la FAQ le n-ième mois.
Cela signifie donc qu'il y a eu 4 centaines de questions le deuxième mois. Il y a eu 4,9 centaines, soit 490 questions, le troisième mois.
2. On souhaite prouver à l'aide d'une démonstration par récurrence la propriété suivante :
Pour tout entier n supérieur ou égal à 1 :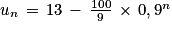 .
.
Initialisation : on vérifie que la propriété est vraie lorsque n = 1.
D'une part on sait que : u1 = 3.
D'autre part on a :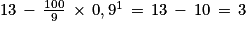 .
.
On a bien :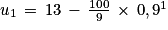 .
.
La propriété est donc vraie lorsque n = 1.
Hypothèse de récurrence :
On suppose qu'il existe un entier naturel n non nul tel que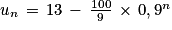 .
.
Preuve de l'hérédité :
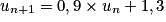
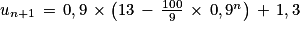
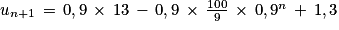
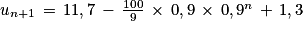
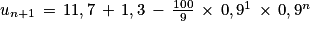
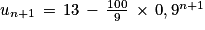
Ainsi, on a prouvé que si la propriété est vraie pour un entier naturel n quelconque alors elle est également vraie pour l'entier n + 1.
Ainsi, par récurrence :
Pour tout entier naturel n supérieur ou égal à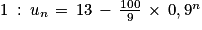 .
.
Pour tout entier n supérieur ou égal à 1 :
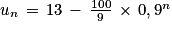 .
.Initialisation : on vérifie que la propriété est vraie lorsque n = 1.
D'une part on sait que : u1 = 3.
D'autre part on a :
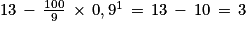 .
.On a bien :
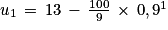 .
.La propriété est donc vraie lorsque n = 1.
Hypothèse de récurrence :
On suppose qu'il existe un entier naturel n non nul tel que
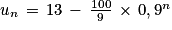 .
.Preuve de l'hérédité :
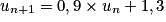
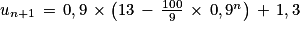
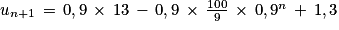
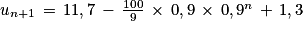
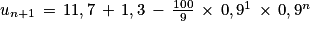
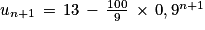
Ainsi, on a prouvé que si la propriété est vraie pour un entier naturel n quelconque alors elle est également vraie pour l'entier n + 1.
Ainsi, par récurrence :
Pour tout entier naturel n supérieur ou égal à
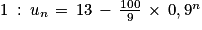 .
.3. Pour déterminer le sens de variation de la suite (un), la méthode choisie ici consiste à étudier le signe de la différence un+1−un.
Pour tout entier naturel n non nul :
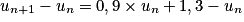
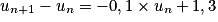
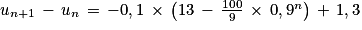
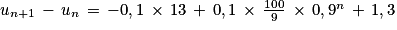
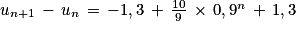
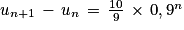
Or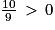 et pour tout entier naturel n non nul : 0,9n > 0.
et pour tout entier naturel n non nul : 0,9n > 0.
Ainsi, pour tout entier naturel n non nul : un+1 − un > 0.
Ainsi la suite (un) est strictement croissante.
On peut aussi affirmer que la suite (un) est croissante car pour tout entier naturel n non nul : un+1 − un 0. En effet 0
0. En effet 0  0.
0.
Pour tout entier naturel n non nul :
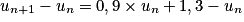
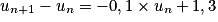
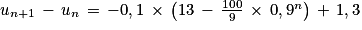
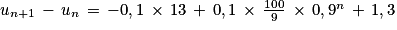
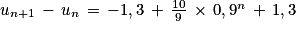
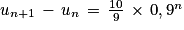
Or
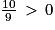 et pour tout entier naturel n non nul : 0,9n > 0.
et pour tout entier naturel n non nul : 0,9n > 0.Ainsi, pour tout entier naturel n non nul : un+1 − un > 0.
Ainsi la suite (un) est strictement croissante.
On peut aussi affirmer que la suite (un) est croissante car pour tout entier naturel n non nul : un+1 − un
 0. En effet 0
0. En effet 0  0.
0.4. On a fixé p = 8,5
Initialisation des valeurs n et u au début : n = 1 et u = 3.
La boucle non bornée while (ou « Tant que ») démarre et effectue le test suivant : est-il vrai ou faux d'affirmer que u est inférieur ou égal à p ?
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| u | 3 | 4 | 4,9 | 5,71 | 6,439 | 7,0951 | 7,68559 | 8,217031 | 8,6953279 |
u  p p | vrai | vrai | vrai | vrai | vrai | vrai | vrai | vrai | faux |
Initialisation des valeurs n et u au début : n = 1 et u = 3.
La boucle non bornée while (ou « Tant que ») démarre et effectue le test suivant : est-il vrai ou faux d'affirmer que u est inférieur ou égal à p ?
• Si la réponse est « vrai » alors les valeurs de n et u sont modifiées (n devient son ancienne valeur incrémentée de 1, et u devient son ancienne valeur multipliée par 0,9 puis augmentée de 1,3).
• Si la réponse est « faux » alors la boucle est terminée, et la valeur finale retournée dans la console sera la dernière valeur en mémoire de n.
Ainsi, ici, après avoir « tourné » 8 fois, la boucle s'arrête. La dernière valeur en mémoire de n est 9. C'est la valeur renvoyée par la saisie de seuil(8.5).
Dans le contexte de l'exercice, le test u p correspond à un
p correspond à un p.
p.
La boucle signifie donc « Tant que le terme unest inférieur au nombre p alors… »
Ainsi la valeur finale de n en mémoire correspond à l'indice du premier terme de la suite (un) qui ne vérifie pas le test, c'est-à-dire qui est strictement supérieur au nombre p.
Cela signifie que le plus petit entier tel que un > 8,5 est n = 9.
Or pour tout entier naturel n supérieur ou égal à 1 : unest le nombre de questions, en centaines, présentes sur la FAQ le n-ième mois.
Donc c'est à partir du neuvième mois que le nombre de questions sera strictement supérieur à 8,5 centaines (ou 850 questions). Il sera en effet ce mois-là d'environ 869, alors qu'au mois précédent il était d'environ 822.
Dans le contexte de l'exercice, le test u
 p correspond à un
p correspond à un p.
p.La boucle signifie donc « Tant que le terme unest inférieur au nombre p alors… »
Ainsi la valeur finale de n en mémoire correspond à l'indice du premier terme de la suite (un) qui ne vérifie pas le test, c'est-à-dire qui est strictement supérieur au nombre p.
Cela signifie que le plus petit entier tel que un > 8,5 est n = 9.
Or pour tout entier naturel n supérieur ou égal à 1 : unest le nombre de questions, en centaines, présentes sur la FAQ le n-ième mois.
Donc c'est à partir du neuvième mois que le nombre de questions sera strictement supérieur à 8,5 centaines (ou 850 questions). Il sera en effet ce mois-là d'environ 869, alors qu'au mois précédent il était d'environ 822.
Partie B : Une autre modélisation
1. Pour tout entier naturel non nul n : 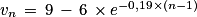
Donc en particulier lorsque n=1, on a :
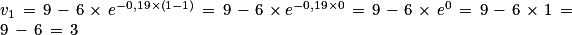
Et lorsque n=2, on a :
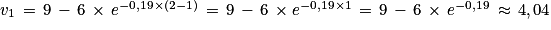
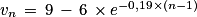
Donc en particulier lorsque n=1, on a :
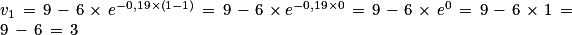
Et lorsque n=2, on a :
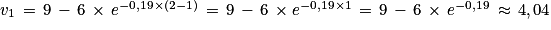
2. On cherche le plus petit entier naturel n non nul tel que :
vn > 8,5
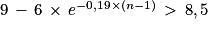
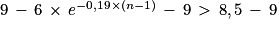
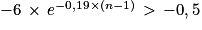
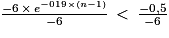
(on a divisé les deux membres de l'inégalité par un nombre strictement négatif)
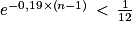
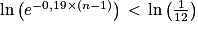
(la fonction logarithme népérien est strictement croissante sur![\left ]0\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde30_m32.png) )
)
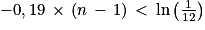
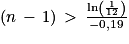
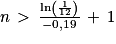
Or
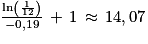
Ainsi le plus petit entier naturel n, tel que vn < 8,5, est l'entier 15.
On pouvait aussi observer les valeurs des premiers termes de la suite (vn). À l'aide de la calculatrice cela est très rapide. En particulier, on conjecture que (vn) est croissante et que v14 < 8,5 < v15.
vn > 8,5
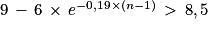
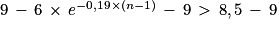
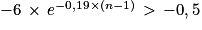
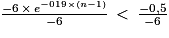
(on a divisé les deux membres de l'inégalité par un nombre strictement négatif)
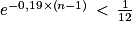
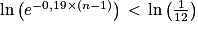
(la fonction logarithme népérien est strictement croissante sur
![\left ]0\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde30_m32.png) )
)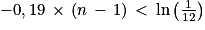
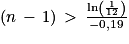
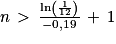
Or
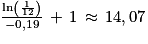
Ainsi le plus petit entier naturel n, tel que vn < 8,5, est l'entier 15.
On pouvait aussi observer les valeurs des premiers termes de la suite (vn). À l'aide de la calculatrice cela est très rapide. En particulier, on conjecture que (vn) est croissante et que v14 < 8,5 < v15.
Partie C : Comparaison des deux modèles
1. La première modélisation indique que le plus petit entier naturel n tel que un > 8,5 est n0 = 9.
La seconde modélisation indique que le plus petit entier naturel n tel que vn>8,5 est n1 = 15.
Comme n0 < n1, c'est donc la première modélisation qui conduirait à procéder le plus tôt à la modification de présentation du site de l'entreprise.
La seconde modélisation indique que le plus petit entier naturel n tel que vn>8,5 est n1 = 15.
Comme n0 < n1, c'est donc la première modélisation qui conduirait à procéder le plus tôt à la modification de présentation du site de l'entreprise.
2. D'une part :
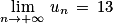
En effet, comme 0 < 0,9 < 1 :
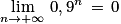
Par produit :
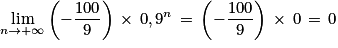
Et par somme :
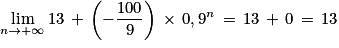
D'autre part :
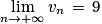
En effet :
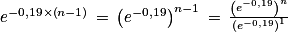
Comme 0 < e−0,19<1 :
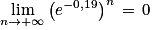
Par quotient :
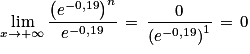
Donc à long terme le nombre de questions va se stabiliser vers 13 centaines de questions selon la première modélisation, et vers 9 centaines de questions selon la seconde modélisation.
Donc, c'est pour la première modélisation qu'il y aurait le plus grand nombre de questions sur la FAQ à long terme.
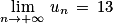
En effet, comme 0 < 0,9 < 1 :
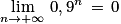
Par produit :
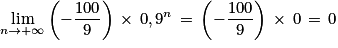
Et par somme :
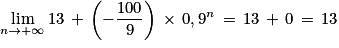
D'autre part :
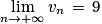
En effet :
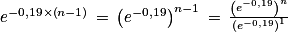
Comme 0 < e−0,19<1 :
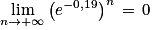
Par quotient :
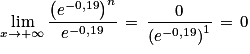
Donc à long terme le nombre de questions va se stabiliser vers 13 centaines de questions selon la première modélisation, et vers 9 centaines de questions selon la seconde modélisation.
Donc, c'est pour la première modélisation qu'il y aurait le plus grand nombre de questions sur la FAQ à long terme.

