Énoncé
Exercice sur 5 points
On considère la fonction f définie sur ]0 ; 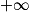 [ par f(x) = x2 − 8 ln(x), où ln désigne la fonction logarithme népérien.
[ par f(x) = x2 − 8 ln(x), où ln désigne la fonction logarithme népérien.
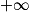 [ par f(x) = x2 − 8 ln(x), où ln désigne la fonction logarithme népérien.
[ par f(x) = x2 − 8 ln(x), où ln désigne la fonction logarithme népérien.On admet que f est dérivable sur ]0 ; 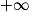 [, on note
[, on note 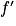 sa fonction dérivée.
sa fonction dérivée.
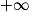 [, on note
[, on note 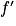 sa fonction dérivée.
sa fonction dérivée.1. Déterminer limx→0 f(x).
2. On admet que, pour tout x > 0, f(x) = x2(1 − 8 ln(x)x2).
En déduire la limite : limx→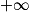 f(x).
f(x).
En déduire la limite : limx→
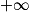 f(x).
f(x).3. Montrer que, pour tout réel x de ]0 ; 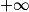 [,
[, 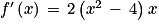 .
.
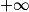 [,
[, 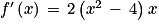 .
.4. Étudier les variations de f sur ]0 ; 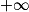 [ et dresser son tableau de variations complet.
[ et dresser son tableau de variations complet.
On précisera la valeur exacte du minimum de f sur ]0 ;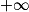 [.
[.
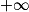 [ et dresser son tableau de variations complet.
[ et dresser son tableau de variations complet.On précisera la valeur exacte du minimum de f sur ]0 ;
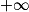 [.
[.5. Démontrer que, sur l'intervalle ]0 ; 2], l'équation f(x) = 0 admet une solution unique α (on ne cherchera pas à déterminer la valeur de α).
6. On admet que, sur l'intervalle [2 ; 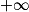 [, l'équation f(x) = 0 admet une solution unique β (on ne cherchera pas à déterminer la valeur de β).
[, l'équation f(x) = 0 admet une solution unique β (on ne cherchera pas à déterminer la valeur de β).
En déduire le signe de f sur l'intervalle ]0 ;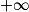 [.
[.
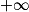 [, l'équation f(x) = 0 admet une solution unique β (on ne cherchera pas à déterminer la valeur de β).
[, l'équation f(x) = 0 admet une solution unique β (on ne cherchera pas à déterminer la valeur de β).En déduire le signe de f sur l'intervalle ]0 ;
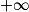 [.
[.7. Pour tout nombre réel k, on considère la fonction gk définie sur ]0 ; 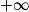 [ par :gk(x) = x2 − 8ln(x) + k
[ par :gk(x) = x2 − 8ln(x) + k
En s'aidant du tableau de variations de f, déterminer la plus petite valeur de k pour laquelle la fonction gk est positive sur l'intervalle ]0 ;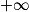 [.
[.
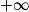 [ par :gk(x) = x2 − 8ln(x) + k
[ par :gk(x) = x2 − 8ln(x) + kEn s'aidant du tableau de variations de f, déterminer la plus petite valeur de k pour laquelle la fonction gk est positive sur l'intervalle ]0 ;
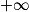 [.
[.Corrigé
1. D'une part :
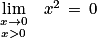
D'autre part :
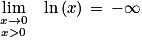
Donc par produit :
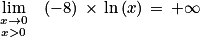
Ainsi par somme :
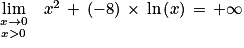
Donc :
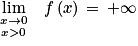
(Graphiquement, la droite d'équation x = 0, c'est-à-dire l'axe des ordonnées du repère, est une asymptote « verticale » à la courbe représentative de la fonction f).
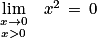
D'autre part :
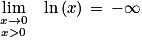
Donc par produit :
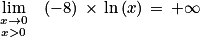
Ainsi par somme :
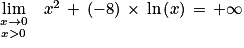
Donc :
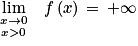
(Graphiquement, la droite d'équation x = 0, c'est-à-dire l'axe des ordonnées du repère, est une asymptote « verticale » à la courbe représentative de la fonction f).
2. D'après la propriété des croissances comparées, on a :
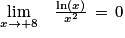
(On dit de manière familière qu'une fonction puissance « l'emporte » sur la fonction logarithme népérien lorsque x tend vers ).
).
Ainsi, par produit, on a :
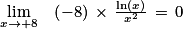
Par somme, on a :
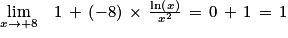
De plus :
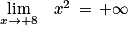
Ainsi par produit :
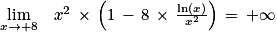
Donc :
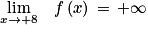
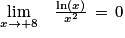
(On dit de manière familière qu'une fonction puissance « l'emporte » sur la fonction logarithme népérien lorsque x tend vers
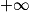 ).
).Ainsi, par produit, on a :
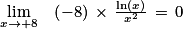
Par somme, on a :
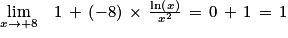
De plus :
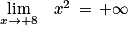
Ainsi par produit :
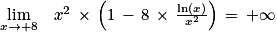
Donc :
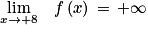
3. Pour tout réel x de ]0 ; 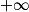 [ :
[ :
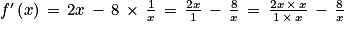
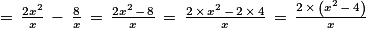
En effet :
La fonction dérivée de la fonction carrée est la fonction linéaire qui, à x, associe 2x.
La fonction dérivée de la fonction logarithme népérien est la fonction inverse.
La fonction dérivée de la somme de deux fonctions est égale à la somme des deux fonctions dérivées des deux fonctions.
On peut écrire tout réel sous la forme de ce réel sur 1.
On a une différence entre deux fractions qui n'ont pas le même dénominateur. Pour pouvoir simplifier l'écriture, il faudrait que les deux fractions possèdent le même dénominateur. Sachant que l'on ne change pas la valeur d'une fraction lorsque l'on multiplie son numérateur et son dénominateur par un même réel, alors on choisit pour la première fraction de multiplier son numérateur et son dénominateur par x. Ainsi, les deux fractions auront maintenant le même dénominateur.
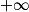 [ :
[ :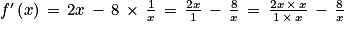
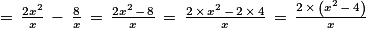
En effet :
| x | 0 | | 2 | | 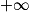 |
| x − 2 | | − | 1 | + | |
| x + 2 | | + | 0 | + | |
| x | 0 | + | 1 | + | |
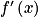 | VI | − | 0 | + | |
La fonction dérivée de la fonction carrée est la fonction linéaire qui, à x, associe 2x.
La fonction dérivée de la fonction logarithme népérien est la fonction inverse.
La fonction dérivée de la somme de deux fonctions est égale à la somme des deux fonctions dérivées des deux fonctions.
On peut écrire tout réel sous la forme de ce réel sur 1.
On a une différence entre deux fractions qui n'ont pas le même dénominateur. Pour pouvoir simplifier l'écriture, il faudrait que les deux fractions possèdent le même dénominateur. Sachant que l'on ne change pas la valeur d'une fraction lorsque l'on multiplie son numérateur et son dénominateur par un même réel, alors on choisit pour la première fraction de multiplier son numérateur et son dénominateur par x. Ainsi, les deux fractions auront maintenant le même dénominateur.
4. Pour étudier les variations de la fonction f, nous allons étudier le signe de 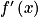 lorsque x appartient à ]0 ;
lorsque x appartient à ]0 ; 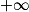 [.
[.
Le dénominateur de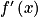 est le réel x. Or x appartient à ]0 ;
est le réel x. Or x appartient à ]0 ; 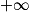 [, donc le dénominateur de
[, donc le dénominateur de 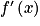 est strictement positif.
est strictement positif.
Le numérateur de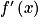 est un polynôme du second degré. Pour pouvoir étudier son signe, deux méthodes sont possibles ici :
est un polynôme du second degré. Pour pouvoir étudier son signe, deux méthodes sont possibles ici :
x2 − 4 = x2 −22 = (x − 2) × (x + 2)
Version LATEX du tableau :
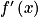 lorsque x appartient à ]0 ;
lorsque x appartient à ]0 ; 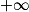 [.
[.Le dénominateur de
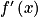 est le réel x. Or x appartient à ]0 ;
est le réel x. Or x appartient à ]0 ; 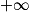 [, donc le dénominateur de
[, donc le dénominateur de 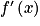 est strictement positif.
est strictement positif.Le numérateur de
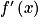 est un polynôme du second degré. Pour pouvoir étudier son signe, deux méthodes sont possibles ici :
est un polynôme du second degré. Pour pouvoir étudier son signe, deux méthodes sont possibles ici : - calcul du discriminant pour trouver les racines du polynôme, puis étude du signe du polynôme grâce au signe du coefficient multipliant x2 ;
- on remarque que l'on peut factoriser facilement le polynôme en un produit de facteurs du type mx + p et on étudie le signe de ces facteurs.
x2 − 4 = x2 −22 = (x − 2) × (x + 2)
Version LATEX du tableau :
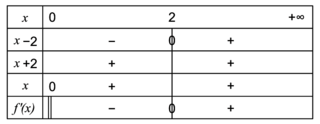 |
En effet :
2 > 0
![x\, \in \, \left ]0\, ;\, +\infty \right [\, \Rightarrow \, x\, > 0 \Rightarrow x + 2 > 0 + 2](https://static1.assistancescolaire.com/t/images/t_spemat_rde29_m36.png)
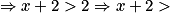
On peut en déduire le tableau de variations de la fonction f.
En effet, pour une fonction f dérivable sur un intervalle I :
2 > 0
![x\, \in \, \left ]0\, ;\, +\infty \right [\, \Rightarrow \, x\, > 0 \Rightarrow x + 2 > 0 + 2](https://static1.assistancescolaire.com/t/images/t_spemat_rde29_m36.png)
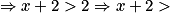
On peut en déduire le tableau de variations de la fonction f.
En effet, pour une fonction f dérivable sur un intervalle I :
• si pour tout x de l'intervalle I 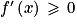 , alors f est croissante sur I
, alors f est croissante sur I
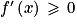 , alors f est croissante sur I
, alors f est croissante sur I• si pour tout x de l'intervalle I 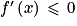 , alors f est décroissante sur I
, alors f est décroissante sur I
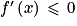 , alors f est décroissante sur I
, alors f est décroissante sur ID'après la dernière ligne du tableau de signes de 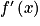 on lit que :
on lit que :
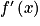 on lit que :
on lit que :• pour tout x de l'intervalle ]0 ; 2] 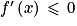 et que pour tout x de l'intervalle [2 ;
et que pour tout x de l'intervalle [2 ;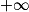 [
[ 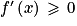 .
.
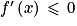 et que pour tout x de l'intervalle [2 ;
et que pour tout x de l'intervalle [2 ;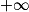 [
[ 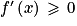 .
.On peut donc en déduire que la fonction f est décroissante sur ]0 ; 2] et croissante sur [2 ; 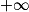 [.
[.
On peut également placer les deux limites étudiées aux questions 1 et 2 dans le tableau de variations.
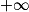 [.
[.On peut également placer les deux limites étudiées aux questions 1 et 2 dans le tableau de variations.
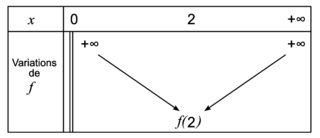 |
Lorsque x = 2, alors 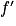 s'annule et change de signe. La fonction f admet donc un minimum atteint lorsque x = 2, il est égal à
s'annule et change de signe. La fonction f admet donc un minimum atteint lorsque x = 2, il est égal à 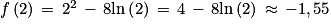 .
.
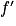 s'annule et change de signe. La fonction f admet donc un minimum atteint lorsque x = 2, il est égal à
s'annule et change de signe. La fonction f admet donc un minimum atteint lorsque x = 2, il est égal à 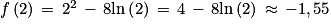 .
.5. La fonction f est strictement décroissante sur ]0 ; 2] car  strictement négative sur ]0 ; 2] (sauf lorsque x = 2 où
strictement négative sur ]0 ; 2] (sauf lorsque x = 2 où  s'annule).
s'annule).
La fonction f est continue sur ]0 ; 2] car elle est dérivable sur ]0 ; 2].
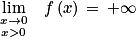
f(2) < 0
Le réel 0 appartient à l'intervalle ]f(2) ; [.
[.
Donc d'après un corollaire du théorème des valeurs intermédiaires : l'équation f(x) = 0 admet une unique solution α appartenant à ]0 ; 2].
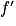 strictement négative sur ]0 ; 2] (sauf lorsque x = 2 où
strictement négative sur ]0 ; 2] (sauf lorsque x = 2 où  s'annule).
s'annule).La fonction f est continue sur ]0 ; 2] car elle est dérivable sur ]0 ; 2].
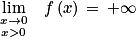
f(2) < 0
Le réel 0 appartient à l'intervalle ]f(2) ;
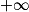 [.
[.Donc d'après un corollaire du théorème des valeurs intermédiaires : l'équation f(x) = 0 admet une unique solution α appartenant à ]0 ; 2].
6. Avec toutes les informations, on peut affirmer que :
• La fonction f est strictement positive sur ]0 ; α[.
• La fonction f s'annule lorsque x = α.
• La fonction f est strictement négative sur ]α ; β[.
• La fonction f s'annule lorsque x = β.
• La fonction f est strictement positive sur ]β ; 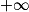 ].
].
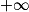 ].
].7. Pour tout réel k, la fonction gk est dérivable sur ]0 ; 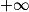 [ en tant que somme de fonctions dérivables sur ]0 ;
[ en tant que somme de fonctions dérivables sur ]0 ; 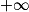 [.
[.
Pour tout réel x de ]0 ;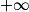 [,
[, 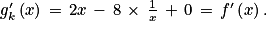
Donc gk et f ont le même sens de variation.
Donc gk admet un minimum atteint lorsque x = 2 qui est égal à :
gk(2) = 22 − 8ln(2) + k
« gk positive sur ]0 ;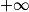 [ est équivalent à « le minimum de gk est positif ».
[ est équivalent à « le minimum de gk est positif ».
On nous demande de chercher la plus petite valeur réelle de k tel que :
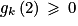
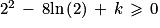
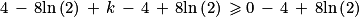
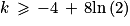
Cette valeur est donc le nombre réel 8ln(2) − 4.
 [ en tant que somme de fonctions dérivables sur ]0 ;
[ en tant que somme de fonctions dérivables sur ]0 ;  [.
[.Pour tout réel x de ]0 ;
 [,
[, 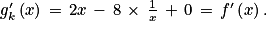
Donc gk et f ont le même sens de variation.
Donc gk admet un minimum atteint lorsque x = 2 qui est égal à :
gk(2) = 22 − 8ln(2) + k
« gk positive sur ]0 ;
 [ est équivalent à « le minimum de gk est positif ».
[ est équivalent à « le minimum de gk est positif ».On nous demande de chercher la plus petite valeur réelle de k tel que :
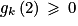
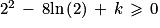
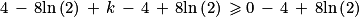
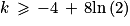
Cette valeur est donc le nombre réel 8ln(2) − 4.

