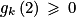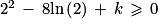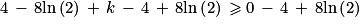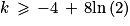Sujet de métropole, mars 2023, exercice 2
Énoncé
Exercice sur 5 points
On considère la fonction f définie sur ]0 ; 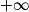 [ par f(x) = x2 − 8 ln(x), où ln désigne la fonction logarithme népérien.
[ par f(x) = x2 − 8 ln(x), où ln désigne la fonction logarithme népérien.
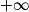 [ par f(x) = x2 − 8 ln(x), où ln désigne la fonction logarithme népérien.
[ par f(x) = x2 − 8 ln(x), où ln désigne la fonction logarithme népérien.On admet que f est dérivable sur ]0 ; 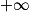 [, on note
[, on note 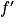 sa fonction dérivée.
sa fonction dérivée.
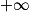 [, on note
[, on note 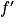 sa fonction dérivée.
sa fonction dérivée.1. Déterminer limx→0 f(x).
2. On admet que, pour tout x > 0, f(x) = x2(1 − 8 ln(x)x2).
En déduire la limite : limx→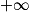 f(x).
f(x).
En déduire la limite : limx→
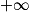 f(x).
f(x).3. Montrer que, pour tout réel x de ]0 ; 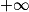 [,
[, 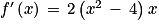 .
.
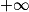 [,
[, 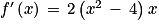 .
.4. Étudier les variations de f sur ]0 ; 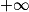 [ et dresser son tableau de variations complet.
[ et dresser son tableau de variations complet.
On précisera la valeur exacte du minimum de f sur ]0 ;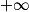 [.
[.
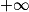 [ et dresser son tableau de variations complet.
[ et dresser son tableau de variations complet.On précisera la valeur exacte du minimum de f sur ]0 ;
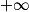 [.
[.5. Démontrer que, sur l'intervalle ]0 ; 2], l'équation f(x) = 0 admet une solution unique α (on ne cherchera pas à déterminer la valeur de α).
6. On admet que, sur l'intervalle [2 ; 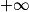 [, l'équation f(x) = 0 admet une solution unique β (on ne cherchera pas à déterminer la valeur de β).
[, l'équation f(x) = 0 admet une solution unique β (on ne cherchera pas à déterminer la valeur de β).
En déduire le signe de f sur l'intervalle ]0 ;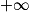 [.
[.
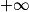 [, l'équation f(x) = 0 admet une solution unique β (on ne cherchera pas à déterminer la valeur de β).
[, l'équation f(x) = 0 admet une solution unique β (on ne cherchera pas à déterminer la valeur de β).En déduire le signe de f sur l'intervalle ]0 ;
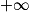 [.
[.7. Pour tout nombre réel k, on considère la fonction gk définie sur ]0 ; 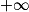 [ par :gk(x) = x2 − 8ln(x) + k
[ par :gk(x) = x2 − 8ln(x) + k
En s'aidant du tableau de variations de f, déterminer la plus petite valeur de k pour laquelle la fonction gk est positive sur l'intervalle ]0 ;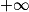 [.
[.
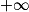 [ par :gk(x) = x2 − 8ln(x) + k
[ par :gk(x) = x2 − 8ln(x) + kEn s'aidant du tableau de variations de f, déterminer la plus petite valeur de k pour laquelle la fonction gk est positive sur l'intervalle ]0 ;
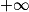 [.
[.Annexes
© 2000-2026, Miscellane
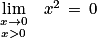
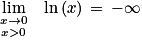
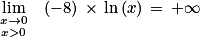
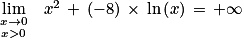
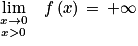
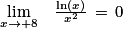
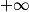 ).
).
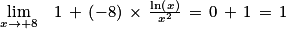
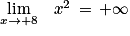
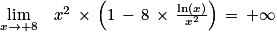
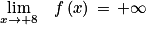
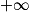 [ :
[ :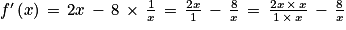
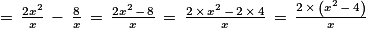
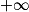
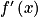
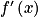 lorsque x appartient à ]0 ;
lorsque x appartient à ]0 ; 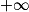 [.
[.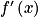 est le réel x. Or x appartient à ]0 ;
est le réel x. Or x appartient à ]0 ;  [, donc le dénominateur de
[, donc le dénominateur de  est strictement positif.
est strictement positif. est un polynôme du second degré. Pour pouvoir étudier son signe, deux méthodes sont possibles ici :
est un polynôme du second degré. Pour pouvoir étudier son signe, deux méthodes sont possibles ici : 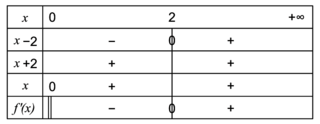
![x\, \in \, \left ]0\, ;\, +\infty \right [\, \Rightarrow \, x\, > 0 \Rightarrow x + 2 > 0 + 2](https://static1.assistancescolaire.com/t/images/t_spemat_rde29_m36.png)
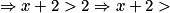
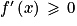 , alors f est croissante sur I
, alors f est croissante sur I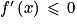 , alors f est décroissante sur I
, alors f est décroissante sur I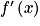 on lit que :
on lit que :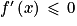 et que pour tout x de l'intervalle [2 ;
et que pour tout x de l'intervalle [2 ;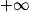 [
[ 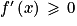 .
.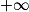 [.
[.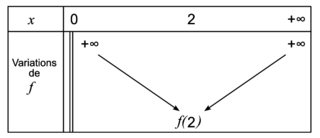
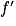 s'annule et change de signe. La fonction f admet donc un minimum atteint lorsque x = 2, il est égal à
s'annule et change de signe. La fonction f admet donc un minimum atteint lorsque x = 2, il est égal à 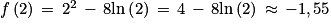 .
.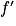 strictement négative sur ]0 ; 2] (sauf lorsque x = 2 où
strictement négative sur ]0 ; 2] (sauf lorsque x = 2 où 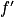 s'annule).
s'annule).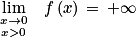
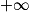 [.
[.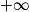 ].
]. [ en tant que somme de fonctions dérivables sur ]0 ;
[ en tant que somme de fonctions dérivables sur ]0 ;  [.
[. [,
[, 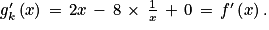
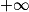 [ est équivalent à « le minimum de gk est positif ».
[ est équivalent à « le minimum de gk est positif ».