Énoncé
Partie 1. Application directe
Le nombre de pièces sortant d'une usine en une journée est une variable aléatoire d'espérance m = 50 et de variance σ2 = 25. On veut estimer la probabilité que la production, un jour donné, dépasse 75 pièces.Partie 2. Intervalle de confiance obtenu avec l'inégalité de Bienaymé-Tchebychev.
Un institut de sondages décide de mener une enquête concernant une élection pour laquelle deux candidats A et B se présentent. On suppose, pour simplifier les choses, que chaque individu sondé répond A ou B, à l'exclusion de toute autre réponse, et que le collège électoral est suffisamment grand pour que les réponses soient considérées comme mutuellement indépendantes. La taille de l'échantillon choisi pour faire le sondage est 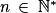 et, pour chaque individu i de l'échantillon, on appelle Xi la variable aléatoire égale à 1 si la réponse est favorable à A, et 0 sinon. Chaque variable Xi est une variable de Bernoulli de paramètre p inconnu que le sondage souhaite bien sûr estimer. Les variables sont indépendantes. On pose
et, pour chaque individu i de l'échantillon, on appelle Xi la variable aléatoire égale à 1 si la réponse est favorable à A, et 0 sinon. Chaque variable Xi est une variable de Bernoulli de paramètre p inconnu que le sondage souhaite bien sûr estimer. Les variables sont indépendantes. On pose 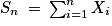 et
et 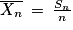 .
.
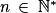 et, pour chaque individu i de l'échantillon, on appelle Xi la variable aléatoire égale à 1 si la réponse est favorable à A, et 0 sinon. Chaque variable Xi est une variable de Bernoulli de paramètre p inconnu que le sondage souhaite bien sûr estimer. Les variables sont indépendantes. On pose
et, pour chaque individu i de l'échantillon, on appelle Xi la variable aléatoire égale à 1 si la réponse est favorable à A, et 0 sinon. Chaque variable Xi est une variable de Bernoulli de paramètre p inconnu que le sondage souhaite bien sûr estimer. Les variables sont indépendantes. On pose 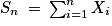 et
et 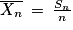 .
.1. Quelle est la loi suivie par Sn ? Que représente 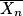 ? Calculer
? Calculer 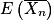 et
et 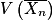 .
.
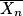 ? Calculer
? Calculer 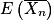 et
et 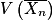 .
.2. Montrer que quel que soit ![x\: \in\: ]0\, ;\, 1[](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m7.png) ,
, 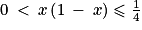 .
.
![x\: \in\: ]0\, ;\, 1[](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m7.png) ,
, 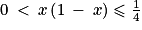 .
.3. Déduire de l'inégalité de Bienaymé-Tchebychev que quel que soit t > 0, ![P\left ( p\: \in \: \left [ \overline{X_{n}}-t\: ; \overline{X_{n}}\: +\: t\right ] \right )\geqslant 1-\frac{1}{4nt^{2}}](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m9.png) .
.
![P\left ( p\: \in \: \left [ \overline{X_{n}}-t\: ; \overline{X_{n}}\: +\: t\right ] \right )\geqslant 1-\frac{1}{4nt^{2}}](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m9.png) .
.4.
Soit 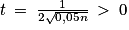 , on a donc :
, on a donc :
![P\left ( p\: \in \left [ \overline{X_{n}}\: -\: \frac{1}{2\sqrt{0,05n}}\: ;\: \overline{X_{n}}\: +\: \frac{1}{2\sqrt{0,05n}}\right ] \right )\geqslant 0,95](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m11.png) .
.
On dit que![\left [ \overline{X_{n}}\: -\: \frac{1}{2\sqrt{0,05n}}\: ;\: \overline{X_{n}}\: +\: \frac{1}{2\sqrt{0,05n}}\right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m12.png) est un intervalle de confiance au niveau de confiance 95 %. Un intervalle de confiance est donc un intervalle aléatoire. Dès que la variable aléatoire
est un intervalle de confiance au niveau de confiance 95 %. Un intervalle de confiance est donc un intervalle aléatoire. Dès que la variable aléatoire 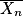 est réalisée et donne la valeur f, l'intervalle
est réalisée et donne la valeur f, l'intervalle ![\left [ f\: -\: \frac{1}{2\sqrt{0,05n}}\: ;\: f\: +\: \frac{1}{2\sqrt{0,05n}}\right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m14.png) qui n'est plus aléatoire est appelé une estimation de p par un intervalle de confiance au niveau de confiance 95 %.
qui n'est plus aléatoire est appelé une estimation de p par un intervalle de confiance au niveau de confiance 95 %.
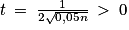 , on a donc :
, on a donc :![P\left ( p\: \in \left [ \overline{X_{n}}\: -\: \frac{1}{2\sqrt{0,05n}}\: ;\: \overline{X_{n}}\: +\: \frac{1}{2\sqrt{0,05n}}\right ] \right )\geqslant 0,95](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m11.png) .
.On dit que
![\left [ \overline{X_{n}}\: -\: \frac{1}{2\sqrt{0,05n}}\: ;\: \overline{X_{n}}\: +\: \frac{1}{2\sqrt{0,05n}}\right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m12.png) est un intervalle de confiance au niveau de confiance 95 %. Un intervalle de confiance est donc un intervalle aléatoire. Dès que la variable aléatoire
est un intervalle de confiance au niveau de confiance 95 %. Un intervalle de confiance est donc un intervalle aléatoire. Dès que la variable aléatoire 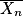 est réalisée et donne la valeur f, l'intervalle
est réalisée et donne la valeur f, l'intervalle ![\left [ f\: -\: \frac{1}{2\sqrt{0,05n}}\: ;\: f\: +\: \frac{1}{2\sqrt{0,05n}}\right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m14.png) qui n'est plus aléatoire est appelé une estimation de p par un intervalle de confiance au niveau de confiance 95 %.
qui n'est plus aléatoire est appelé une estimation de p par un intervalle de confiance au niveau de confiance 95 %.a. On suppose que n = 1000 et que les questionnaires indiquent que 520 personnes sont favorables à A. Donner une estimation de p par un intervalle de confiance au niveau de confiance 95 %.
b. Combien faut-il choisir de sondés pour que p soit estimé par un intervalle de confiance au niveau de confiance 95 % d'amplitude inférieure à 1 % ?
La bonne méthode
Partie 1
On applique l'inégalité de Bienaymé-Tchebychev.Partie 2
1. La variable Sn est la somme de variables de Bernoulli indépendantes et de même paramètre. On utilise les propriétés de l'espérance et de la variance.
2. Une simple étude de fonction permet de conclure.
3. On écrit l'inégalité demandée et on utilise ce qui précède.
4.
a. Il s'agit d'une simple application numérique.
b. Il s'agit d'une simple inéquation à résoudre.
Corrigé
Partie 1
L'inégalité de Bienaymé-Tchebychev dit que si X suit une loi d'espérance m et de variance σ, alors quel que soit x > 0, on a 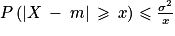 . Ici, il s'agit d'une application directe de la formule :
. Ici, il s'agit d'une application directe de la formule : 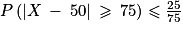 , soit
, soit 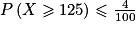 puisque X est à l'évidence une variable aléatoire qui prend ses valeurs dans
puisque X est à l'évidence une variable aléatoire qui prend ses valeurs dans 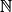 .
.
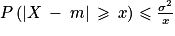 . Ici, il s'agit d'une application directe de la formule :
. Ici, il s'agit d'une application directe de la formule : 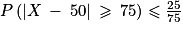 , soit
, soit 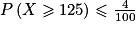 puisque X est à l'évidence une variable aléatoire qui prend ses valeurs dans
puisque X est à l'évidence une variable aléatoire qui prend ses valeurs dans 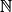 .
.Partie 2
1. Sn est la somme de n variables de Bernoulli indépendantes et de même paramètre p. On sait donc que Sn suit la loi binomiale de paramètres n et p. La variableSn compte le nombre de réponses favorables à A au cours du sondage. Ainsi, 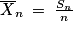 est la moyenne des réponses favorables à A au cours du sondage. On sait que E(Sn) = np et V(Sn) = np(1 − p). Ainsi,
est la moyenne des réponses favorables à A au cours du sondage. On sait que E(Sn) = np et V(Sn) = np(1 − p). Ainsi, 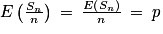 et
et 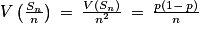 .
.
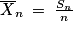 est la moyenne des réponses favorables à A au cours du sondage. On sait que E(Sn) = np et V(Sn) = np(1 − p). Ainsi,
est la moyenne des réponses favorables à A au cours du sondage. On sait que E(Sn) = np et V(Sn) = np(1 − p). Ainsi, 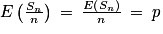 et
et 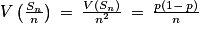 .
.2. C'est clair, la fonction 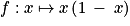 est un polynôme du second degré, de coefficient dominant a = −1 < 0. Elle est donc croissante sur
est un polynôme du second degré, de coefficient dominant a = −1 < 0. Elle est donc croissante sur ![]-\infty ;\frac{1}{2}]](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m23.png) et décroissante sur
et décroissante sur 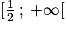 . Par ailleurs, les racines du polynômes sont 0 et 1, et le signe de f(x) est l'opposé de celui de a = −1 à l'intérieur des racines. On en déduit que quel que soit
. Par ailleurs, les racines du polynômes sont 0 et 1, et le signe de f(x) est l'opposé de celui de a = −1 à l'intérieur des racines. On en déduit que quel que soit ![x\: \in \: ]0\: ;\: 1[](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m25.png) ,
, 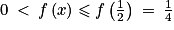 .
.
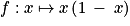 est un polynôme du second degré, de coefficient dominant a = −1 < 0. Elle est donc croissante sur
est un polynôme du second degré, de coefficient dominant a = −1 < 0. Elle est donc croissante sur ![]-\infty ;\frac{1}{2}]](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m23.png) et décroissante sur
et décroissante sur 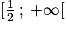 . Par ailleurs, les racines du polynômes sont 0 et 1, et le signe de f(x) est l'opposé de celui de a = −1 à l'intérieur des racines. On en déduit que quel que soit
. Par ailleurs, les racines du polynômes sont 0 et 1, et le signe de f(x) est l'opposé de celui de a = −1 à l'intérieur des racines. On en déduit que quel que soit ![x\: \in \: ]0\: ;\: 1[](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m25.png) ,
, 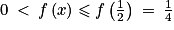 .
.3.
D'après l'inégalité de Bienaymé-Tchebychev, pour tout 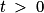 , on a
, on a 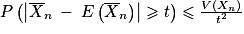 , soit
, soit 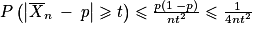 . Donc, en passant à l'événement contraire, on a
. Donc, en passant à l'événement contraire, on a 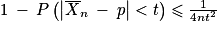 , autrement dit
, autrement dit 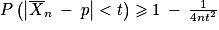 , soit enfin quel que soit t > 0 :
, soit enfin quel que soit t > 0 :
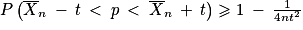 .
.
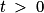 , on a
, on a 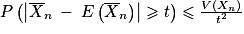 , soit
, soit 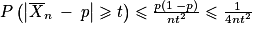 . Donc, en passant à l'événement contraire, on a
. Donc, en passant à l'événement contraire, on a 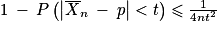 , autrement dit
, autrement dit 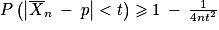 , soit enfin quel que soit t > 0 :
, soit enfin quel que soit t > 0 :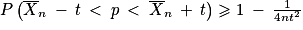 .
.a. La variable 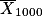 est réalisée en
est réalisée en 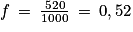 . L'estimation de p par l'intervalle de confiance est donc [0,449 ; 0,591].
. L'estimation de p par l'intervalle de confiance est donc [0,449 ; 0,591].
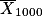 est réalisée en
est réalisée en 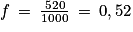 . L'estimation de p par l'intervalle de confiance est donc [0,449 ; 0,591].
. L'estimation de p par l'intervalle de confiance est donc [0,449 ; 0,591].b. L'amplitude de l'intervalle ![\left [ f\: -\: \frac{1}{2\sqrt{0,05n}}\: ; f\: +\: \frac{1}{2\sqrt{0,05n}} \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m35.png) est
est 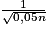 . Il suffit donc que
. Il suffit donc que 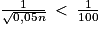 , ce qui conduit à n > 200 000. Il est évident que le nombre de sondés à recruter est trop élevé pour être économiquement viable pour l'entreprise.
, ce qui conduit à n > 200 000. Il est évident que le nombre de sondés à recruter est trop élevé pour être économiquement viable pour l'entreprise.
![\left [ f\: -\: \frac{1}{2\sqrt{0,05n}}\: ; f\: +\: \frac{1}{2\sqrt{0,05n}} \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde18_m35.png) est
est 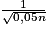 . Il suffit donc que
. Il suffit donc que 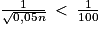 , ce qui conduit à n > 200 000. Il est évident que le nombre de sondés à recruter est trop élevé pour être économiquement viable pour l'entreprise.
, ce qui conduit à n > 200 000. Il est évident que le nombre de sondés à recruter est trop élevé pour être économiquement viable pour l'entreprise.
