Énoncé
Exercice 1 (commun à tous les candidats)
Dans une école de statistique, après étude des dossiers des candidats, le recrutement se fait de deux façons : 10 % des candidats sont sélectionnés sur dossier. Ces candidats doivent ensuite passer un oral, à l'issue duquel 60 % d'entre eux sont finalement admis à l'école ; les candidats n'ayant pas été sélectionnés sur dossier passent une épreuve écrite, à l'issue de laquelle 20 % d'entre eux sont admis à l'école.
Partie 1
On choisit au hasard un candidat à ce concours de recrutement. On notera : D l'événement « le candidat a été sélectionné sur dossier » ; A l'événement, « le candidat a été admis à l'école » ; et les événements contraires des événements D et A, respectivement.
1. Traduire la situation par un arbre pondéré.
Un arbre pondéré est un arbre où l'on met sur les branches des probabilités soit sous forme fractionnaire soit sous forme décimale, mais pas de pourcentages.
2. Calculer la probabilité que le candidat soit sélectionné sur dossier et admis à l'école.
On remarque le « et » dans la probabilité, donc on demande ici la probabilité d'une intersection : on utilise la formule de première 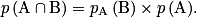
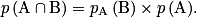
3. Montrer que la probabilité de l'événement A est égale à 0,24.
On cherche ici cela correspond à la formule des probabilités totales vue en première.
4. On choisit au hasard un candidat admis à l'école. Quelle est la probabilité que son dossier n'ait pas été sélectionné ?
Cette question demande une probabilité conditionnelle. Il existe trois cas où l'on doit chercher une probabilité conditionnelle : lorsque, comme ici, on a une phrase et « un point final » : cela signifie que l'ensemble de référence change (ici, on est parmi les candidats admis à l'école, donc parmi les A) ; lorsque le texte contient le mot « parmi » ; lorsque le texte contient les mots « sachant que ». On applique alors la formule du cours : 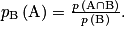
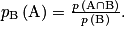
Partie 2
1. On admet que la probabilité pour un candidat d'être admis à l'école est égale à 0,24. On considère un échantillon de sept candidats choisis au hasard, en assimilant ce choix à un tirage au sort avec remise. On désigne par X la variable aléatoire dénombrant les candidats admis à l'école parmi les sept tirés au sort.
a. On admet que la variable aléatoire X suit une loi binomiale. Quels sont les paramètres de cette loi ?
Si la consigne avait demandé de démontrer que l'on a une loi binomiale (ici on l'admet, donc la rédaction est inutile), il aurait fallu rédiger ainsi : On répète 7 fois, de façon identique et indépendante, une expérience à 2 issues : le succès « le candidat est admis à l'école », avec une probabilité p = 0,24 ; et l'échec, son événement contraire. Soit X la variable aléatoire associée au nombre de succès. X suit une loi binomiale de paramètres n = 7 et p = 0,24.
b. Calculer la probabilité qu'un seul des sept candidats tirés au sort soit admis à l'école. On donnera une réponse arrondie au centième.
c. Calculer la probabilité qu'au moins deux des sept candidats tirés au sort soient admis à cette école. On donnera une réponse arrondie au centième.
2. Un lycée présente n candidats au recrutement dans cette école, où n est un entier naturel non nul. On admet que la probabilité pour un candidat quelconque du lycée d'être admis à l'école est égale à 0,24 et que les résultats des candidats sont indépendants les uns des autres.
a. Donner l'expression, en fonction de n, de la probabilité qu'aucun candidat issu de ce lycée ne soit admis à l'école.
C'est encore une loi binomiale. Mais cette fois-ci, nous ne connaissons pas n (en revanche, p est encore égal à 0,24). Donc on donnera les résultats en fonction de n en utilisant la formule du cours.
b. À partir de quelle valeur de l'entier n la probabilité qu'au moins un élève de ce lycée soit admis à l'école est-elle supérieure ou égale à 0,99 ?
Corrigé
Partie I
1. On traduit la situation par un arbre pondéré :
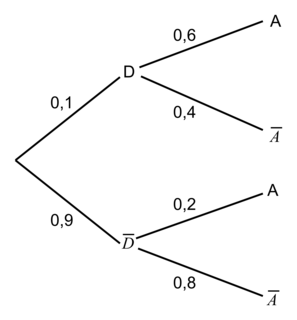 |
2. On choisit un candidat « au hasard », il y a donc équiprobabilité. La probabilité que le candidat soit sélectionné sur dossier et admis à l'école correspond à :
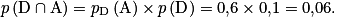
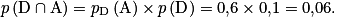
3. 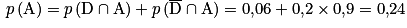 .
.
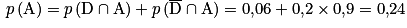 .
. 4. 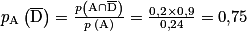 .
.
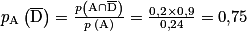 .
. Partie II
1. a. X suit une loi binomiale de paramètres (7 ; 0,24).
b.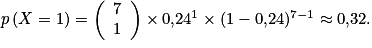
c.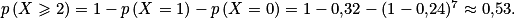
b.
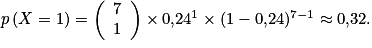
c.
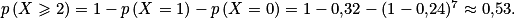
2. a.On cherche 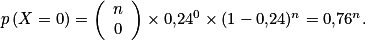
b.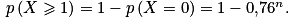
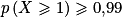 si et seulement si
si et seulement si
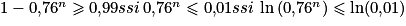
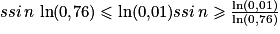
Il faut donc avoir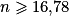 . Donc c'est à partir de 17 élèves que la probabilité qu'au moins un élève de ce lycée soit admis à l'école est supérieure ou égale à 0,99.
. Donc c'est à partir de 17 élèves que la probabilité qu'au moins un élève de ce lycée soit admis à l'école est supérieure ou égale à 0,99.
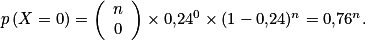
b.
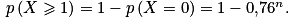
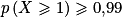 si et seulement si
si et seulement si 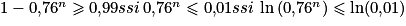
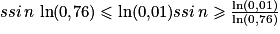
Il faut donc avoir
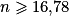 . Donc c'est à partir de 17 élèves que la probabilité qu'au moins un élève de ce lycée soit admis à l'école est supérieure ou égale à 0,99.
. Donc c'est à partir de 17 élèves que la probabilité qu'au moins un élève de ce lycée soit admis à l'école est supérieure ou égale à 0,99.
