Succession d'épreuves indépendantes, schéma de Bernoulli. D'après sujet Bac S, Polynésie, septembre 2010
Énoncé
Un jeu consiste à tirer simultanément 4 boules indiscernables au toucher d'un sac contenant 1 boule noire et 9 boules blanches, puis à lancer un dé bien équilibré à six faces numérotées de 1 à 6.
Si la boule noire est tirée, il faut obtenir un nombre pair avec le dé pour gagner. Si la boule noire n'est pas tirée, il faut obtenir un six avec le dé pour gagner.
On appelle N l'événement : « La boule noire figure parmi les boules tirées », et G l'événement : « Le joueur gagne ».
Si la boule noire est tirée, il faut obtenir un nombre pair avec le dé pour gagner. Si la boule noire n'est pas tirée, il faut obtenir un six avec le dé pour gagner.
On appelle N l'événement : « La boule noire figure parmi les boules tirées », et G l'événement : « Le joueur gagne ».
1.
a. Déterminer la probabilité de l'événement N.
b. Démontrer que la probabilité de l'événement G est égale à 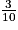 . On pourra s'aider d'un arbre pondéré.
. On pourra s'aider d'un arbre pondéré.
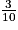 . On pourra s'aider d'un arbre pondéré.
. On pourra s'aider d'un arbre pondéré.c. Le joueur ne gagne pas. Quelle est la probabilité qu'il ait tiré la boule noire
2.
Pour jouer à ce jeu, une mise de départ de m euros est demandée, avec m réel strictement positif.
Si le joueur gagne, il reçoit 4 euros.
S'il ne gagne pas mais qu'il a tiré la boule noire, le joueur récupère sa mise.
S'il ne gagne pas et qu'il n'a pas tiré la boule noire, le joueur perd sa mise.
On appelle X la variable aléatoire donnant le gain algébrique du joueur.
Si le joueur gagne, il reçoit 4 euros.
S'il ne gagne pas mais qu'il a tiré la boule noire, le joueur récupère sa mise.
S'il ne gagne pas et qu'il n'a pas tiré la boule noire, le joueur perd sa mise.
On appelle X la variable aléatoire donnant le gain algébrique du joueur.
a. Déterminer la loi de probabilité de X.
b. Exprimer l'espérance mathématique de X en fonction de m.
c. On dit que le jeu est équitable si l'espérance mathématique de X est nulle. Déterminer m pour que le jeu soit équitable.
3.
Soit n un entier naturel non nul.
On joue n fois à ce jeu, sachant qu'après chaque partie, les boules sont remises dans le sac.
Déterminer la valeur minimale de n pour laquelle la probabilité de gagner au moins une fois est supérieure à 0,999.
On joue n fois à ce jeu, sachant qu'après chaque partie, les boules sont remises dans le sac.
Déterminer la valeur minimale de n pour laquelle la probabilité de gagner au moins une fois est supérieure à 0,999.
La bonne méthode
• 1. a. Les 4 boules étant tirées simultanément, l'univers est constitué de sous-ensembles à 4 éléments.
• b. On pense à la formule des probabilités totales.
• c. On utilise la définition des probabilités conditionnelles.
• 2. a. On cherche les valeurs prises par X et on utilise ce qui précède pour obtenir la loi de probabilité de X.
• b. On revient à la définition de l'espérance d'une variable aléatoire dont on connaît la loi de probabilité.
• c. La question ne présente aucune difficulté.
• 3. Il est essentiel de savoir traduire la répétition d'un nombre fini d'épreuves identiques et indépendantes en termes de schéma de Bernoulli et de connaître la loi de Z comptant le nombre de succès au cours de ce schéma. Il faut également penser à utiliser l'événement contraire de « 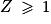 », et savoir utiliser la fonction logarithme népérien.
», et savoir utiliser la fonction logarithme népérien.
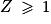 », et savoir utiliser la fonction logarithme népérien.
», et savoir utiliser la fonction logarithme népérien.Corrigé
1.
a. L'énoncé indique clairement qu'on peut supposer l'équiprobabilité des événements élémentaires. Le tirage des 4 boules s'effectue sans remise, l'univers ? est l'ensemble des sous-ensembles à 4 éléments pris parmi 10, ainsi, 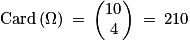 . L'événement N est réalisé lorsque l'on tire la boule noire et 3 boules blanches parmi les 9, ainsi
. L'événement N est réalisé lorsque l'on tire la boule noire et 3 boules blanches parmi les 9, ainsi 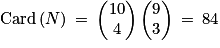 . On a donc
. On a donc 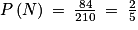 .
.
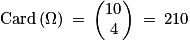 . L'événement N est réalisé lorsque l'on tire la boule noire et 3 boules blanches parmi les 9, ainsi
. L'événement N est réalisé lorsque l'on tire la boule noire et 3 boules blanches parmi les 9, ainsi 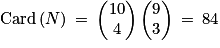 . On a donc
. On a donc 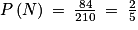 .
.b. On construit un arbre de probabilités :
tikzpicture-1.tex
L'événement G est l'union des événements disjoints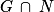 et
et 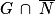 . On a donc
. On a donc 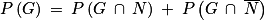 , soit avec la formule des probabilités totales :
, soit avec la formule des probabilités totales : 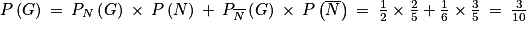 .
.
tikzpicture-1.tex
L'événement G est l'union des événements disjoints
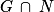 et
et 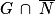 . On a donc
. On a donc 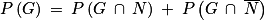 , soit avec la formule des probabilités totales :
, soit avec la formule des probabilités totales : 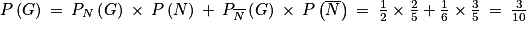 .
.c. L'énoncé demande clairement 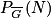 .
. 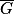 étant un événement de probabilité non nulle, la formule des probabilités composées donne
étant un événement de probabilité non nulle, la formule des probabilités composées donne 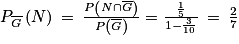 .
.
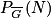 .
. 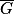 étant un événement de probabilité non nulle, la formule des probabilités composées donne
étant un événement de probabilité non nulle, la formule des probabilités composées donne 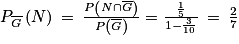 .
.2.
a.
La variable X prend ses valeurs dans X(Ω) = {4 − m, 0, −m}.
• (X = 4 − m) est l'événement « Le joueur a gagné », on a donc 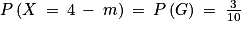 .
.
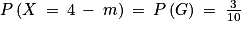 .
.• (X = 0) est l'événement « Le joueur n'a pas gagné mais a tiré la boule noire », on a donc 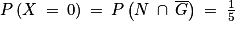 .
.
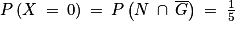 .
.• (X = −m) est l'événement « Le joueur n'a pas gagné et n'a pas tiré la boule noire », on a donc 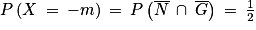 .
.
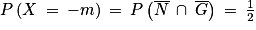 .
.b. E(X) = (4−m)(X = 4 − m) + 0 − P(X = 0) + (−m)P(X = −m).
Ainsi,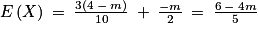 .
.
Ainsi,
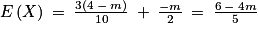 .
.c. 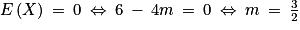 .
.
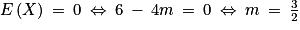 .
.3. Jouer à ce jeu est une épreuve de Bernoulli de paramètre 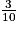 . On joue n fois, les épreuves de Bernoulli sont identiques et indépendantes. La variable aléatoire Z qui compte le nombre de succès au cours de ce schéma de Bernoulli suit la loi binomiale de paramètres n et
. On joue n fois, les épreuves de Bernoulli sont identiques et indépendantes. La variable aléatoire Z qui compte le nombre de succès au cours de ce schéma de Bernoulli suit la loi binomiale de paramètres n et 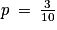 .
.
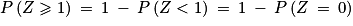 puisque Z(Ω) = [0 ; n]. Ainsi,
puisque Z(Ω) = [0 ; n]. Ainsi, 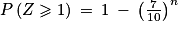 .
.
On a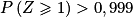 si et seulement si
si et seulement si 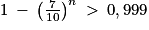 , soit si et seulement si
, soit si et seulement si 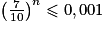 Les quantités en jeu étant strictement positives et la fonction logarithme népérien étant strictement croissante sur
Les quantités en jeu étant strictement positives et la fonction logarithme népérien étant strictement croissante sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde16_m25.png) , l'inéquation est équivalent à n
, l'inéquation est équivalent à n 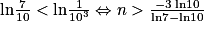 . Le changement de sens de l'inégalité est justifié par le fait que l'on divise par
. Le changement de sens de l'inégalité est justifié par le fait que l'on divise par 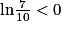 . Le premier entier strictement plus grand que
. Le premier entier strictement plus grand que 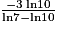 est 20, il faut au moins jouer 20 fois.
est 20, il faut au moins jouer 20 fois.
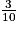 . On joue n fois, les épreuves de Bernoulli sont identiques et indépendantes. La variable aléatoire Z qui compte le nombre de succès au cours de ce schéma de Bernoulli suit la loi binomiale de paramètres n et
. On joue n fois, les épreuves de Bernoulli sont identiques et indépendantes. La variable aléatoire Z qui compte le nombre de succès au cours de ce schéma de Bernoulli suit la loi binomiale de paramètres n et 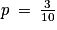 .
.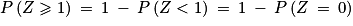 puisque Z(Ω) = [0 ; n]. Ainsi,
puisque Z(Ω) = [0 ; n]. Ainsi, 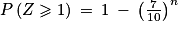 .
.On a
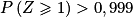 si et seulement si
si et seulement si 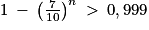 , soit si et seulement si
, soit si et seulement si 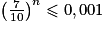 Les quantités en jeu étant strictement positives et la fonction logarithme népérien étant strictement croissante sur
Les quantités en jeu étant strictement positives et la fonction logarithme népérien étant strictement croissante sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde16_m25.png) , l'inéquation est équivalent à n
, l'inéquation est équivalent à n 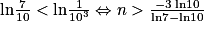 . Le changement de sens de l'inégalité est justifié par le fait que l'on divise par
. Le changement de sens de l'inégalité est justifié par le fait que l'on divise par 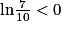 . Le premier entier strictement plus grand que
. Le premier entier strictement plus grand que 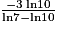 est 20, il faut au moins jouer 20 fois.
est 20, il faut au moins jouer 20 fois.
