Énoncé
Exercice sur 7 points
Le coyote est un animal sauvage proche du loup qui vit en Amérique du Nord.
Dans l'état de l'Oklahoma, aux États-Unis, 70 % des coyotes sont touchés par une maladie appelée ehrlichiose.
Il existe un test aidant à la détection de cette maladie. Lorsque ce test est appliqué à un coyote, son résultat est soit positif, soit négatif, et on sait que :
Dans l'état de l'Oklahoma, aux États-Unis, 70 % des coyotes sont touchés par une maladie appelée ehrlichiose.
Il existe un test aidant à la détection de cette maladie. Lorsque ce test est appliqué à un coyote, son résultat est soit positif, soit négatif, et on sait que :
• Si le coyote est malade, le test est positif dans 97 % des cas.
• Si le coyote n'est pas malade, le test est négatif dans 95 % des cas.
Partie A
Des vétérinaires capturent un coyote de l'Oklahoma au hasard et lui font subir un test pour l'ehrlichiose.
On considère les évènements suivants :
On considère les évènements suivants :
• M : « le coyote est malade » ;
• T : « le test du coyote est positif ».
On note respectivement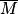 
et 
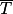les évènements contraires de M et T.
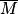et 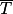les évènements contraires de M et T.1.
Recopier et compléter l'arbre pondéré ci-dessous qui modélise la situation.
 |
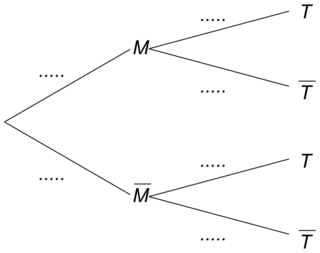Il ne faut pas justifier les réponses, juste faire attention aux valeurs données dans l'énoncé et bien noter les valeurs en écriture décimale sur les branches.
2.
Déterminer la probabilité que le coyote soit malade et que son test soit positif.
On cherche dans cette question la valeur d'une probabilité qui regroupe deux informations. Il faut donc utiliser la formule de la probabilité d'une intersection.
3.
Démontrer que la probabilité de T est égale à 0,694.
On cherche dans cette question la valeur d'une probabilité qui suit deux branches de l'arbre précédent, il faut donc utiliser la formule des probabilités totales.
4.
On appelle « valeur prédictive positive du test » la probabilité que le coyote soit effectivement malade sachant que son test est positif. Calculer la valeur prédictive positive du test. On arrondira le résultat au millième.
On cherche dans cette question la valeur d'une probabilité qui dépend d'une information forcément vraie. Il faut donc utiliser la formule de Bayes donnant la valeur d'une probabilité conditionnelle.
5. a.
Par analogie avec la question précédente, proposer une définition de la « valeur prédictive négative du test » et calculer cette valeur en arrondissant au millième.
Il faut bien lire l'énoncé et comprendre ce que symbolise l'évènement proposé.
On cherche de nouveau dans cette question la valeur d'une probabilité qui dépend d'une information forcément vraie et donc utiliser la formule de Bayes.
On cherche de nouveau dans cette question la valeur d'une probabilité qui dépend d'une information forcément vraie et donc utiliser la formule de Bayes.
5. b. Comparer les valeurs prédictives positive et négative du test puis interpréter.
Il n'y a pas de calculs à faire dans cette question, il faut uniquement comparer les valeurs précédentes et surtout donner une interprétation des résultats obtenus par rapport au problème étudié.
Partie B
On rappelle que la probabilité qu'un coyote capturé au hasard présente un test positif est de 0,694.
1.
Lorsqu'on capture au hasard cinq coyotes, on assimile ce choix à un tirage avec remise. On note X la variable aléatoire qui, à un échantillon de cinq coyotes capturés au hasard, associe le nombre de coyotes dans cet échantillon présentant un test positif.
1. a.
Quelle est la loi de probabilité suivie par X ? Justifier et préciser ses paramètres.
Il y a peu de lois de probabilité à bien connaître. Ici, on reconnaît un schéma qui se répète un certain nombre de fois dans les mêmes conditions, ce qui permet de répondre.
1. b.
Calculer la probabilité que, dans un échantillon de cinq coyotes capturés au hasard, un seul révèle un test positif. On arrondira le résultat au centième.
On utilise les formules du cours et la loi obtenue à la question précédente pour calculer la probabilité cherchée à cette question.
1. c.
Un vétérinaire affirme qu'il y a plus d'une chance sur deux qu'au moins quatre coyotes sur cinq présentent un test positif : cette affirmation est-elle vraie ? Justifier la réponse.
On utilise les formules du cours et la loi obtenue à la question précédente pour calculer la probabilité cherchée à cette question.
Il faut utiliser ici l'évènement contraire à celui qui est cherché pour avoir un calcul plus simple à réaliser.
Il faut utiliser ici l'évènement contraire à celui qui est cherché pour avoir un calcul plus simple à réaliser.
2.
Pour tester des médicaments, les vétérinaires ont besoin de disposer d'un coyote présentant un test positif. Combien doivent-ils capturer de coyotes pour que la probabilité qu'au moins l'un d'entre eux présente un test positif soit supérieure à 0,99 ?
La méthode à utiliser dans cette question est similaire à celle de la question précédente, mais il faut ici résoudre une inéquation. Il faut bien prendre le temps de lire toutes les informations contenues dans la question pour écrire la bonne inéquation au départ.
Corrigé
Partie A
1.
L'arbre pondéré complété est ci-dessous :
 |
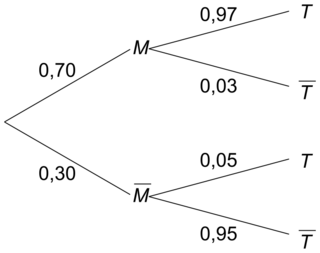2. On calcule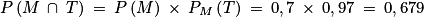 
.
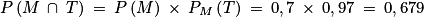.3. D'après la loi des probabilités totales, on a :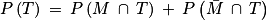 
.
Or, on sait que :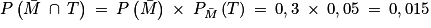
.
Ainsi, on obtient : P(T) = 0,679 + 0,015 = 0,694.
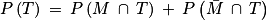.Or, on sait que :
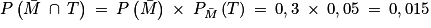.Ainsi, on obtient : P(T) = 0,679 + 0,015 = 0,694.
4. On calcule donc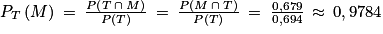 
soit 0,978 si on arrondit la valeur obtenue au millième près.
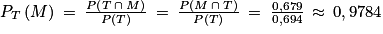soit 0,978 si on arrondit la valeur obtenue au millième près.5. a. On appelle « valeur prédictive négative du test » la probabilité que le coyote ne soit pas malade sachant que son test est négatif.
Elle est égale à :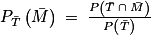
.
Or, on sait que :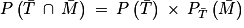
.
De plus, on a :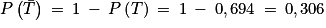
.
Ainsi, on obtient la probabilité cherchée :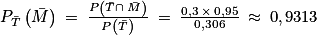
soit 0,931 si on arrondit la valeur au millième près.
Elle est égale à :
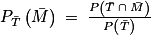.Or, on sait que :
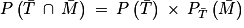.De plus, on a :
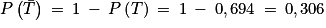.Ainsi, on obtient la probabilité cherchée :
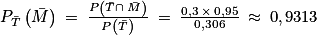soit 0,931 si on arrondit la valeur au millième près.5. b. Comme 0,978 > 0931 cela signifie qu'un résultat probablement positif (erreur d'à peu près 2 %) est plus probant qu'un résultat probablement négatif (erreur d'à peu près 7 %).
Partie B
1.
On note X la variable aléatoire qui, à un échantillon de cinq coyotes capturés au hasard, associe le nombre de coyotes dans cet échantillon présentant un test positif.
1. a. Le nombre de coyotes est assez important pour que toutes les captures indépendantes soient celles d'animaux dont la probabilité de positivité au test est de 0,694. La variable X suit donc une loi binomiale de paramètres n = 5 et p = 0,694.
1. b.
On sait que lorsqu'une variable suit une loi binomiale, on a :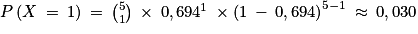 
soit 0,03 si on arrondit la valeur au centième près.
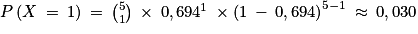soit 0,03 si on arrondit la valeur au centième près.1. c.
Pour répondre à cette affirmation, on vérifie si effectivement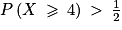 
.
Or, dans cette situation : P(X
4) = P(X = 4) + P(X = 5).
De plus,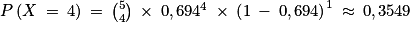
et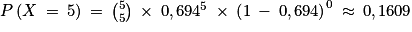 
.
Donc P(X 4) ≈ 0,354 9 + 0,169 9, soit P(X 4) ≈ 0,515 8 qui est une valeur supérieure à 0,5 : le vétérinaire a raison dans son affirmation.
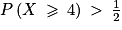.Or, dans cette situation : P(X
4) = P(X = 4) + P(X = 5).De plus,
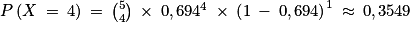et 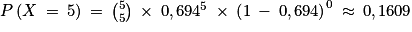.Donc P(X
4) ≈ 0,354 9 + 0,169 9, soit P(X 4) ≈ 0,515 8 qui est une valeur supérieure à 0,5 : le vétérinaire a raison dans son affirmation.2.
Il faut trouver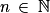 
tel que P(Y 1) > 0,99 avec Y comme variable aléatoire associée au nombre de coyotes ayant un test positif.
On sait que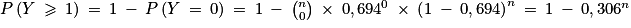
.
Il faut donc résoudre dans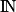
l'inéquation : 
.
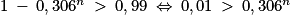Par croissance de la fonction du logarithme népérien, on obtient : ln(001) > ln(0,306n), soit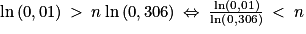
car ln(0,306) < 0.
Comme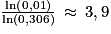
, il faut donc capturer au moins 4 coyotes.
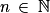tel que P(Y 1) > 0,99 avec Y comme variable aléatoire associée au nombre de coyotes ayant un test positif.On sait que
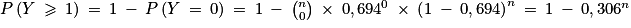.Il faut donc résoudre dans
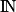l'inéquation : 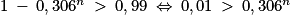.Par croissance de la fonction du logarithme népérien, on obtient : ln(001) > ln(0,306n), soit
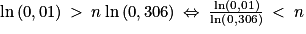car ln(0,306) < 0.Comme
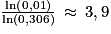, il faut donc capturer au moins 4 coyotes.
