Signaler une erreur
Spécialité mathématiques - Travailler sur des sujets du bac
Manipulation des vecteurs, des droites et des plans de l'espace
Spécialité mathématiques - Travailler sur des sujets du bac
Manipulation des vecteurs, des droites et des plans de l'espace
Imprimer
Spécialité mathématiques - Travailler sur des sujets du bac
Manipulation des vecteurs, des droites et des plans de l'espace
Spécialité mathématiques - Travailler sur des sujets du bac
Manipulation des vecteurs, des droites et des plans de l'espace
Énoncé
ABCDEFGH est un cube.
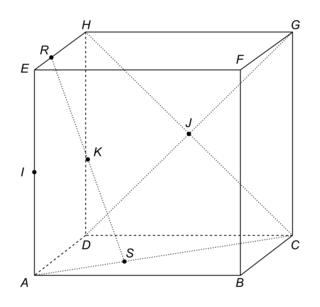 |
On a placé les points I, J, K, R et S tels que :
- I milieu de [AE] ;
- J centre de la face CDHG ;
- R vérifie
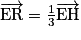 ;
; - S vérifie
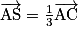 ;
; - K milieu de [RS].
1.a. Justifier que (ABD) est un plan.
b. Exprimer le vecteur 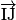 en fonction des vecteurs
en fonction des vecteurs 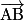 et
et 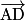
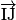 en fonction des vecteurs
en fonction des vecteurs 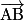 et
et 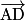
c. En déduire la position relative de la droite (IJ) et du plan (ABD).
2.a. Exprimer le vecteur 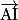 en fonction du vecteur
en fonction du vecteur 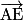 .
.
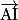 en fonction du vecteur
en fonction du vecteur 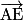 .
.b. Exprimer le vecteur 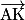 en fonction des vecteurs
en fonction des vecteurs 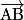 ,
, 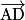 et
et 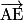 .
.
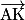 en fonction des vecteurs
en fonction des vecteurs 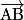 ,
, 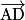 et
et 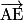 .
.c. En déduire l'expression du vecteur 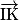 en fonction des vecteurs
en fonction des vecteurs 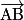 ,
, 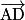 et
et 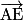 .
.
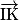 en fonction des vecteurs
en fonction des vecteurs 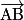 ,
, 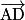 et
et 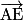 .
.3.a. En utilisant les vecteurs 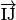 et
et 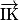 , démonter que les points I, J et K sont alignés.
, démonter que les points I, J et K sont alignés.
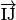 et
et 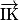 , démonter que les points I, J et K sont alignés.
, démonter que les points I, J et K sont alignés.b. En déduire que les points I, J, K, R et S sont coplanaires.
La bonne méthode
1.a. Utiliser la définition du cours.
b. Utiliser la relation de Chasles en introduisant les points A et D.
c. Utiliser la combinaison linéaire des vecteurs.
2.a. Utiliser que le point I est le milieu du segment [AE].
b. Cette question est plus complexe. Il faut utiliser la relation de Chasles en introduisant les points S, A et E.
c. Regrouper les deux réponses précédentes.
3.a. Utiliser les réponses du 1.b. et du 2.c., et la colinéarité des vecteurs.
b. Il faut commencer par justifier que les droites (IJ) et (RS) sont sécantes en K.
Corrigé
1.a. Les points A, B et D ne sont pas alignés donc (ABD) est un plan de l'espace.
b. 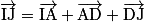
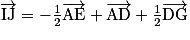
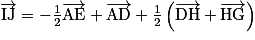
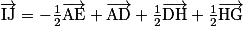
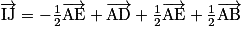
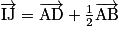
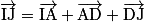
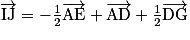
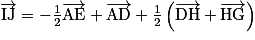
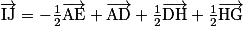
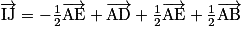
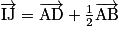
c. 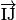 est une combinaison linéaire des vecteurs
est une combinaison linéaire des vecteurs 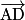 et
et 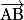 donc la droite (IJ) est parallèle au plan (ABD).
donc la droite (IJ) est parallèle au plan (ABD).
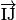 est une combinaison linéaire des vecteurs
est une combinaison linéaire des vecteurs 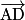 et
et 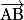 donc la droite (IJ) est parallèle au plan (ABD).
donc la droite (IJ) est parallèle au plan (ABD).2.a. Le point I est le milieu du segment [AE], donc 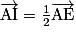 .
.
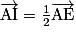 .
.b. 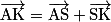
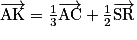
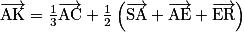
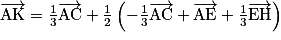
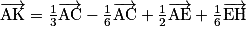
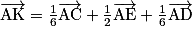
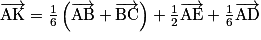
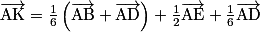
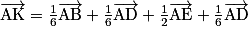
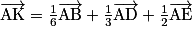
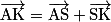
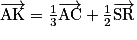
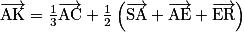
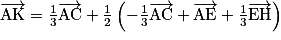
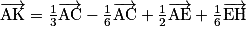
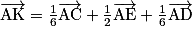
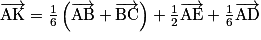
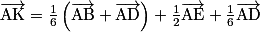
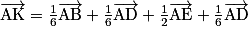
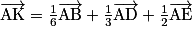
c. 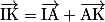
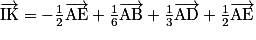
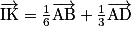
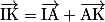
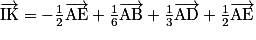
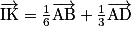
3.a. 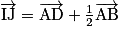 et
et 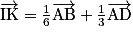 . Donc
. Donc 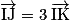
Les vecteurs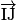 et
et 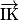 sont colinéaires, donc les points I, J et K sont alignés.
sont colinéaires, donc les points I, J et K sont alignés.
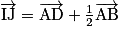 et
et 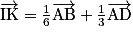 . Donc
. Donc 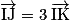
Les vecteurs
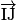 et
et 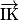 sont colinéaires, donc les points I, J et K sont alignés.
sont colinéaires, donc les points I, J et K sont alignés.b. Le point K appartient aux droites (IJ) et (RS), donc les droites (IJ) et (RS) sont sécantes et forment un plan.
Par conséquent, les points I, J, K, R et S sont coplanaires.
Par conséquent, les points I, J, K, R et S sont coplanaires.
Corrigé
1.a. Les points A, B et D ne sont pas alignés donc (ABD) est un plan de l'espace.
b. 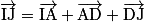
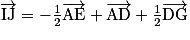
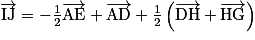
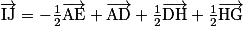
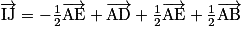
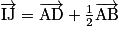
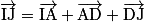
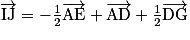
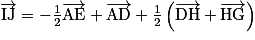
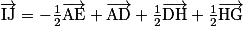
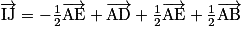
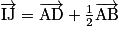
c. 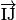 est une combinaison linéaire des vecteurs
est une combinaison linéaire des vecteurs 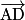 et
et 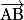 donc la droite (IJ) est parallèle au plan (ABD).
donc la droite (IJ) est parallèle au plan (ABD).
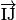 est une combinaison linéaire des vecteurs
est une combinaison linéaire des vecteurs 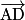 et
et 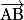 donc la droite (IJ) est parallèle au plan (ABD).
donc la droite (IJ) est parallèle au plan (ABD).2.a. Le point I est le milieu du segment [AE], donc 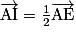 .
.
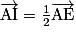 .
.b. 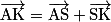
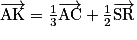
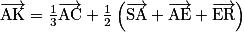
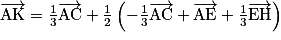
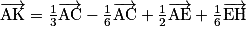
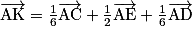
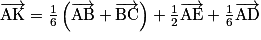
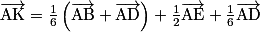
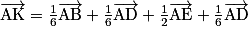
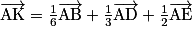
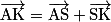
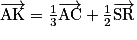
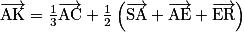
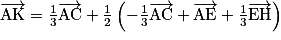
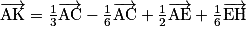
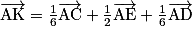
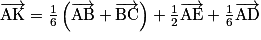
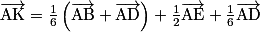
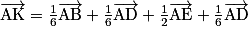
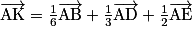
c. 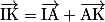
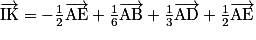
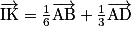
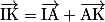
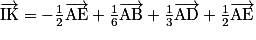
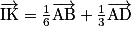
3.a. 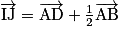 et
et 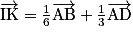 . Donc
. Donc 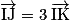
Les vecteurs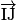 et
et 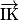 sont colinéaires, donc les points I, J et K sont alignés.
sont colinéaires, donc les points I, J et K sont alignés.
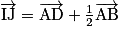 et
et 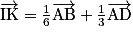 . Donc
. Donc 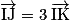
Les vecteurs
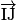 et
et 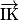 sont colinéaires, donc les points I, J et K sont alignés.
sont colinéaires, donc les points I, J et K sont alignés.b. Le point K appartient aux droites (IJ) et (RS), donc les droites (IJ) et (RS) sont sécantes et forment un plan.
Par conséquent, les points I, J, K, R et S sont coplanaires.
Par conséquent, les points I, J, K, R et S sont coplanaires.
Signaler une erreur
Spécialité mathématiques - Travailler sur des sujets du bac
Manipulation des vecteurs, des droites et des plans de l'espace
Spécialité mathématiques - Travailler sur des sujets du bac
Manipulation des vecteurs, des droites et des plans de l'espace
Imprimer
Spécialité mathématiques - Travailler sur des sujets du bac
Manipulation des vecteurs, des droites et des plans de l'espace
Spécialité mathématiques - Travailler sur des sujets du bac
Manipulation des vecteurs, des droites et des plans de l'espace

