On approfondit dans ce chapitre l'étude de l'espérance et de la variance dans le cadre des variables aléatoires finies. La linéarité de l'espérance donne un outil très puissant permettant de déterminer l'espérance d'une variable aléatoire sans avoir à en déterminer la loi. L'additivité de la variance pour les variables indépendantes est présentée dans le cadre de la succession d'épreuves indépendantes.
I. Comment peut-on calculer la somme de deux variables aléatoires discrètes ?
Soit E une expérience aléatoire et Ω son univers associé. Soient X et Y deux variables aléatoires discrètes, avec X(Ω) = {x1 ; x2 ; … ; xn} et Y (Ω) = {y1 ; y2 ; … ; ym} (n et m deux entiers naturels non nuls). On peut définir la variable aléatoire Z telle que Z = X + Y, avec pour tout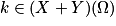 :
: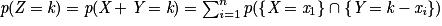
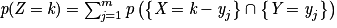
Exemple : On lance un dé à 6 faces (3 faces blanches et 3 faces noires) et un dé à 4 faces (1 face rouge et 3 faces bleues) en même temps. On note Ω l'univers associé à cette expérience aléatoire. Une face blanche rapporte 1 point, une face noire 2 points, une face rouge 3 points et une face bleue 4 points.
On note S la variable aléatoire égale au nombre de points apportés par le dé à 6 faces, et Q la variable aléatoire égale au nombre de points rapportés par le dé à 4 faces. On a donc :
Ω = {(Blanc, Rouge), (Blan, Bleu), (Noir, Rouge), (Noir, Bleu)}
S(Ω) = {1; 2} et Q(Ω) = {3; 4}.
On a :
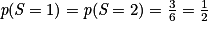 ,
, 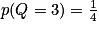 et
et 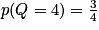 .
.On peut créer une variable aléatoire Z portant sur le nombre de points apportés par les deux dés.
On a Z = S + Q et Z(Ω) = (S + Q)(Ω) = {1 + 3 ; 1 + 4 ; 2 + 3 ; 2+ 4} = {4 ; 5 ; 6}.
Donc
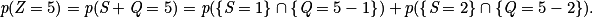
Soit :
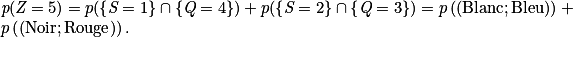
À l'aide d'un arbre pondéré, on trouve facilement :
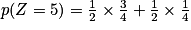 .
.En procédant de la même manière pour les autres valeurs, on obtient la loi de probabilité de Z :
| Zi | 4 | 5 | 6 |
| p(Z = Zi) | 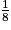 | 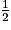 | 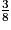 |
II. Que faut-il retenir concernant la linéarité de l'espérance ?
Soit X une variable aléatoire discrète telle que X(Ω) = {x1 ; x2 ; … ; xn}. L'espérance mathématique de X est le nombre réel, noté E(X), qui vérifie :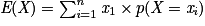 .
.Propriété 1 : Soient X et Y deux variables aléatoires discrètes. On a : E(X + Y) = E(X) + E(Y).
Exemple : Si l'on reprend l'exemple avec les deux dés aux faces colorées, on a
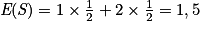 et
et 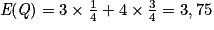 . On a donc E(Z) = E(S + Q) = E(S) + E(Q) = 1,5 + 3,75 = 5,25.
. On a donc E(Z) = E(S + Q) = E(S) + E(Q) = 1,5 + 3,75 = 5,25.On peut aussi vérifier, grâce à la loi de Z, que
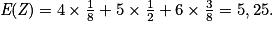
Propriété 2 : Soient a et b deux réels. Soit X une variable aléatoire discrète. On a : E(aX + b) = aE(X) + b.
Exemple : On lance une pièce de monnaie truquée qui vérifie : p(Pile) = 0,7. Pour ce jeu, il n'y a pas de mise de départ ; obtenir pile rapporte 3 euros, obtenir face fait perdre 2 euros.
Soit G la variable aléatoire donnant le gain algébrique du joueur après une partie.
G admet comme loi de probabilité :
| gi | −2 | 3 |
| p(G = gi) | 0,3 | 0,7 |
Alors : E(G) = −2 × 0,3 + 3×0,7 = 1,5.
Les règles du jeu changent : les gains et les pertes sont doublés.
Au lieu de recommencer l'exemple, on peut utiliser une variable aléatoire H telle que H = 2G.
On obtient : E(H) = E(2G) = 2 × E(G) = 2 × 1,5 = 3.
III. Que faut-il retenir sur les variables aléatoires discrètes indépendantes ?
Soit E une expérience aléatoire et Ω son univers associé. Soient X et Y deux variables aléatoires discrètes avec X(Ω) = {x1 ; x2 ; … ; xn} et Y(Ω) = {Y1 ; y2 ; … ; ym} (n et m deux entiers naturels non nuls).
Les variables aléatoires X et Y sont indépendantes si et seulement si pour tout entier i et tout entier j tels que 1 i
i  n et 1
n et 1  j
j  m, on a :
m, on a : 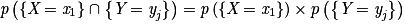 .
.
Soit X une variable aléatoire discrète telle que X(Ω) = {x1 ; x2 ; … ; xn}. La variance de X est le nombre réel, noté V(X), qui vérifie :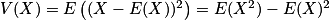 .
.
Propriété 1 : Si X et Y sont deux variables aléatoires discrètes indépendantes, alors V(X + Y) = V(X) + V(Y).
Exemple : Si l'on reprend l'exemple avec les deux dés aux faces colorées, on a :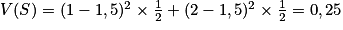 et
et 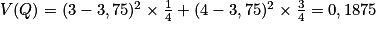 .
.
Alors V(Z) = V(S + Q) = V(S) + V(Q), car S et Q sont indépendantes (les deux dés sont lancés en même temps, et le résultat du premier dé n'a aucune influence sur le résultat du second.
Donc V(Z) = 0,25 + 0,1875 = 0,4375.
Propriété 2 : Soit a un réel et X une variable aléatoire discrète. On a : V(aX) = a2V(X).
Exemple : On lance de nouveau la pièce de monnaie truquée qui vérifie : p(Pile) = 0,7.
La variable aléatoire G donnant le gain algébrique du joueur après une partie n'est pas modifiée.
On avait : E(G) = 1,5.
On a : V(G) = (−2−1,5)2 × 0,3 + (3 − 1,5)2 × 0,7 = 5,25.
Les règles du jeu changent : les gains et les pertes sont triplés. On peut utiliser une variable aléatoire H telle que H = 3G.
On obtient : V(H) = V(3G) = 32 ×V(G) = 9×5,25 = 47,25.
Les variables aléatoires X et Y sont indépendantes si et seulement si pour tout entier i et tout entier j tels que 1
 i
i  n et 1
n et 1  j
j  m, on a :
m, on a : 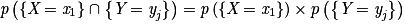 .
.Soit X une variable aléatoire discrète telle que X(Ω) = {x1 ; x2 ; … ; xn}. La variance de X est le nombre réel, noté V(X), qui vérifie :
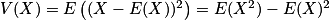 .
.Propriété 1 : Si X et Y sont deux variables aléatoires discrètes indépendantes, alors V(X + Y) = V(X) + V(Y).
Exemple : Si l'on reprend l'exemple avec les deux dés aux faces colorées, on a :
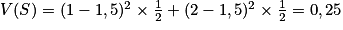 et
et 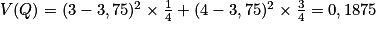 .
.Alors V(Z) = V(S + Q) = V(S) + V(Q), car S et Q sont indépendantes (les deux dés sont lancés en même temps, et le résultat du premier dé n'a aucune influence sur le résultat du second.
Donc V(Z) = 0,25 + 0,1875 = 0,4375.
Propriété 2 : Soit a un réel et X une variable aléatoire discrète. On a : V(aX) = a2V(X).
Exemple : On lance de nouveau la pièce de monnaie truquée qui vérifie : p(Pile) = 0,7.
La variable aléatoire G donnant le gain algébrique du joueur après une partie n'est pas modifiée.
On avait : E(G) = 1,5.
On a : V(G) = (−2−1,5)2 × 0,3 + (3 − 1,5)2 × 0,7 = 5,25.
Les règles du jeu changent : les gains et les pertes sont triplés. On peut utiliser une variable aléatoire H telle que H = 3G.
On obtient : V(H) = V(3G) = 32 ×V(G) = 9×5,25 = 47,25.
IV. Que faut-il retenir sur l'échantillon d'une loi de probabilité
Soit n un entier naturel non nul. Un échantillon de taille n d'une loi de probabilité est une liste (X1, X2, …, Xn) de n variables aléatoires indépendantes identiques suivant cette loi.
Propriétés : Soit (X1, X2, …, Xn) un échantillon d'une loi de probabilité. Soient les deux variables aléatoires Sn et Mn telles que : Sn = X1 + X2 + … + Xn et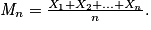
Propriétés : Soit (X1, X2, …, Xn) un échantillon d'une loi de probabilité. Soient les deux variables aléatoires Sn et Mn telles que : Sn = X1 + X2 + … + Xn et
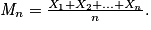
• E(Sn) = n × E(X1) et E(Mn) = E(X1).
• V(Sn) = n×V(X1) et 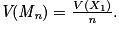
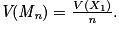
• 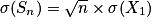 et
et 
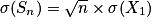 et
et 
V. Que faut-il retenir concernant la loi binomiale ?
Propriétés : Soit (X1, X2, …, Xn) un échantillon de la loi de Bernoulli de paramètre ![p (p\in [0;1])](https://static1.assistancescolaire.com/t/images/t_spemat_14_m25.png) . Alors la variable aléatoire X = X1 + X2 + … Xn suit la loi binomiale de paramètres n et p.
. Alors la variable aléatoire X = X1 + X2 + … Xn suit la loi binomiale de paramètres n et p.
E(X) = np, V(X) = np(1 − p) et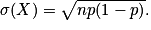
Démonstrations :
Pour tout entier i tel que 1 i
i  n,
n, 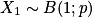 , alors on a : E(Xi) = p ; V(Xi) = p(1 − p) et
, alors on a : E(Xi) = p ; V(Xi) = p(1 − p) et 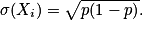
Avec les propriétés de l'espérance et de la variance, on obtient pour la variable aléatoire X : E(X) = n×p, V(X) = n × p(1 − p) et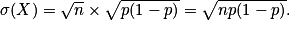
Exemple : Un sac contient trois jetons : un jeton A, un jeton S et un jeton P. Une partie consiste à choisir un jeton au hasard ; on gagne si on tire le jeton A. Kate effectue 10 parties. On peut modéliser la situation à l'aide d'une variable aléatoire X. On a alors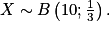
![p (p\in [0;1])](https://static1.assistancescolaire.com/t/images/t_spemat_14_m25.png) . Alors la variable aléatoire X = X1 + X2 + … Xn suit la loi binomiale de paramètres n et p.
. Alors la variable aléatoire X = X1 + X2 + … Xn suit la loi binomiale de paramètres n et p.E(X) = np, V(X) = np(1 − p) et
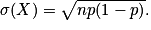
Démonstrations :
Pour tout entier i tel que 1
 i
i  n,
n, 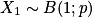 , alors on a : E(Xi) = p ; V(Xi) = p(1 − p) et
, alors on a : E(Xi) = p ; V(Xi) = p(1 − p) et 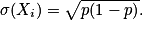
Avec les propriétés de l'espérance et de la variance, on obtient pour la variable aléatoire X : E(X) = n×p, V(X) = n × p(1 − p) et
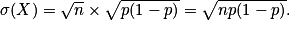
Exemple : Un sac contient trois jetons : un jeton A, un jeton S et un jeton P. Une partie consiste à choisir un jeton au hasard ; on gagne si on tire le jeton A. Kate effectue 10 parties. On peut modéliser la situation à l'aide d'une variable aléatoire X. On a alors
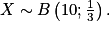
• 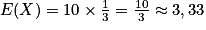 .
.
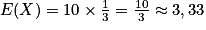 .
.• 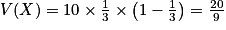 et
et 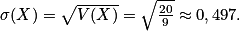
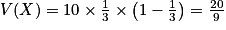 et
et 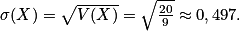
• Cela signifie que si Kate répète un très grand nombre de fois son expérience aléatoire de « jouer à 10 parties », elle gagnera en moyenne environ 3,33 parties par expérience avec une dispersion moyenne de 0,5 partie.
Pour aller plus loin : d'autres lois
Dans ces deux premiers chapitres, nous avons traité l'étude de deux lois discrètes (la loi de Bernoulli et la loi binomiale) et de leurs indicateurs (l'espérance, la variance et l'écart type). Il existe cependant deux autres lois discrètes bien connues et utiles que nous allons aborder ici.
Loi uniforme
Cette loi permet de modéliser des situations d'équiprobabilités, comme le lancer d'un dé équilibré.On dit qu'une variable aléatoire X suit une loi uniforme discrète lorsqu'elle prend ses valeurs dans l'univers Ω = {1 ; … ; n} avec des probabilités qui sont toutes égales pour chaque élément de Ω choisi.
On a alors : pour tout
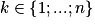 ,
, 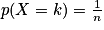 .
.On calcule assez facilement les indicateurs de la loi uniforme :
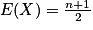 et
et 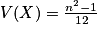 .
.Loi de Poisson
Cette loi permet de modéliser les événements rares, comme le nombre d'appels reçus par un standard téléphonique, ou le nombre de voyageurs se présentant à un guichet dans la journée.On dit qu'une variable aléatoire X suit une loi de Poisson de paramètre λ > 0, notée P(λ), lorsque X(Ω) =
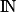 et pour tout
et pour tout 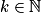 ,
, 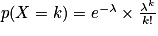 .
.Dans le cas de la loi de Poisson, on a : E(X) = λ et V(X) = λ.
Approximation d'une loi binomiale par une loi de Poisson
On peut parfois réaliser une approximation d'une loi binomiale par une loi de Poisson :Si X suit une loi binomiale de paramètres n et p, avec n grand (n
 30) et p petit (p
30) et p petit (p  0,1), alors pour tout k
0,1), alors pour tout k  0,
0, 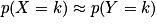 , où Y suit une loi de Poisson de paramètre λ = n × p.
, où Y suit une loi de Poisson de paramètre λ = n × p.
