Les probabilités sont un domaine des mathématiques de plus en plus abordé en classe. Cela commence au collège par l'étude d'événements simples qui font appel à la logique. Au lycée, on diversifie et on approfondit les modèles probabilistes rencontrés, en exploitant des situations où interviennent les probabilités conditionnelles, l'indépendance, les variables aléatoires. L'axe majeur traité dans ce chapitre est l'étude de la succession d'un nombre quelconque d'épreuves aléatoires indépendantes.
I. Que faut-il savoir sur la loi de Bernoulli ?
Ici, p désigne un réel de l'intervalle [0 ; 1]. Une épreuve de Bernoulli de paramètre p est une épreuve à deux issues possibles, nommées succès et échec, telle que la probabilité du succès soit égale à p.
Arbre pondéré représentant une épreuve de Bernoulli :
Arbre pondéré représentant une épreuve de Bernoulli :
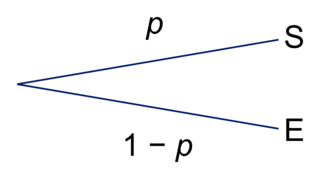 |
On peut noter S l'événement « obtenir le succès », et E l'événement « obtenir l'échec ».
On a donc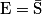 . Comme
. Comme 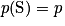 et
et 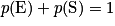 , on a
, on a 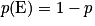 .
.
On peut aussi définir la loi de Bernoulli de paramètre p comme étant la loi de la variable aléatoire qui prend la valeur 1 en cas de succès et 0 en cas d'échec.
Notation : Si X est une variable aléatoire discrète suivant la loi de Bernoulli de paramètre p alors on note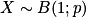 ou parfois
ou parfois 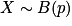 .
.
Tableau représentant la loi de probabilité de X avec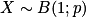 :
:
Exemple : Jeter un dé et considérer que le succès est obtenir un 6. La variable aléatoire X suivant la loi de Bernoulli de paramètre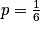 , associée à cette expérience, a pour loi de probabilité :
, associée à cette expérience, a pour loi de probabilité :
Propriétés : Si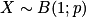 , alors on a trois formules qui donnent la valeur de l'espérance, de la variance et de l'écart type de la variable aléatoire X en fonction du paramètre : p : E(X) = p, V(X) = p(1 − p) et
, alors on a trois formules qui donnent la valeur de l'espérance, de la variance et de l'écart type de la variable aléatoire X en fonction du paramètre : p : E(X) = p, V(X) = p(1 − p) et 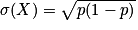 .
.
Exemple : Dans le cas du dé étudié précédemment, on a :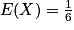 ,
, 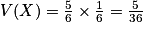 et
et 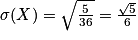 .
.
On a donc
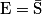 . Comme
. Comme 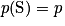 et
et 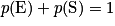 , on a
, on a 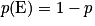 .
.On peut aussi définir la loi de Bernoulli de paramètre p comme étant la loi de la variable aléatoire qui prend la valeur 1 en cas de succès et 0 en cas d'échec.
Notation : Si X est une variable aléatoire discrète suivant la loi de Bernoulli de paramètre p alors on note
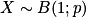 ou parfois
ou parfois 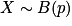 .
.Tableau représentant la loi de probabilité de X avec
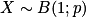 :
: 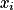 | 0 | 1 |
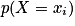 | 1 − p | p |
Exemple : Jeter un dé et considérer que le succès est obtenir un 6. La variable aléatoire X suivant la loi de Bernoulli de paramètre
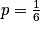 , associée à cette expérience, a pour loi de probabilité :
, associée à cette expérience, a pour loi de probabilité : 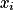 | 0 | 1 |
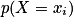 | 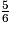 | 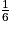 |
Propriétés : Si
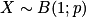 , alors on a trois formules qui donnent la valeur de l'espérance, de la variance et de l'écart type de la variable aléatoire X en fonction du paramètre : p : E(X) = p, V(X) = p(1 − p) et
, alors on a trois formules qui donnent la valeur de l'espérance, de la variance et de l'écart type de la variable aléatoire X en fonction du paramètre : p : E(X) = p, V(X) = p(1 − p) et 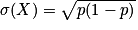 .
.Exemple : Dans le cas du dé étudié précédemment, on a :
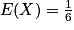 ,
, 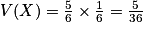 et
et 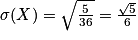 .
.II. Que faut-il savoir sur la loi binomiale ?
Un schéma de Bernoulli de paramètres (n ; p) est la répétition indépendante de n épreuves de Bernoulli identiques, de même paramètre p.Remarque : On peut représenter un schéma de Bernoulli par un arbre pondéré qui comporte n niveaux.
On peut aussi définir la loi binomiale de paramètres n et p comme étant la loi de la variable aléatoire qui compte le nombre de succès dans la répétition de n épreuves de Bernoulli indépendantes de paramètre p.
Notation : Si X est une variable aléatoire discrète suivant la loi binomiale de paramètres n et p, alors on note
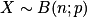 .
.Exemple : Un sac contient trois jetons : un jeton A, un jeton S et un jeton P. Une partie consiste à choisir un jeton au hasard. On gagne la partie si l'on a tiré le jeton A. Kate effectue 10 parties. On aimerait calculer la probabilité qu'elle gagne les 10 parties. On a répété de manière identique et indépendante n = 10 fois l'épreuve de Bernoulli : « Effectuer une partie » dont le succès « Gagner la partie » a pour probabilité
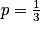 .
.Soit X la variable aléatoire qui compte le nombre de succès.
On a alors
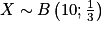 .
.Donc on a : p({X = 10}) =
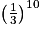 .
.En effet, avec un arbre pondéré représentant la situation, on observe qu'un seul chemin représente une succession de 10 succès, et sur les 10 branches de ce chemin est inscrit le réel
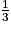 .
.De la même manière, pour n'avoir aucun succès, on a : p({X = 0}) =
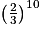 .
.Soit k un entier compris entre 0 et n.
Le nombre
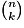 , appelé coefficient binomial, correspond au nombre de chemins qui réalisent exactement k succès dans l'arbre à n niveaux, associé à un schéma de Bernoulli.
, appelé coefficient binomial, correspond au nombre de chemins qui réalisent exactement k succès dans l'arbre à n niveaux, associé à un schéma de Bernoulli.Rappel :
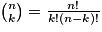
Propriété : soient
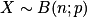 et k un entier compris entre 0 et n.
et k un entier compris entre 0 et n.La probabilité d'obtenir exactement k succès, et donc n − k échecs, est égale à :
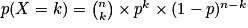
Exemple : En reprenant le sac avec les trois jetons, Kate fait 10 parties et gagne à chaque partie si elle pioche le jeton A. Calculons à présent la probabilité que Kate gagne exactement 7 parties.
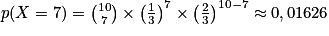 .
.Propriétés : Si
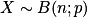 , on a trois formules qui donnent l'espérance, la variance et l'écart type de la variable aléatoire X en fonction des paramètres n et p : E(X) = np, V(X) = np(1 − p) et
, on a trois formules qui donnent l'espérance, la variance et l'écart type de la variable aléatoire X en fonction des paramètres n et p : E(X) = np, V(X) = np(1 − p) et 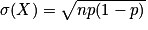 .
.Propriétés : Soient
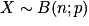 et k un entier compris entre 0 et n.
et k un entier compris entre 0 et n.La probabilité d'obtenir au plus k succès est égale à :
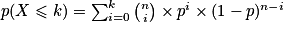
La probabilité d'obtenir au moins k succès est égale à :
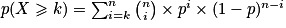
Remarque : En fonction du modèle de calculatrice, on peut effectuer une combinaison de touches qui permet de calculer directement p({X = k}) ou p({X
 k}) selon la question posée.
k}) selon la question posée.Exemple : En reprenant le sac avec les trois jetons, Kate fait 10 parties et gagne à chaque partie si elle pioche le jeton A. Calculons maintenant la probabilité que Kate gagne au maximum 7 parties.
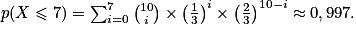
Représentation graphique :
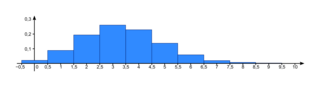
On peut représenter graphiquement la loi de probabilité d'une variable aléatoire discrète suivant une loi binomiale de paramètres n et p à l'aide d'un diagramme en barre ou d'un histogramme.
Le nombre de succès possibles est en abscisse, la probabilité de k succès est en ordonnée.
Exemple : En reprenant le sac avec les trois jetons, Kate fait toujours 10 parties et gagne à chaque partie si elle pioche le jeton A. On obtient alors le diagramme en bâtons ci-dessous :
 |
III. Comment peut-on utiliser Python en lien avec la loi binomiale ?
Soit α un réel de l'intervalle [0 ; 1]. Soient 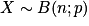 et k un entier compris entre 0 et n.
et k un entier compris entre 0 et n.
Recherche de seuil : On peut être amené à chercher le plus petit entier naturel k vérifiant p({X k})
k})  α.Voici un script contenant plusieurs fonctions utiles dans ce chapitre et répondant à la recherche :
α.Voici un script contenant plusieurs fonctions utiles dans ce chapitre et répondant à la recherche :
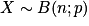 et k un entier compris entre 0 et n.
et k un entier compris entre 0 et n.Recherche de seuil : On peut être amené à chercher le plus petit entier naturel k vérifiant p({X
 k})
k})  α.Voici un script contenant plusieurs fonctions utiles dans ce chapitre et répondant à la recherche :
α.Voici un script contenant plusieurs fonctions utiles dans ce chapitre et répondant à la recherche : |
• La première fonction permet de calculer la factorielle de tout entier n.
• La deuxième fonction permet de calculer un coefficient binomial en connaissant n et k.
• La troisième fonction permet de calculer la probabilité d'obtenir k succès dans le cas d'une loi binomiale.
• La quatrième fonction permet de calculer la probabilité d'obtenir au plus k succès dans le cas d'une loi binomiale.
• La dernière fonction permet de déterminer le plus petit entier naturel k vérifiant p({X  k})
k})  α.
α.
 k})
k})  α.
α.La dernière fonction démarre avec la variable e à laquelle on affecte la valeur 0. Ensuite, à l'aide d'une boucle non bornée « Tant que », on va vérifier dans un premier temps si p({X  0}) < α. La variable e change alors de valeur et prend la valeur 1. Puis, on vérifie si on a p({X
0}) < α. La variable e change alors de valeur et prend la valeur 1. Puis, on vérifie si on a p({X  1}) < α, etc., jusqu'à ce que l'on trouve un entier k qui ne vérifie plus la condition p({X
1}) < α, etc., jusqu'à ce que l'on trouve un entier k qui ne vérifie plus la condition p({X  k}) < α.
k}) < α.
 0}) < α. La variable e change alors de valeur et prend la valeur 1. Puis, on vérifie si on a p({X
0}) < α. La variable e change alors de valeur et prend la valeur 1. Puis, on vérifie si on a p({X  1}) < α, etc., jusqu'à ce que l'on trouve un entier k qui ne vérifie plus la condition p({X
1}) < α, etc., jusqu'à ce que l'on trouve un entier k qui ne vérifie plus la condition p({X  k}) < α.
k}) < α.Histoire des mathématiques
La théorie des probabilités est une mathématisation de l'incertitude et du caractère imprévisible des phénomènes. Pendant l'Antiquité, le hasard n'était pas un objet d'étude et cette notion d'incertitude a longtemps été attribuée au destin ou aux divinités.Au xiie siècle, pour l'évaluation de contrats commerciaux, apparaît alors la notion de « risque » qui sera le point de départ de l'étude des probabilités. Mais la théorie des probabilités débute réellement au xviie siècle avec Fermat et Pascal, autour du problème des partis, c'est-à-dire la répartition inégale de points à la fin d'une partie que plusieurs joueurs ont convenu de ne pas achever. Huygens prend connaissance de cette discussion entre les deux mathématiciens et publie le premier traité sur la théorie probabiliste en 1657.
La parution de l'Ars Conjectandi de Jacques Bernoulli (1713), reprenant notamment les anciens travaux de Huygens, marque une rupture dans l'histoire des probabilités. On y trouve la première étude de la distribution binomiale, introduite dans le cadre d'un tirage sans remise pour un modèle d'urne, ainsi que divers problèmes combinatoires, notamment le binôme de Newton. Son traité contient également une description de l'estimation d'un phénomène aléatoire en s'appuyant sur des fréquences. C'est grâce aux fréquences qu'il établit l'un des résultats majeurs de cet ouvrage : son « théorème d'or », qui sera plus tard généralisé et deviendra le théorème actuel appelé « loi des grands nombres ».

