Dans ce troisième chapitre, l'inégalité de Bienaymé-Tchebychev explicite le rôle de la variance comme indicateur de dispersion. Tous ces outils se conjuguent pour établir l'inégalité de concentration pour la moyenne d'un échantillon d'une variable aléatoire, ce qui justifie l'apparition du facteur 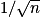 en théorie de l'estimation aperçue expérimentalement en classe de seconde, et ce qui va permettre d'aboutir à la démonstration de la loi des grands nombres, fondement de l'étude probabiliste.
en théorie de l'estimation aperçue expérimentalement en classe de seconde, et ce qui va permettre d'aboutir à la démonstration de la loi des grands nombres, fondement de l'étude probabiliste.
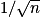 en théorie de l'estimation aperçue expérimentalement en classe de seconde, et ce qui va permettre d'aboutir à la démonstration de la loi des grands nombres, fondement de l'étude probabiliste.
en théorie de l'estimation aperçue expérimentalement en classe de seconde, et ce qui va permettre d'aboutir à la démonstration de la loi des grands nombres, fondement de l'étude probabiliste.I. Quelles sont les formules de majoration à connaître ?
Propriété : Inégalité de Bienaymé-TchebychevSoient X une variable aléatoire discrète, et δ un réel strictement positif.
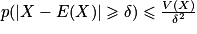 ou
ou 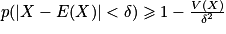 .
.Exemple 1 : Si, pour une certaine variable aléatoire X, E(X) = 10 et V(X) = 0,01, alors sans aucune indication particulière sur la loi de X, on sait que X prendra des valeurs entre 9,7 et 10,3 avec une probabilité supérieure à 0,88. Évidemment, si on connaît la loi de X, on peut calculer directement la valeur de cette probabilité.
Remarque : Ayant un caractère universel, l'inégalité de Bienaymé-Tchebychev possède cependant un défaut : les majorations obtenues ne sont pas très précises.
Exemple 2 : Soit X : B (10 ; 0,5). On a E(X) = 10 × 0,5 = 5 et V(X) = 10 × 0,5 × (1 − 0,5) = 2,5.
Soit δ = 4. On a alors :
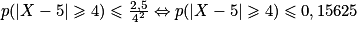 .
.Or
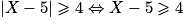 ou
ou 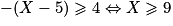 ou
ou 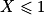 .
.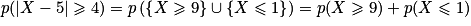
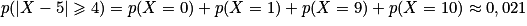 .
.Ainsi, l'inégalité p (|X − 5|
 4)
4)  0,15625 est vraie mais peu « précise ».
0,15625 est vraie mais peu « précise ».Propriété : Inégalité de concentration
Soient n un entier naturel non nul, (X1, X2, …, Xn) un échantillon d'une loi de probabilité d'espérance μ et de variance V, δ un réel strictement positif. On pose
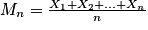 . On a :
. On a : 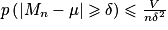 .
.Exemple : Combien de fois faut-il lancer une pièce équilibrée pour que la fréquence d'apparition de la face pile soit comprise strictement entre 0,45 et 0,55 avec une probabilité d'au moins 0,99 ?
Soit X : B (1 ; 0,5). On a : E(X) = p = 0,5 et V(X) = p(1 − p) = 0,25. Soient n un entier non nul et (X1, X2, …, Xn) un échantillon de taille n de la variable aléatoire X. On pose
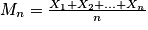 .
.On cherche l'entier n tel que p (0,45 < Mn < 0,55)
 0,99, c'est-à-dire p(|Mn − 0,5|
0,99, c'est-à-dire p(|Mn − 0,5|  0,05)
0,05)  0,01.
0,01.D'après l'inégalité de concentration, on a :
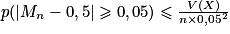 . D'où
. D'où 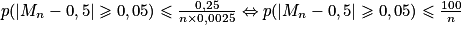 .
.Il suffit donc d'avoir
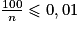 , c'est-à-dire n
, c'est-à-dire n  10 000.
10 000.Il suffit donc de lancer la pièce 10 000 fois pour que la fréquence d'apparition de la face pile soit comprise strictement entre 0,45 et 0,55 avec une probabilité d'au moins 0,99.
II. Que faut-il retenir sur la loi faible des grands nombres ?
Propriété : Loi faible des grands nombres
Soient n un entier naturel non nul, (X1, X2, …, Xn) un échantillon d'une loi de probabilité d'espérance μ, et δ un réel strictement positif. On pose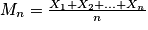 . On a :
. On a : 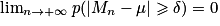 .
.
Remarques : On peut reformuler la propriété en : « Lorsque n est grand, sauf exception, la fréquence observée est proche de la probabilité. »
La limite de la propriété est équivalente à :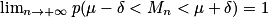 .
.
Démonstration : On sait que : E(Mn) = E(X) = μ et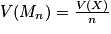 .
.
En utilisant l'inégalité de Bienaymé-Tchebychev, on a : pour tout réel strictement positif δ,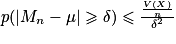 , soit
, soit 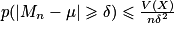 . Or
. Or 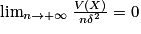 .
.
Donc, grâce au théorème des gendarmes, on obtient :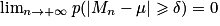 .
.
Exemple : La méthode de Monte-Carlo
On souhaite déterminer, à l'aide d'une simulation, une valeur approchée du nombre réel π.
On va pour cela imaginer une cible carrée ABCD de côté 1. On construit le quart de cercle de centre A et de rayon AB. On note E l'expérience aléatoire : « On lance une fléchette sur la cible ». On estime que la fléchette atteint toujours la cible et que la probabilité que la fléchette atteigne une zone est proportionnelle à l'aire de cette zone.
Si on pose A l'événement : « La fléchette touche le quart de disque », alors on peut calculer que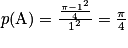 .
.
Pour déterminer une valeur approchée de π, on va simuler un très grand nombre de lancers de fléchettes, et on va calculer la proportion de fléchettes atteignant le quart de disque.
La loi faible des grands nombres nous garantit que plus la taille de l'échantillon est grande, plus la proportion des fléchettes atteignant le quart de disque va se rapprocher de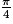 .
.
Voici un script permettant donc de déterminer une valeur approchée de π :
Soient n un entier naturel non nul, (X1, X2, …, Xn) un échantillon d'une loi de probabilité d'espérance μ, et δ un réel strictement positif. On pose
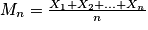 . On a :
. On a : 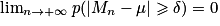 .
.Remarques : On peut reformuler la propriété en : « Lorsque n est grand, sauf exception, la fréquence observée est proche de la probabilité. »
La limite de la propriété est équivalente à :
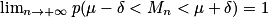 .
.Démonstration : On sait que : E(Mn) = E(X) = μ et
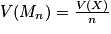 .
.En utilisant l'inégalité de Bienaymé-Tchebychev, on a : pour tout réel strictement positif δ,
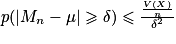 , soit
, soit 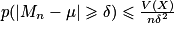 . Or
. Or 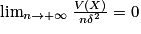 .
.Donc, grâce au théorème des gendarmes, on obtient :
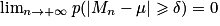 .
.Exemple : La méthode de Monte-Carlo
On souhaite déterminer, à l'aide d'une simulation, une valeur approchée du nombre réel π.
On va pour cela imaginer une cible carrée ABCD de côté 1. On construit le quart de cercle de centre A et de rayon AB. On note E l'expérience aléatoire : « On lance une fléchette sur la cible ». On estime que la fléchette atteint toujours la cible et que la probabilité que la fléchette atteigne une zone est proportionnelle à l'aire de cette zone.
Si on pose A l'événement : « La fléchette touche le quart de disque », alors on peut calculer que
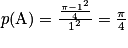 .
.Pour déterminer une valeur approchée de π, on va simuler un très grand nombre de lancers de fléchettes, et on va calculer la proportion de fléchettes atteignant le quart de disque.
La loi faible des grands nombres nous garantit que plus la taille de l'échantillon est grande, plus la proportion des fléchettes atteignant le quart de disque va se rapprocher de
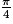 .
.Voici un script permettant donc de déterminer une valeur approchée de π :
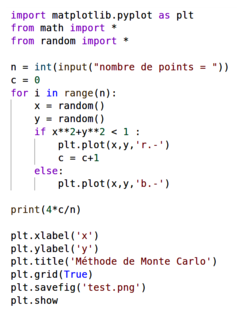 |
En entrant n = 10 000, on a obtenu une valeur approchée de 3,1276, et cette cible :
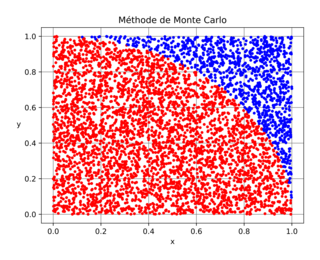 |
III. Comment peut-on simuler une variable aléatoire ?
Démarrage
Pour simuler une variable aléatoire, il faut donner la loi de probabilité de cette variable aléatoire, c'est-à-dire renseigner les valeurs qu'elle peut prendre et les probabilités associées. On utilisera des listes pour ces deux données.
Exemple : Simulation d'un lancer de dé. Ω = {1 ; 2 ; 3 ; 4 ; 5 ; 6}, avec pour chaque valeur une probabilité de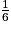 .
.
Exemple : Simulation d'un lancer de dé. Ω = {1 ; 2 ; 3 ; 4 ; 5 ; 6}, avec pour chaque valeur une probabilité de
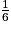 .
.• Le script simul permet, grâce à la fonction random, de simuler le choix aléatoire d'une valeur que peut prendre la variable aléatoire en tenant compte du poids des probabilités affectées.
• Le script un_echantillon permet, en affectant à la variable taille un entier non nul, de créer un échantillon. De même, le script N_echantillon permet de créer N échantillons.
 |
Paramètres
On crée trois scripts pour calculer l'espérance, la variance et l'écart type d'une variable aléatoire discrète.
La fonction N_moyennes permet de créer une liste qui, après avoir créé N échantillons, contient la moyenne de chaque échantillon.
La fonction ecarttype_des_N_moyennes permet de calculer l'écart type de la liste précédente.
La fonction N_moyennes permet de créer une liste qui, après avoir créé N échantillons, contient la moyenne de chaque échantillon.
La fonction ecarttype_des_N_moyennes permet de calculer l'écart type de la liste précédente.
 |
Écart et proportion
La fonction ecart1 permet de mesurer, après une simulation de N échantillons, l'écart entre l'écart type de la variable aléatoire X et l'écart type des moyennes de N échantillons.
Plus la variable « taille » est grande, plus cet écart est proche de 0.
La fonction proportion permet de déterminer la proportion des échantillons pour lesquels l'écart entre l'espérance de X et la moyenne de l'échantillon est inférieure ou égal à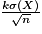 pour k un entier compris entre 1 et 3.
pour k un entier compris entre 1 et 3.
Plus la variable « taille » est grande, plus cet écart est proche de 0.
La fonction proportion permet de déterminer la proportion des échantillons pour lesquels l'écart entre l'espérance de X et la moyenne de l'échantillon est inférieure ou égal à
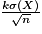 pour k un entier compris entre 1 et 3.
pour k un entier compris entre 1 et 3. |
Pour aller plus loin : Estimation
Fréquence
En statistique, la fréquence d'une valeur est le quotient entre son effectif et la taille de la population. On exprime cette fréquence sous la forme d'un pourcentage ou d'un nombre décimal.Intervalle de confiance et lien avec la fluctuation
Lorsque l'on veut connaître une information sur l'ensemble d'une population, il est compliqué d'interroger l'ensemble des personnes concernées. On constitue un échantillon représentatif, puis on étend les résultats obtenus.L'expérience montre que, lorsqu'on choisit un autre échantillon représentatif, on obtient des résultats assez proches. Aussi, pour avoir une meilleure approximation du résultat, on va donner un « intervalle de confiance » qui permet de limiter les effets de la fluctuation en fonction des échantillons.
« Au seuil de 95 % de la fréquence »
La phrase « au seuil de 95 % de la fréquence » signifie « avec une marge d'erreur de 5 % ».Intervalle de fluctuation au seuil de 95 % de la fréquence
Soit X une variable aléatoire qui suit la loi binomiale de paramètres n et p, X : B (n, p), avec 0 < p < 1, n 30, np > 5 et n(1 − p) > 5.
30, np > 5 et n(1 − p) > 5.On appelle intervalle asymptotique au seuil de 95 % de la fréquence l'intervalle :
![\left [ p-1,96\sqrt{\frac{p(1-p)}{n}};p+1,96\sqrt{\frac{p(1-p)}{n}} \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_15_m28.png)
Intervalle de confiance
Il s'agit de savoir comment estimer la proportion p d'individus dans une population ayant une propriété identique. Pour cela, on utilise la fréquence f observée sur un échantillon de la population.On appelle intervalle de confiance de la proportion p avec un niveau de confiance de 95 %, l'intervalle
![\left [ f-\frac{1}{\sqrt{n}};f+\frac{1}{\sqrt{n}} \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_15_m29.png) , où n est la taille de l'échantillon interrogé.
, où n est la taille de l'échantillon interrogé.Histoire des mathématiques
C'est grâce aux fréquences que Jacques Bernoulli établit l'un des résultats majeurs de son ouvrage l'Ars Conjectandi : son « théorème d'or », l'actuelle « loi des grands nombres ». Ce théorème, qui relie fréquences et probabilités, valide le principe de l'échantillonnage et est le premier exemple de « théorème limite » en théorie des probabilités.Les mathématiciens français et russe, Bienaymé et Tchebychev, ont démontré l'inégalité qui porte leur nom, en parlant de fréquences d'échantillons plutôt que de variables aléatoires. Ils fournissent ainsi la possibilité d'une démonstration plus simple de la loi des grands nombres.
Au début du xixe siècle, la modélisation des erreurs de mesure va devenir centrale pour faire de la statistique une science à part entière. Lagrange et Laplace ont développé une approche probabiliste de la théorie des erreurs. Gauss imagine une méthode des moindres carrés (après Legendre), qu'il applique avec succès à la prédiction de la position d'un astéroïde. Il y propose de comprendre l'écart type comme une « erreur moyenne à craindre ».
Finalement, l'introduction de méthodes statistiques en sociologie est l'œuvre du mathématicien et astronome belge Quételet dans les années 1830. Il réfléchit alors à la distribution de données autour de la moyenne. Ce procédé sera approfondi par l'anglais Galton, qui est l'inventeur de nombreuses méthodes statistiques couramment employées, comme l'étalonnage et la corrélation, qui lui ont notamment servi dans ses recherches sur la théorie de l'évolution.

