Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 4
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 4
Énoncé
14 points
La figure ci-dessous n'est pas représentée en vraie grandeur.
Les points C, B et E sont alignés.
Le triangle ABC est rectangle en A.
Le triangle BDC est rectangle en B.
Les points C, B et E sont alignés.
Le triangle ABC est rectangle en A.
Le triangle BDC est rectangle en B.
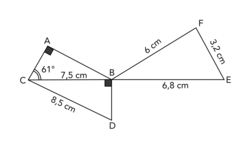 |
1. Montrer que la longueur BD est égale à 4 cm.
Pensez à utiliser le théorème de Pythagore.
2. Montrer que les triangles CBD et BFE sont semblables.
Deux triangles sont semblables si les longueurs des côtés de l'un sont proportionnelles aux longueurs des côtés de l'autre.
3. Sophie affirme que l'angle 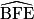 est un angle droit. A-t-elle raison ?
est un angle droit. A-t-elle raison ?
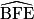 est un angle droit. A-t-elle raison ?
est un angle droit. A-t-elle raison ?Pensez à utiliser une propriété des triangles semblables.
4. Max affirme que l'angle  est un angle droit. A-t-il raison ?
est un angle droit. A-t-il raison ?
 est un angle droit. A-t-il raison ?
est un angle droit. A-t-il raison ?Pensez à utiliser une relation trigonométrique.
Corrigé
1. Dans le triangle BDC rectangle en B, d'après le théorème de Pythagore, on a : CD2 = BC2 + BD2.
On a donc : BD2 = CD2 − BC2 = 8,52 − 7,52 = 72,25 − 56,25 = 16 car CD = 8,5 cm et BC = 7,5 cm.
On en déduit BD =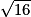 = 4 cm.
= 4 cm.
La longueur BD est égale à 4 cm.
On a donc : BD2 = CD2 − BC2 = 8,52 − 7,52 = 72,25 − 56,25 = 16 car CD = 8,5 cm et BC = 7,5 cm.
On en déduit BD =
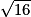 = 4 cm.
= 4 cm.La longueur BD est égale à 4 cm.
2. Deux triangles sont semblables si les longueurs des côtés de l'un sont proportionnelles aux longueurs des côtés de l'autre.
Montrons donc que les longueurs des côtés du triangle BFE sont proportionnelles aux longueurs des côtés du triangle CBD.
On remarque que :
Montrons donc que les longueurs des côtés du triangle BFE sont proportionnelles aux longueurs des côtés du triangle CBD.
On remarque que :
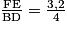 = 0,8 ;
= 0,8 ;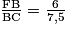 = 0,8 ;
= 0,8 ;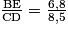 = 0,8.
= 0,8.
3. Les triangles CBD et BFE sont semblables et les angles de triangles semblables sont 2 à 2 égaux.
Le triangle BDC est rectangle en B, donc l'angle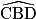 est un angle droit.
est un angle droit.
On en déduit que l'angle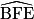 est aussi un angle droit, donc que Sophie a raison.
est aussi un angle droit, donc que Sophie a raison.
Le triangle BDC est rectangle en B, donc l'angle
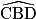 est un angle droit.
est un angle droit.On en déduit que l'angle
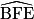 est aussi un angle droit, donc que Sophie a raison.
est aussi un angle droit, donc que Sophie a raison.4. Calculons la mesure de l'angle 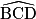 , pour ensuite obtenir la mesure de l'angle
, pour ensuite obtenir la mesure de l'angle 
Dans le triangle BDC rectangle en B, on a :
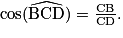
On a CB = 7,5 cm et CD = 8,5 cm, donc :
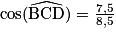 puis, à la calculatrice,
puis, à la calculatrice,
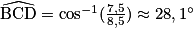 au dixième de degré près.
au dixième de degré près.
Finalement, =
= 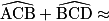
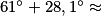
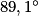 au dixième de degré près.
au dixième de degré près.
L'angle n'est donc pas un angle droit et Max a tort.
n'est donc pas un angle droit et Max a tort.
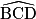 , pour ensuite obtenir la mesure de l'angle
, pour ensuite obtenir la mesure de l'angle 
Dans le triangle BDC rectangle en B, on a :
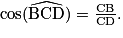
On a CB = 7,5 cm et CD = 8,5 cm, donc :
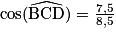 puis, à la calculatrice,
puis, à la calculatrice,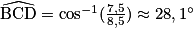 au dixième de degré près.
au dixième de degré près.Finalement,
 =
= 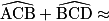
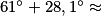
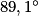 au dixième de degré près.
au dixième de degré près.L'angle
 n'est donc pas un angle droit et Max a tort.
n'est donc pas un angle droit et Max a tort.Corrigé
1. Dans le triangle BDC rectangle en B, d'après le théorème de Pythagore, on a : CD2 = BC2 + BD2.
On a donc : BD2 = CD2 − BC2 = 8,52 − 7,52 = 72,25 − 56,25 = 16 car CD = 8,5 cm et BC = 7,5 cm.
On en déduit BD =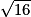 = 4 cm.
= 4 cm.
La longueur BD est égale à 4 cm.
On a donc : BD2 = CD2 − BC2 = 8,52 − 7,52 = 72,25 − 56,25 = 16 car CD = 8,5 cm et BC = 7,5 cm.
On en déduit BD =
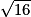 = 4 cm.
= 4 cm.La longueur BD est égale à 4 cm.
2. Deux triangles sont semblables si les longueurs des côtés de l'un sont proportionnelles aux longueurs des côtés de l'autre.
Montrons donc que les longueurs des côtés du triangle BFE sont proportionnelles aux longueurs des côtés du triangle CBD.
On remarque que :
Montrons donc que les longueurs des côtés du triangle BFE sont proportionnelles aux longueurs des côtés du triangle CBD.
On remarque que :
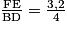 = 0,8 ;
= 0,8 ;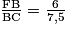 = 0,8 ;
= 0,8 ;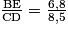 = 0,8.
= 0,8.
3. Les triangles CBD et BFE sont semblables et les angles de triangles semblables sont 2 à 2 égaux.
Le triangle BDC est rectangle en B, donc l'angle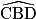 est un angle droit.
est un angle droit.
On en déduit que l'angle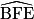 est aussi un angle droit, donc que Sophie a raison.
est aussi un angle droit, donc que Sophie a raison.
Le triangle BDC est rectangle en B, donc l'angle
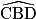 est un angle droit.
est un angle droit.On en déduit que l'angle
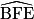 est aussi un angle droit, donc que Sophie a raison.
est aussi un angle droit, donc que Sophie a raison.4. Calculons la mesure de l'angle 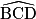 , pour ensuite obtenir la mesure de l'angle
, pour ensuite obtenir la mesure de l'angle 
Dans le triangle BDC rectangle en B, on a :
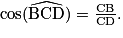
On a CB = 7,5 cm et CD = 8,5 cm, donc :
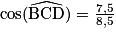 puis, à la calculatrice,
puis, à la calculatrice,
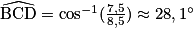 au dixième de degré près.
au dixième de degré près.
Finalement, =
= 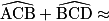
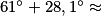
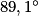 au dixième de degré près.
au dixième de degré près.
L'angle n'est donc pas un angle droit et Max a tort.
n'est donc pas un angle droit et Max a tort.
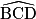 , pour ensuite obtenir la mesure de l'angle
, pour ensuite obtenir la mesure de l'angle 
Dans le triangle BDC rectangle en B, on a :
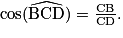
On a CB = 7,5 cm et CD = 8,5 cm, donc :
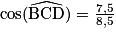 puis, à la calculatrice,
puis, à la calculatrice,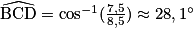 au dixième de degré près.
au dixième de degré près.Finalement,
 =
= 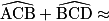
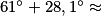
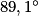 au dixième de degré près.
au dixième de degré près.L'angle
 n'est donc pas un angle droit et Max a tort.
n'est donc pas un angle droit et Max a tort.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 4
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 4

