Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 1
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 1
Énoncé
11 points
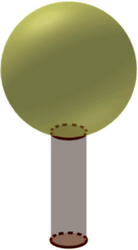
Le gros globe de cristal est un trophée attribué au vainqueur de la coupe du monde de ski.
Ce trophée pèse 9 kg et mesure 46 cm de hauteur.
Ce trophée pèse 9 kg et mesure 46 cm de hauteur.
 |
1.
Le biathlète français Martin Fourcade a remporté le sixième gros globe de cristal de sa carrière en 2017 à PyeonChang en Corée du Sud.
Donner approximativement la latitude et la longitude de ce lieu repéré sur la carte ci-dessous.
Donner approximativement la latitude et la longitude de ce lieu repéré sur la carte ci-dessous.
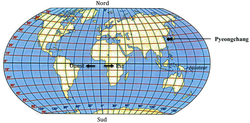 |
À partir des méridiens et des parallèles, on définit pour chaque point sur la Terre :
- sa longitude à partir du méridien de référence, celui de Greenwich ;
- sa latitude à partir de la parallèle de référence, qui est PyeonChang.
2.
On considère que ce globe est composé d'un cylindre en cristal de diamètre 6 cm, surmonté d'une boule de cristal. Voir le schéma ci-dessous.
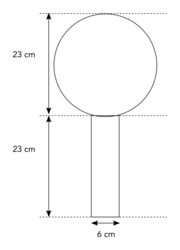 |
Montrer qu'une valeur approchée du volume de la boule de ce trophée est de 6 371 cm3.
Pour le calcul du volume de la boule de cristal, ne confondez pas diamètre et rayon.
3.
Marie affirme que le volume de la boule de cristal représente environ 90 % du volume total du trophée.
A-t-elle raison ?
Rappels :
A-t-elle raison ?
Rappels :
- volume d'une boule de rayon R : V =
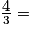 πR3 ;
πR3 ; - volume d'un cylindre de rayon r et de hauteur h : V = πr2h.
Commencez par calculer le volume du cylindre en cristal pour pouvoir calculer le volume total du trophée.
Corrigé
1. D'après la carte, la ville de PyeonChang en Corée du Sud a approximativement pour longitude 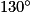 Est et pour latitude
Est et pour latitude 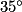 Nord.
Nord.
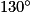 Est et pour latitude
Est et pour latitude 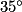 Nord.
Nord.2. Le rayon de la boule de cristal est de R = 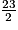 = 11,5 cm.
= 11,5 cm.
Le volume de cette boule de cristal de rayon R est donc :
V =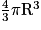 =
= 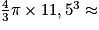 6 371 cm3 à l'unité près.
6 371 cm3 à l'unité près.
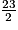 = 11,5 cm.
= 11,5 cm.Le volume de cette boule de cristal de rayon R est donc :
V =
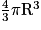 =
= 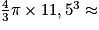 6 371 cm3 à l'unité près.
6 371 cm3 à l'unité près.3. Calculons le volume du cylindre en cristal qui a pour rayon de base r = 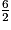 = 3 cm et pour hauteur h = 23 cm :
= 3 cm et pour hauteur h = 23 cm :
V' = π × r2 × h = π × 32 × 23 = 207π 650 cm3 à l'unité près.
650 cm3 à l'unité près.
Le volume total de ce trophée est donc de V + V' 6 371 + 650
6 371 + 650  7 021 cm3 à l'unité près.
7 021 cm3 à l'unité près.
Par rapport au volume total du trophée, le volume de la boule de cristal représente donc :
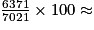 90,7 % au dixième près.
90,7 % au dixième près.
Marie a donc raison quand elle affirme que le volume de la boule de cristal représente environ 90 % du volume total du trophée.
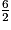 = 3 cm et pour hauteur h = 23 cm :
= 3 cm et pour hauteur h = 23 cm :V' = π × r2 × h = π × 32 × 23 = 207π
 650 cm3 à l'unité près.
650 cm3 à l'unité près.Le volume total de ce trophée est donc de V + V'
 6 371 + 650
6 371 + 650  7 021 cm3 à l'unité près.
7 021 cm3 à l'unité près.Par rapport au volume total du trophée, le volume de la boule de cristal représente donc :
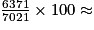 90,7 % au dixième près.
90,7 % au dixième près.Marie a donc raison quand elle affirme que le volume de la boule de cristal représente environ 90 % du volume total du trophée.
Corrigé
1. D'après la carte, la ville de PyeonChang en Corée du Sud a approximativement pour longitude 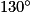 Est et pour latitude
Est et pour latitude 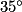 Nord.
Nord.
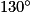 Est et pour latitude
Est et pour latitude 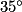 Nord.
Nord.2. Le rayon de la boule de cristal est de R = 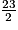 = 11,5 cm.
= 11,5 cm.
Le volume de cette boule de cristal de rayon R est donc :
V =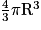 =
= 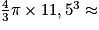 6 371 cm3 à l'unité près.
6 371 cm3 à l'unité près.
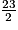 = 11,5 cm.
= 11,5 cm.Le volume de cette boule de cristal de rayon R est donc :
V =
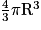 =
= 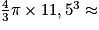 6 371 cm3 à l'unité près.
6 371 cm3 à l'unité près.3. Calculons le volume du cylindre en cristal qui a pour rayon de base r = 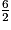 = 3 cm et pour hauteur h = 23 cm :
= 3 cm et pour hauteur h = 23 cm :
V' = π × r2 × h = π × 32 × 23 = 207π 650 cm3 à l'unité près.
650 cm3 à l'unité près.
Le volume total de ce trophée est donc de V + V' 6 371 + 650
6 371 + 650  7 021 cm3 à l'unité près.
7 021 cm3 à l'unité près.
Par rapport au volume total du trophée, le volume de la boule de cristal représente donc :
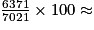 90,7 % au dixième près.
90,7 % au dixième près.
Marie a donc raison quand elle affirme que le volume de la boule de cristal représente environ 90 % du volume total du trophée.
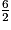 = 3 cm et pour hauteur h = 23 cm :
= 3 cm et pour hauteur h = 23 cm :V' = π × r2 × h = π × 32 × 23 = 207π
 650 cm3 à l'unité près.
650 cm3 à l'unité près.Le volume total de ce trophée est donc de V + V'
 6 371 + 650
6 371 + 650  7 021 cm3 à l'unité près.
7 021 cm3 à l'unité près.Par rapport au volume total du trophée, le volume de la boule de cristal représente donc :
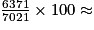 90,7 % au dixième près.
90,7 % au dixième près.Marie a donc raison quand elle affirme que le volume de la boule de cristal représente environ 90 % du volume total du trophée.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 1
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2018, exercice 1

