Énoncé
6 points
Agnès envisage de peindre la façade de son hangar.
Information 1. Caractéristiques de la peinture utilisée.
Renseignements concernant un pot de peinture
Renseignements concernant un pot de peinture
 |
* Une seule couche de peinture suffit.
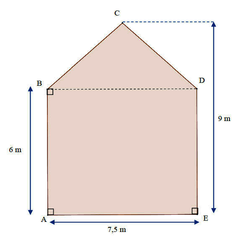
Information 2. Schéma de la façade.
(Le schéma n'est pas à l'échelle)
La zone grisée est la zone à peindre.
(Le schéma n'est pas à l'échelle)
La zone grisée est la zone à peindre.
 |
1.
Quel est le montant minimum à prévoir pour l'achat des pots de peinture ?
Calculez l'aire du polygone ABCDE, puis déduisez-en le nombre (entier) de pots de peinture qu'Agnès doit acheter pour peindre cette surface.
Rappelez-vous que l'aire d'un triangle de la longueur de base B et de hauteur associée h est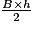 .
.
Rappelez-vous que l'aire d'un triangle de la longueur de base B et de hauteur associée h est
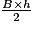 .
.2.
Agnès achète la peinture et tout le matériel dont elle a besoin pour ses travaux. Le montant total de la facture est de 343,50 €.
Le magasin lui propose de régler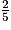 de la facture aujourd'hui et le reste en trois mensualités identiques.
de la facture aujourd'hui et le reste en trois mensualités identiques.
Quel sera le montant de chaque mensualité ?
Le magasin lui propose de régler
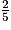 de la facture aujourd'hui et le reste en trois mensualités identiques.
de la facture aujourd'hui et le reste en trois mensualités identiques.Quel sera le montant de chaque mensualité ?
Commencez par calculer le montant qu'Agnès règle aujourd'hui, puis déduisez-en le montant restant à payer en trois mensualités. Vous devez trouver un montant proche de 70 € pour chaque mensualité.
Une autre méthode plus rapide consiste à exprimer chaque mensualité sous la forme d'une fraction de 343,50 € et d'effectuer le calcul.
Une autre méthode plus rapide consiste à exprimer chaque mensualité sous la forme d'une fraction de 343,50 € et d'effectuer le calcul.
Corrigé
1.
Commençons par calculer l'aire du polygone ABCDE, qui est la somme de l'aire du rectangle ABDE et du triangle BCD.
L'aire du rectangle ABDE est AB × AE = 6 × 7,5 = 45 cm2.
L'aire du triangle BCD est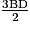 =
= 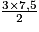 = 11,25 cm2, car la hauteur de ce triangle est égale à 9 − 6 = 3 cm.
= 11,25 cm2, car la hauteur de ce triangle est égale à 9 − 6 = 3 cm.
L'aire du polygone ABCDE est donc 45 + 11,25 = 56,25 cm2.
Calculons ensuite le nombre de pots de peinture nécessaire pour peindre cette surface.
Chaque pot de peinture permet de peindre 24 m2 de surface et :
2 × 24 = 48 < 56,25 < 3 × 24 = 72, donc Agnès doit acheter 3 pots de peinture pour peindre cette surface.
Le montant minimum à prévoir pour l'achat de pot de peinture est donc de 3 × 103,45 = 310,35 €.
L'aire du rectangle ABDE est AB × AE = 6 × 7,5 = 45 cm2.
L'aire du triangle BCD est
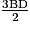 =
= 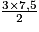 = 11,25 cm2, car la hauteur de ce triangle est égale à 9 − 6 = 3 cm.
= 11,25 cm2, car la hauteur de ce triangle est égale à 9 − 6 = 3 cm. L'aire du polygone ABCDE est donc 45 + 11,25 = 56,25 cm2.
Calculons ensuite le nombre de pots de peinture nécessaire pour peindre cette surface.
Chaque pot de peinture permet de peindre 24 m2 de surface et :
2 × 24 = 48 < 56,25 < 3 × 24 = 72, donc Agnès doit acheter 3 pots de peinture pour peindre cette surface.
Le montant minimum à prévoir pour l'achat de pot de peinture est donc de 3 × 103,45 = 310,35 €.
2.
Première méthode :
Aujourd'hui, Agnès règle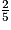 × 343,50 =
× 343,50 = 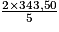 =
= 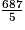 = 137,40 €.
= 137,40 €.
Il reste donc à régler en 3 mensualités identiques la somme de 343,50 − 137,40 = 206,10 €.
Le montant de chaque mensualité sera donc de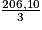 = 68,70 €.
= 68,70 €.
Deuxième méthode :
Agnès règle aujourd'hui deux cinquièmes de la facture, donc les trois mensualités identiques de la somme restant à payer représentent trois cinquièmes de la facture.
Le montant de chaque mensualité est donc d'un cinquième de la facture, c'est-à-dire :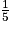 × 343,50 =
× 343,50 = 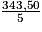 = 68,70 €.
= 68,70 €.
Aujourd'hui, Agnès règle
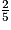 × 343,50 =
× 343,50 = 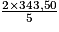 =
= 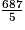 = 137,40 €.
= 137,40 €. Il reste donc à régler en 3 mensualités identiques la somme de 343,50 − 137,40 = 206,10 €.
Le montant de chaque mensualité sera donc de
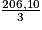 = 68,70 €.
= 68,70 €. Deuxième méthode :
Agnès règle aujourd'hui deux cinquièmes de la facture, donc les trois mensualités identiques de la somme restant à payer représentent trois cinquièmes de la facture.
Le montant de chaque mensualité est donc d'un cinquième de la facture, c'est-à-dire :
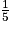 × 343,50 =
× 343,50 = 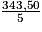 = 68,70 €.
= 68,70 €. 
