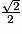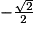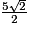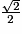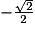Parmi l'ensemble des fonctions étudiées, les fonctions sinus et cosinus présentent des particularités spécifiques, notamment la périodicité. L'étude de ces fonctions sur la période (un intervalle) va permettre d'obtenir la représentation graphique de toute la fonction. On pourra revoir graphiquement les propriétés du sinus et du cosinus d'un angle étudiées en classe de Seconde et de Première.
1. Définition, dérivation
La fonction cosinus, notée cos, est la fonction qui à tout réel x associe le nombre réel cosx.La fonction sinus, notée sin, est la fonction qui à tout réel x associe le nombre réel sinx.
Propriétés : les fonctions sinus et cosinus sont dérivables sur l'ensemble des réels.
Pour tout réel x : cos'(x) = − sin(x) et cos'(ax + b) = − a sin(ax + b).
Pour tout réel x : sin'(x) = cos(x) et sin'(ax + b) = a cos(ax + b).
Exercice n°1Exercice n°2Exercice n°3
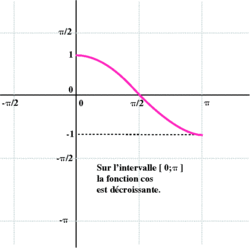
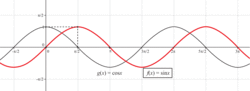
2. Fonctions sinus et cosinus sur l'intervalle [0 ; π]
La fonction cosinus
 |
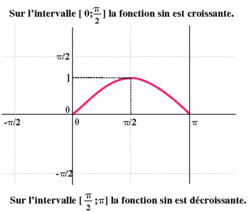
La fonction sinus
 |
3. Parité, périodicité des courbes représentatives des fonctions sinus et cosinus
Pour tout réel x, on a cos(−x) = cos x donc la fonction cosinus est paire.
Pour tout réel x, on a sin(−x) = −sin x donc la fonction sinus est impaire.
Pour tout réel x, on a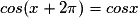 et
et 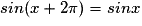 .
.
Donc les fonctions sinus et cosinus sont périodiques de période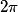 .
.
Pour tout réel x, on a sin(−x) = −sin x donc la fonction sinus est impaire.
Pour tout réel x, on a
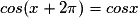 et
et 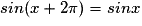 .
.Donc les fonctions sinus et cosinus sont périodiques de période
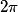 .
. |
4. Valeurs remarquables :
| Angle α | 0 | 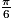 | 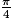 | 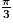 | 1 |
| cos (α) | 1 | 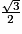 | 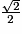 | 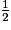 | 0 |
| sin (α) | 0 | 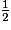 | 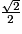 | 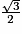 | 1 |
Démonstration :
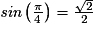
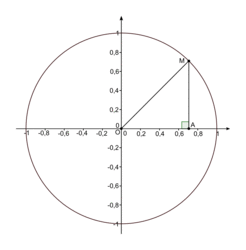
On place le point M sur le cercle trigonométrique tel que M représente le réel
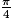 . Alors une mesure en radians de l'angle orienté
. Alors une mesure en radians de l'angle orienté 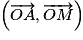 est
est 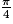 . Soit A le projeté orthogonal de M sur l'axe des abscisses. OAM est donc rectangle iscocèle en A. On a d'après le théorème de Pythagore :
. Soit A le projeté orthogonal de M sur l'axe des abscisses. OAM est donc rectangle iscocèle en A. On a d'après le théorème de Pythagore :OM2 = OA2 + AM2
Or OA = AM et OM = 1 donc :
12 = 2 × OA2
Ainsi
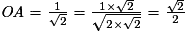 .
. |
À retenir
- cos'(ax + b) = −a sin(ax + b) et sin'(ax + b) = a cos(ax + b).
- Les fonctions sinus et cosinus sont périodiques de période
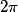 .
.
Exercice n°1
Quelle est la dérivée de la fonction définie par f(x) = 3 sin (4x + 5) et dérivable sur l'ensemble des réels ?
Cochez la bonne réponse.
| ||
| ||
|
On sait que la dérivée de sin (4x +5) est égale à 4 cos (4x + 5).
Donc f'(x) = 12 cos (4x + 5).
Donc f'(x) = 12 cos (4x + 5).
Exercice n°2
Quelle est la dérivée de la fonction définie par f(x) = 3 cos (4x + 5) et dérivable sur l'ensemble des réels ?
Cochez la bonne réponse.
| ||
| ||
|
On sait que la dérivée de cos(4x + 5) est égale à −4 sin (4x + 5).
Donc f'(x) = −12 sin (4x + 5).
Donc f'(x) = −12 sin (4x + 5).
Exercice n°3
À quoi est égale 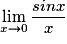 ?
?
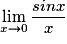 ?
? Cochez la bonne réponse.
| ||
| ||
|
On a : 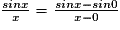 .
.
Donc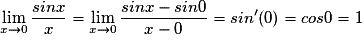
Pour calculer cette limite, on utilise le nombre dérivé de la fonction sin en 0, il est égal à cos 0, c'est-à-dire 1.
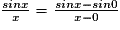 .
.Donc
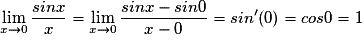
Pour calculer cette limite, on utilise le nombre dérivé de la fonction sin en 0, il est égal à cos 0, c'est-à-dire 1.
Exercice n°4
On considère la fonction définie sur l'ensemble des réels par : 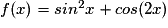 .
.
Que peut-on dire sur la parité de cette fonction ?
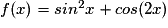 .
.Que peut-on dire sur la parité de cette fonction ?
Cochez la bonne réponse.
| ||
| ||
|
Pour tout réel x on a : 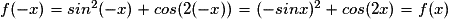 .
.
Donc la fonction f est paire.
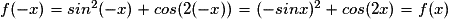 .
. Donc la fonction f est paire.
Exercice n°5
Quelles sont les solutions dans l'ensemble des réels de l'équation 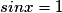 ?
?
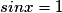 ?
? Cochez la bonne réponse.
| ||
| ||
|
On sait que 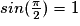 , la fonction sinus étant périodique de période
, la fonction sinus étant périodique de période 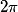 on aura :
on aura : 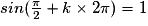 avec k nombre réel.
avec k nombre réel.
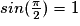 , la fonction sinus étant périodique de période
, la fonction sinus étant périodique de période 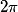 on aura :
on aura : 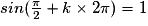 avec k nombre réel.
avec k nombre réel.Exercice n°6
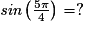
Cochez la bonne réponse.
| ||
| ||
| ||
|
Exercice n°7
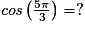
Cochez la bonne réponse.
| ||
| ||
| ||
|
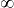
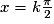 avec k nombre réel
avec k nombre réel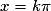 avec k nombre réel
avec k nombre réel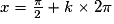 avec k nombre réel
avec k nombre réel