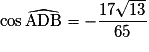Les vecteurs sont des objets géométriques sur lesquels on peut effectuer des calculs : on sait les additionner, les multiplier par un réel. Ici, on définit une nouvelle opération sur les vecteurs : le produit scalaire. À la différence des sommes de vecteurs ou des produits de vecteurs par un réel, le produit scalaire de deux vecteurs est un nombre réel.
Les applications du produit scalaire sont nombreuses tant en physique (particulièrement en mécanique) qu'en mathématiques : le produit scalaire fournissant une caractérisation particulièrement simple de l'orthogonalité de deux vecteurs, il permet d'établir de nombreuses relations sur les distances et les angles.
Les applications du produit scalaire sont nombreuses tant en physique (particulièrement en mécanique) qu'en mathématiques : le produit scalaire fournissant une caractérisation particulièrement simple de l'orthogonalité de deux vecteurs, il permet d'établir de nombreuses relations sur les distances et les angles.
1. Quelles sont les différentes manières de calculer un produit scalaire ?
• Le produit scalaire de deux vecteurs est un réel qui peut se calculer de quatre manières :
– le produit scalaire de deux vecteurs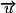 et
et 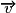 est le nombre réel noté
est le nombre réel noté 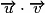 défini par
défini par ![\overrightarrow{u}\cdot\overrightarrow{v} = \frac{1}{2}\left[ {\left\| {\overrightarrow{u} + \overrightarrow{v}} \right\| ^2 - \left\| {\overrightarrow{u}} \right\| ^2 - \left\| {\overrightarrow{v}} \right\| ^2 } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_12_m4.png) ;
;
–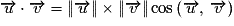 ou, si
ou, si  est une mesure de l'angle géométrique associé à
est une mesure de l'angle géométrique associé à 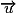 et
et 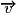 , on a aussi :
, on a aussi : 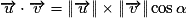 ;
;
– dans un repère orthonormal, si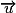 et
et 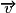 ont pour coordonnées respectives (x ; y) et (x' ; y'), alors
ont pour coordonnées respectives (x ; y) et (x' ; y'), alors 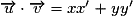 ;
;
– si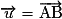 et
et 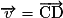 et si les points C et D se projettent orthogonalement en C' et D' sur la droite (AB) alors
et si les points C et D se projettent orthogonalement en C' et D' sur la droite (AB) alors 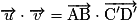 .
.
– le produit scalaire de deux vecteurs
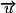 et
et 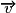 est le nombre réel noté
est le nombre réel noté 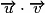 défini par
défini par ![\overrightarrow{u}\cdot\overrightarrow{v} = \frac{1}{2}\left[ {\left\| {\overrightarrow{u} + \overrightarrow{v}} \right\| ^2 - \left\| {\overrightarrow{u}} \right\| ^2 - \left\| {\overrightarrow{v}} \right\| ^2 } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_12_m4.png) ;
;–
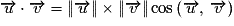 ou, si
ou, si  est une mesure de l'angle géométrique associé à
est une mesure de l'angle géométrique associé à 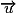 et
et 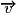 , on a aussi :
, on a aussi : 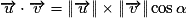 ;
;– dans un repère orthonormal, si
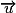 et
et 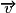 ont pour coordonnées respectives (x ; y) et (x' ; y'), alors
ont pour coordonnées respectives (x ; y) et (x' ; y'), alors 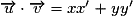 ;
;– si
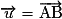 et
et 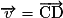 et si les points C et D se projettent orthogonalement en C' et D' sur la droite (AB) alors
et si les points C et D se projettent orthogonalement en C' et D' sur la droite (AB) alors 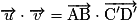 .
.• Pour calculer un produit scalaire en géométrie non analytique, on utilise la relation de Chasles pour décomposer les vecteurs et se ramener ainsi à des calculs de produits scalaires sur des vecteurs orthogonaux ou colinéaires.
2. Quels sont les cas particuliers à connaître ?
• Il faut connaître trois produits scalaires particuliers :
– si l'un des deux vecteurs est nul, leur produit scalaire est nul ;
– deux vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul ;
– si deux vecteurs non nuls sont colinéaires, alors :
s'ils sont de même sens,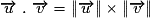 ;
;
s'ils sont de sens contraire,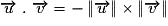 .
.
– si l'un des deux vecteurs est nul, leur produit scalaire est nul ;
– deux vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul ;
– si deux vecteurs non nuls sont colinéaires, alors :
s'ils sont de même sens,
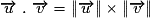 ;
;s'ils sont de sens contraire,
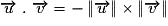 .
.• Pour montrer que deux droites du plan d et d' de vecteurs directeurs respectifs 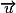 et
et 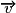 sont orthogonales, on montre que
sont orthogonales, on montre que 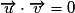 .
.
Exercice n°1Exercice n°2
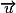 et
et 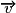 sont orthogonales, on montre que
sont orthogonales, on montre que 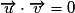 .
.Exercice n°1Exercice n°2
3. Quelles sont les propriétés du produit scalaire ?
Pour effectuer des calculs vectoriels avec des produits scalaires, on utilise les propriétés suivantes :–
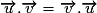 (on dit que le produit scalaire est symétrique) ;
(on dit que le produit scalaire est symétrique) ;–
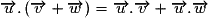 ;
;–pour tout réel k,
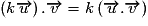 ;
;–le carré scalaire de
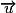 est :
est : 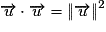 .
.4. Comment utilise-t-on le produit scalaire pour déterminer des équations de droites ou de cercles ?
• On appelle vecteur normal à une droite D, de vecteur directeur 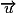 , tout vecteur non nul
, tout vecteur non nul 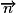 orthogonal à
orthogonal à 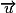 . La droite D passant par A et de vecteur normal
. La droite D passant par A et de vecteur normal 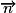 est l'ensemble des points M du plan tels que
est l'ensemble des points M du plan tels que 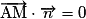 .
.
Cette propriété permet de donner une équation cartésienne de la droite D : dans un repère orthonormal, une droite de vecteur normal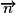 de coordonnées (a ; b) a une équation de la forme
de coordonnées (a ; b) a une équation de la forme 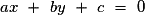 .
.
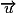 , tout vecteur non nul
, tout vecteur non nul 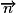 orthogonal à
orthogonal à 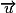 . La droite D passant par A et de vecteur normal
. La droite D passant par A et de vecteur normal 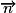 est l'ensemble des points M du plan tels que
est l'ensemble des points M du plan tels que 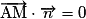 .
.Cette propriété permet de donner une équation cartésienne de la droite D : dans un repère orthonormal, une droite de vecteur normal
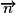 de coordonnées (a ; b) a une équation de la forme
de coordonnées (a ; b) a une équation de la forme 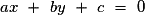 .
.• La notion de produit scalaire fournit deux méthodes pour déterminer une équation de cercle :
– dans le cas où on connaît un diamètre [AB], on utilise la propriété :
le cercle de diamètre [AB] est l'ensemble des points M du plan tels que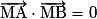 ;
;
– dans le cas où on connaît le centre I et le rayon R, on utilise la définition : le cercle de centre I et de rayon R est l'ensemble des points M du plan tels que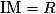 .
.
On montre alors que, dans un repère orthonormal, tout cercle a une équation de la forme :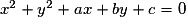 .
.
– dans le cas où on connaît un diamètre [AB], on utilise la propriété :
le cercle de diamètre [AB] est l'ensemble des points M du plan tels que
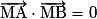 ;
;– dans le cas où on connaît le centre I et le rayon R, on utilise la définition : le cercle de centre I et de rayon R est l'ensemble des points M du plan tels que
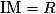 .
.On montre alors que, dans un repère orthonormal, tout cercle a une équation de la forme :
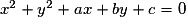 .
.5. Quelles relations métriques dans le triangle doit-on connaître ?
La notion de produit scalaire permet de démontrer quatre relations métriques dans le triangle qui permettent de calculer des distances ou des angles.• La relation d'Al-Kashi.
Soit ABC un triangle quelconque, alors :
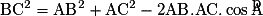 .
.
On remarque que si le triangle ABC est rectangle en A, on retrouve ainsi le théorème de Pythagore. C'est pourquoi la relation d'Al-Kashi est parfois appelée théorème de Pythagore généralisé.
Démonstration du théorème d'Al-Kashi :
Soit un triangle ABC quelconque. On note  l'angle géométrique BAC.
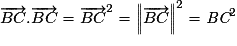
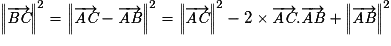
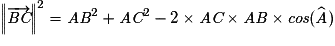
Démonstration :
Soit A et B deux points distincts du plan. On cherche l'ensemble des points M vérifiant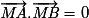 .
.
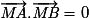 signifie que (MA) et (MB) sont perpendiculaires donc AMB rectangle en M.
signifie que (MA) et (MB) sont perpendiculaires donc AMB rectangle en M.
Donc M appartient au cercle de diamètre [AB].
Soit ABC un triangle quelconque, alors :
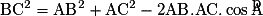 .
.On remarque que si le triangle ABC est rectangle en A, on retrouve ainsi le théorème de Pythagore. C'est pourquoi la relation d'Al-Kashi est parfois appelée théorème de Pythagore généralisé.
Démonstration du théorème d'Al-Kashi :
Soit un triangle ABC quelconque. On note  l'angle géométrique BAC.
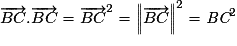
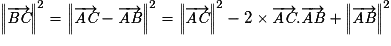
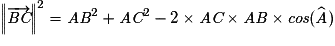
Démonstration :
Soit A et B deux points distincts du plan. On cherche l'ensemble des points M vérifiant
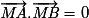 .
.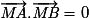 signifie que (MA) et (MB) sont perpendiculaires donc AMB rectangle en M.
signifie que (MA) et (MB) sont perpendiculaires donc AMB rectangle en M.Donc M appartient au cercle de diamètre [AB].
À retenir
• Il faut absolument penser que le produit scalaire de deux vecteurs est un réel : dans un repère orthonormal, si 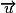 et
et 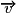 ont pour coordonnées respectives
ont pour coordonnées respectives 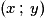 et
et 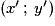 , alors :
, alors : 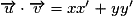 .
.
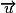 et
et 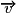 ont pour coordonnées respectives
ont pour coordonnées respectives 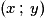 et
et 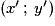 , alors :
, alors : 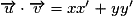 .
.• Deux vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul.
Cette propriété s'utilise pour étudier les positions relatives de droites du plan.
Cette propriété s'utilise pour étudier les positions relatives de droites du plan.
• Dans un triangle, si on connaît les longueurs des trois côtés, ou les longueurs de deux côtés et l'angle compris entre ces deux côtés, ou encore la longueur d'un côté et les deux angles adjacents à ce côté, alors, en utilisant les relations métriques, on est capable de calculer tous les éléments manquants (côtés et angles inconnus, aire du triangle).
Exercice n°1
Cochez la bonne réponse.
Parmi les propositions suivantes, laquelle est correcte ?
Cochez la bonne réponse.
| ||
| ||
|
Si deux vecteurs sont égaux, on peut remplacer l'un par l'autre sans changer la valeur du produit scalaire.
Mais deux vecteurs non nuls et orthogonaux ont un produit scalaire nul et le produit scalaire de deux vecteurs colinéaires et de sens contraire est négatif.
Mais deux vecteurs non nuls et orthogonaux ont un produit scalaire nul et le produit scalaire de deux vecteurs colinéaires et de sens contraire est négatif.
Exercice n°2
Cochez la bonne réponse.
La droite D, d'équation 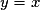 , est tangente à un cercle centré en A de coordonnées (2 ; 4).
, est tangente à un cercle centré en A de coordonnées (2 ; 4).
Quel est le rayon de ce cercle ?
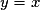 , est tangente à un cercle centré en A de coordonnées (2 ; 4).
, est tangente à un cercle centré en A de coordonnées (2 ; 4).Quel est le rayon de ce cercle ?
Cochez la bonne réponse.
| ||
| ||
|
• Soit H le point de contact de la droite D et du cercle. Alors la droite (AH) est perpendiculaire à la droite D en H et le rayon du cercle est AH.
Comme H appartient à la droite D d'équation y = x, ses coordonnées sont de la forme (x ; x).
Les coordonnées du vecteur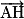 sont
sont 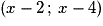 .
.
Comme H appartient à la droite D d'équation y = x, ses coordonnées sont de la forme (x ; x).
Les coordonnées du vecteur
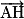 sont
sont 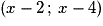 .
.• La droite D admet pour vecteur directeur le vecteur  de coordonnées (1 ; 1).
de coordonnées (1 ; 1).
La droite (AH) est perpendiculaire à la droite D en H si et seulement si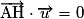 soit
soit 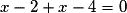 .
.
On en déduit que les coordonnées de H sont (3 ; 3).
Le rayon du cercle est donc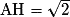 .
.
 de coordonnées (1 ; 1).
de coordonnées (1 ; 1).La droite (AH) est perpendiculaire à la droite D en H si et seulement si
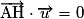 soit
soit 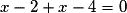 .
.On en déduit que les coordonnées de H sont (3 ; 3).
Le rayon du cercle est donc
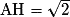 .
.Exercice n°3
Cochez la bonne réponse.
Parmi les propositions suivantes, laquelle est correcte ?
Cochez la bonne réponse.
| ||
| ||
|
• On transforme les deux équations en :
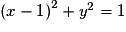 et
et 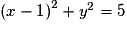 .
.
Ces deux cercles ont le même centre, de coordonnées (1 ; 0).
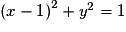 et
et 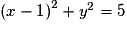 .
.Ces deux cercles ont le même centre, de coordonnées (1 ; 0).
• La proposition : « Si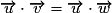 , alors
, alors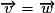 . » est fausse.
. » est fausse.
On peut seulement dire que les vecteurs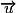 et
et  sont orthogonaux.
sont orthogonaux.
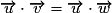 , alors
, alors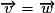 . » est fausse.
. » est fausse.On peut seulement dire que les vecteurs
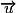 et
et  sont orthogonaux.
sont orthogonaux.• La proposition : « Si ABC est un triangle équilatéral de côté 4, alors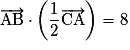 . » est fausse :
. » est fausse :
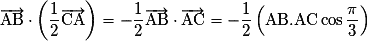 .
.
Soit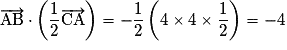 .
.
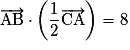 . » est fausse :
. » est fausse :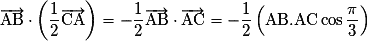 .
.Soit
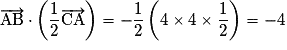 .
.Exercice n°4
Cochez la bonne réponse.
On considère un parallélogramme ABCD tel que AB = 3, BC = 5 et 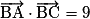 .
.
Laquelle des propositions suivantes est correcte ?
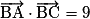 .
.Laquelle des propositions suivantes est correcte ?
Cochez la bonne réponse.
| ||
| ||
|
• 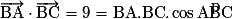 .
.
D'où on déduit que :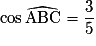 .
.
On applique alors la formule d'Al-Kashi dans le triangle ABC : .
.
En remplaçant par les valeurs numériques, on trouve :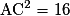 d'où le résultat.
d'où le résultat.
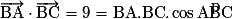 .
.D'où on déduit que :
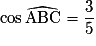 .
.On applique alors la formule d'Al-Kashi dans le triangle ABC :
 .
.En remplaçant par les valeurs numériques, on trouve :
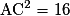 d'où le résultat.
d'où le résultat.• 3,6 n'est pas la valeur exacte de OD mais seulement une valeur approchée, donc on ne peut pas écrire l'égalité.
• 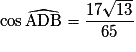 . Il y a une erreur dans le signe dans le choix proposé.
. Il y a une erreur dans le signe dans le choix proposé.
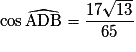 . Il y a une erreur dans le signe dans le choix proposé.
. Il y a une erreur dans le signe dans le choix proposé.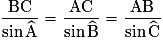 .
.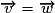 , alors, pour tout vecteur
, alors, pour tout vecteur 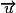 , on a :
, on a : 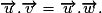
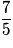
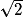
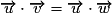 , alors
, alors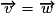 .
.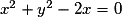 et
et 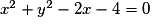 sont concentriques.
sont concentriques.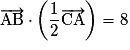 .
.