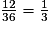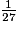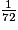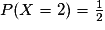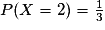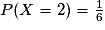Les probabilités conditionnelles prennent en compte les informations concernant l'issue d'une expérience qui modifient la probabilité des événements liés à cette expérience. On parle de probabilités conditionnelles lorsque deux événements d'une expérience aléatoire se réalisent l'un après l'autre, on regarde alors l'influence du premier sur le second.
1. Comment calculer une probabilité conditionnelle ?
Lecture d'un arbre
On considère une expérience aléatoire et deux événements A et B quelconques de probabilités non nulles. L'événement A est réalisé puis l'événement B.On peut visualiser la situation en utilisant un arbre pondéré :
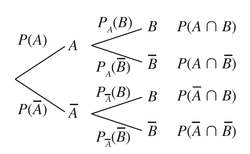 |
La probabilité de l'événement « B sachant que l'événement A est réalisé », notée PA (B) peut se calculer en utilisant un arbre.
En effet on a :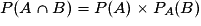 donc
donc 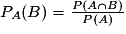 .
.
Par analogie on en déduit que la probabilité de l'événement « A sachant que l'événement B est réalisé », notée PB (A) sera égale à :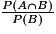 .
.
Exercice n°1
En effet on a :
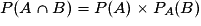 donc
donc 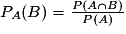 .
.Par analogie on en déduit que la probabilité de l'événement « A sachant que l'événement B est réalisé », notée PB (A) sera égale à :
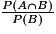 .
.Exercice n°1
2. Comment montrer que deux événements sont indépendants ?
Propriété
Intuitivement, deux événements sont indépendants si la réalisation de l'un de ces événements n'influe pas sur la probabilité de l'autre. On doit donc avoir : PA(B) = P(B).A et B sont donc indépendants si et seulement si
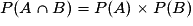 .
.Remarque
Attention à ne pas confondre incompatibles et indépendants :- A et B sont donc incompatibles si et seulement si
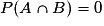 ;
; - A et B sont donc indépendants si et seulement si
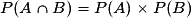 .
.
3. Comment utiliser la formule des probabilités totales ?
4. Comment estimer la valeur de π grâce aux probabilités ?
Algorithme : Approximation de Pi par la méthode de Monte-Carlo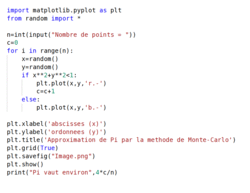 |
En choisissant mille points (n=1000) on obtient par exemple ceci :
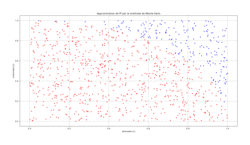 |
À retenir
- La probabilité de l'événement « B sachant que l'événement A est réalisé » (avec
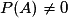 ) est
) est 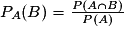 .
. - A et B sont indépendants si et seulement si
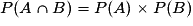 .
. 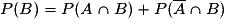 .
.
Exercice n°1
On considère l'arbre pondéré suivant :
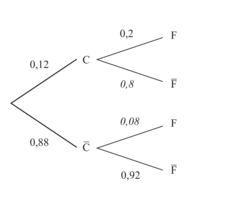 |
À quoi est égale PC (F) ?
Cochez la bonne réponse.
| ||
| ||
|
On cherche la probabilité que l'événement F se réalise sachant que l'événement C s'est déjà réalisé.
0,12 est la valeur de C et 0,2 est la valeur de F
Pour calculer P(F) sachant C on applique P(C)×P(F) sachant C = 0,12 × 0,2 = 0,024
0,12 est la valeur de C et 0,2 est la valeur de F
Pour calculer P(F) sachant C on applique P(C)×P(F) sachant C = 0,12 × 0,2 = 0,024
Exercice n°2
Dans une population lycéenne, 40 % des élèves aiment les mathématiques, 30 % aiment la physique et 10 % aiment à la fois les mathématiques et la physique.
On prend un élève au hasard, la probabilité pour qu'il n'aime pas les mathématiques sachant qu'il aime la physique est égale à :
On prend un élève au hasard, la probabilité pour qu'il n'aime pas les mathématiques sachant qu'il aime la physique est égale à :
Cochez la bonne réponse.
| ||
| ||
|
Soit A l'événement « l'élève aime les mathématiques » et B l'événement « l'élève aime la physique ».
On a P(A) = 0,4 ; P(B) = 0,3 et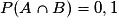 .
.
On cherche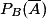 .
.
On sait que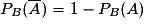 .
.
Or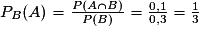 .
.
Donc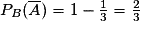 .
.
On a P(A) = 0,4 ; P(B) = 0,3 et
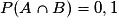 .
.On cherche
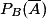 .
.On sait que
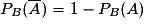 .
.Or
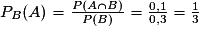 .
.Donc
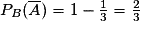 .
.Exercice n°3
On considère deux événements indépendants A et B tels que P(A) = 0,8 et 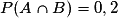 .
.
À quoi est égale :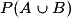 ?
?
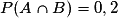 .
.À quoi est égale :
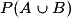 ?
? Cochez la bonne réponse.
| ||
| ||
|
On sait que 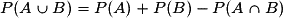 .
.
On sait que A et B sont indépendants donc :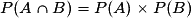 .
.
On en déduit que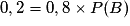 .
.
D'où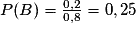 .
.
Donc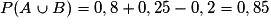 .
.
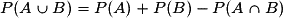 .
.On sait que A et B sont indépendants donc :
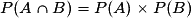 .
.On en déduit que
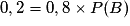 .
.D'où
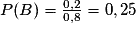 .
.Donc
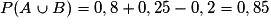 .
.Exercice n°4
On considère une urne contenant 8 jetons rouges, 3 jetons verts et 1 jeton jaune.
On procède à 3 tirages avec remise d'un jeton dans cette urne.
Quelle est la probabilité d'obtenir un jeton rouge, puis un jeton vert et un jeton jaune ?
On procède à 3 tirages avec remise d'un jeton dans cette urne.
Quelle est la probabilité d'obtenir un jeton rouge, puis un jeton vert et un jeton jaune ?
Cochez la bonne réponse.
| ||
| ||
|
Au total l'urne contient 12 jetons.
La probabilité d'obtenir un jeton rouge est égale à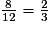 .
.
La probabilité d'obtenir un jeton vert est égale à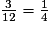 .
.
La probabilité d'obtenir un jeton jaune est égale à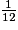 .
.
Puisqu'à chaque tirage on remet le jeton tiré, les événements sont indépendants donc :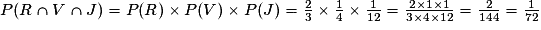 .
.
La probabilité d'obtenir un jeton rouge est égale à
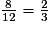 .
.La probabilité d'obtenir un jeton vert est égale à
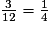 .
.La probabilité d'obtenir un jeton jaune est égale à
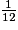 .
.Puisqu'à chaque tirage on remet le jeton tiré, les événements sont indépendants donc :
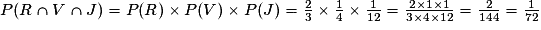 .
.Exercice n°5
On considère une urne contenant 8 jetons rouges, 3 jetons verts et 1 jeton jaune.
On procède à 3 tirages avec remise d'un jeton dans cette urne.
La probabilité d'obtenir un jeton rouge, puis un jeton vert et un jeton jaune est égale à la probabilité d'obtenir un jeton jaune, puis un jeton rouge et un jeton vert.
On procède à 3 tirages avec remise d'un jeton dans cette urne.
La probabilité d'obtenir un jeton rouge, puis un jeton vert et un jeton jaune est égale à la probabilité d'obtenir un jeton jaune, puis un jeton rouge et un jeton vert.
Cochez la bonne réponse.
| ||
|
Puisqu'à chaque tirage on remet le jeton tiré, les événements sont indépendants donc : 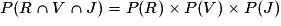 .
.
La multiplication est commutative (l'ordre n'a pas d'importance) donc :
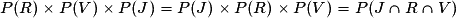 .
.
L'ordre n'a donc pas d'importance, l'affirmation est vraie.
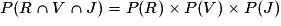 .
.La multiplication est commutative (l'ordre n'a pas d'importance) donc :
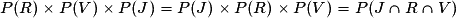 .
.L'ordre n'a donc pas d'importance, l'affirmation est vraie.
Exercice n°6
On tire une carte d'un jeu de 32 cartes. On considère les événements suivants :
C : « La carte est un cœur. »
F : « La carte est une figure (valet, roi ou dame). »
V : « La carte est un valet. »
Quels sont les deux événements dépendants ?
C : « La carte est un cœur. »
F : « La carte est une figure (valet, roi ou dame). »
V : « La carte est un valet. »
Quels sont les deux événements dépendants ?
Cochez la bonne réponse.
| ||
| ||
|
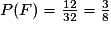 et
et 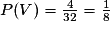 .
.On calcule :
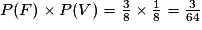 .
.Par ailleurs :
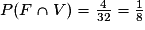 .
.Comme
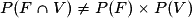 , les événements F et V sont donc dépendants.
, les événements F et V sont donc dépendants.Exercice n°7
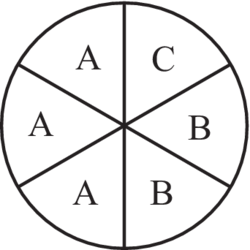
La roue de loterie représentée ci-après est partagée en six secteurs de même angle. Trois sont notés A, deux sont notés B et un est noté C. On fait tourner la roue.
Si elle s'arrête sur un secteur A, le joueur ne gagne rien.
Si elle s'arrête sur un secteur B, il gagne 2 €.
Si elle s'arrête sur un secteur C, il gagne 5 €.
On appelle X la variable aléatoire associée au gain du joueur pour un lancer de roue.
Si elle s'arrête sur un secteur A, le joueur ne gagne rien.
Si elle s'arrête sur un secteur B, il gagne 2 €.
Si elle s'arrête sur un secteur C, il gagne 5 €.
On appelle X la variable aléatoire associée au gain du joueur pour un lancer de roue.
 |
La probabilité d'un gain de 2 euros est donnée par :
Cochez la bonne réponse.
| ||
| ||
|
• Deux secteurs sur six rapportent 2 euros. Donc : 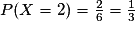 .
.
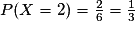 .
.Exercice n°8
La roue de loterie représentée ci-après est partagée en six secteurs de même angle. Trois sont notés A, deux sont notés B et un est noté C. On fait tourner la roue.
Si elle s'arrête sur un secteur A, le joueur ne gagne rien.
Si elle s'arrête sur un secteur B, il gagne 2 €.
Si elle s'arrête sur un secteur C, il gagne 5 €.
On appelle X la variable aléatoire associée au gain du joueur pour un lancer de roue.
Si elle s'arrête sur un secteur A, le joueur ne gagne rien.
Si elle s'arrête sur un secteur B, il gagne 2 €.
Si elle s'arrête sur un secteur C, il gagne 5 €.
On appelle X la variable aléatoire associée au gain du joueur pour un lancer de roue.
 |
L'espérance mathématique de X est donnée par :
Cochez la bonne réponse.
| ||
| ||
|
• La loi de probabilité de X est donnée par le tableau suivant :
D'où :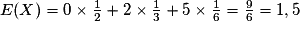 .
.
Pour un grand nombre de jeux, on peut espérer gagner en moyenne 1,5 €.
| xi | 0 | 2 | 5 | Total |
| P(X = xi) | 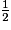 | 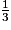 | 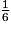 | 1 |
D'où :
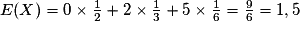 .
.Pour un grand nombre de jeux, on peut espérer gagner en moyenne 1,5 €.
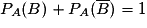 .
.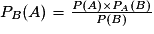 .
. et
et  .
.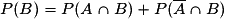 .
.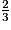 .
.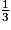 .
.