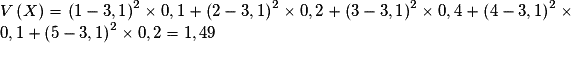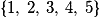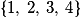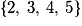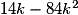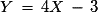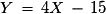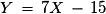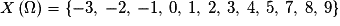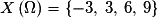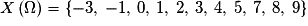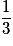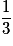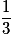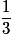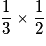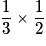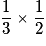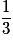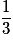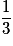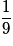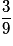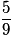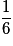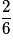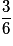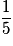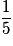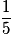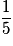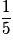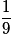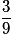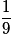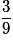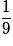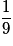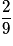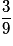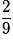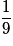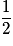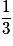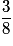Nous allons définir ici des fonctions sur les événements élémentaires, ce qu'on appelle des variables aléatoires. On définit pour ces variables aléatoires leur loi de probabilité et on leur associe un nombre appelé espérance mathématique, qui est à une variable aléatoire ce qu'est la moyenne pour des variables statistiques.
1. Comment reconnaître une variable aléatoire ?
On considère E une expérience aléatoire et Ω l'univers associé.Une variable aléatoire X est simplement une application qui à tout événement élémentaire de l'univers associe un nombre réel.
Autrement dit, X est une fonction :
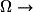
 .
.Remarques
• L'ensemble des valeurs prises par X est noté 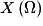 .
.
On se limite dans ce chapitre au cas où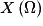 est un ensemble fini de nombres. C'est-à-dire au cas où
est un ensemble fini de nombres. C'est-à-dire au cas où 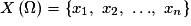 .
.
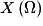 .
.On se limite dans ce chapitre au cas où
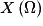 est un ensemble fini de nombres. C'est-à-dire au cas où
est un ensemble fini de nombres. C'est-à-dire au cas où 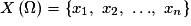 .
.• Une expérience aléatoire dont les issues sont des nombres peut être vue comme une variable aléatoire, dans ce cas : 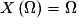 .
.
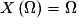 .
.Exemples
• On jette un dé, l'ensemble des issues possibles est {1, 2, 3, 4, 5, 6}. On peut considérer la variable aléatoire X qui, au jet du dé, associe le nombre obtenu. On a 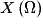 = Ω(voir la remarque précédente).
= Ω(voir la remarque précédente).
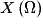 = Ω(voir la remarque précédente).
= Ω(voir la remarque précédente).• On jette deux dés : un dé rouge et un dé blanc. Ω, l'univers associé à cette expérience, est l'ensemble des couples formés par le résultat du dé rouge et le résultat du dé blanc. Par exemple : (2 ; 3) signifie que l'on a obtenu 2 avec le dé rouge et 3 avec le dé blanc.
Le nombre d'éléments de Ωest 36. On considère la variable aléatoire X définie comme la somme des points obtenus, c'est la variable aléatoire qui, au résultat (2 ; 3), associe le nombre 5. On a alors :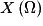 = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
= {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
Exercice n°1Exercice n°2
Le nombre d'éléments de Ωest 36. On considère la variable aléatoire X définie comme la somme des points obtenus, c'est la variable aléatoire qui, au résultat (2 ; 3), associe le nombre 5. On a alors :
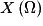 = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
= {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.Exercice n°1Exercice n°2
2. Comment établir la loi de probabilité d'une variable aléatoire ?
• Soit X une variable aléatoire, dont l'ensemble des valeurs prises est 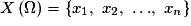 .
.
La loi de probabilité de X est simplement la donnée, pour chaque xi, de la probabilité pi de l'événement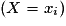 constitué de tous les événements élémentaires dont l'image par X est xi.
constitué de tous les événements élémentaires dont l'image par X est xi.
On la présente généralement sous la forme d'un tableau :
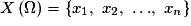 .
.La loi de probabilité de X est simplement la donnée, pour chaque xi, de la probabilité pi de l'événement
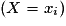 constitué de tous les événements élémentaires dont l'image par X est xi.
constitué de tous les événements élémentaires dont l'image par X est xi.On la présente généralement sous la forme d'un tableau :
| X | x1 | x2 | … | xn | |
| P | p1 | p2 | … | pn | 1 |
Les nombres pi vérifient les conditions :
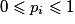 avec
avec 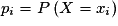 et
et 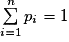 .
.• Dans la pratique, on suit plus ou moins cette démarche. On regarde d'abord l'image d'événements élémentaires, puis on détermine 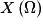 . Enfin, pour chaque xi, on calcule la probabilité pi de l'événement
. Enfin, pour chaque xi, on calcule la probabilité pi de l'événement 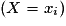 .
.
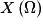 . Enfin, pour chaque xi, on calcule la probabilité pi de l'événement
. Enfin, pour chaque xi, on calcule la probabilité pi de l'événement 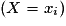 .
.Exemples
On jette une pièce deux fois de suite. C'est l'expérience aléatoire. L'univers associé est 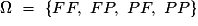 , où FP signifie face au premier lancer et pile au deuxième.
, où FP signifie face au premier lancer et pile au deuxième.
Soit X la variable aléatoire qui, à chaque événement élémentaire, associe le nombre de « face » obtenues. (Donc X associe à FF le nombre 2, à FP le nombre 1, etc.) Les valeurs prises par X sont 0, 1 et 2. La loi de probabilité de X est :
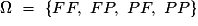 , où FP signifie face au premier lancer et pile au deuxième.
, où FP signifie face au premier lancer et pile au deuxième.Soit X la variable aléatoire qui, à chaque événement élémentaire, associe le nombre de « face » obtenues. (Donc X associe à FF le nombre 2, à FP le nombre 1, etc.) Les valeurs prises par X sont 0, 1 et 2. La loi de probabilité de X est :
| X | 0 | 1 | 2 | |
| P | 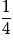 | 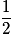 | 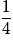 | 1 |
Par exemple P(X = 1) est la probabilité des événements élémentaires dont le nombre de « face » est 1, c'est la probabilité des événements FP et PF.
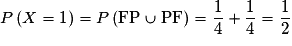 .
.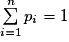 se traduit ici par :
se traduit ici par : 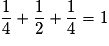 .
.Exercice n°3Exercice n°4Exercice n°5Exercice n°6
3. Comment calculer l'espérance d'une variable aléatoire ?
Soit X une variable aléatoire dont la loi est donnée par 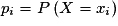 , pour
, pour 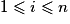 .
.
Autrement dit, la loi de X est :
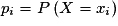 , pour
, pour 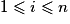 .
.Autrement dit, la loi de X est :
| X | x1 | x2 | … | xn | |
| P | p1 | p2 | … | pn | 1 |
L'espérance de X est le nombre réel noté E( X ) qui est défini par :
 .
.
 .
.Remarques
• L'espérance est la « moyenne » des valeurs prises par X lors d'un grand nombre de répétitions de l'expérience. En effet, si on répète l'expérience et qu'à chaque fois on note la valeur obtenue, la moyenne de ces valeurs tend vers E(X) quand le nombre de répétitions tend vers l'infini.
• L'espérance est comprise entre la plus petite et la plus grande valeur de X.
• Si l'on ajoute la valeur k à toutes les valeurs de X, on ajoute k à E(X). Si l'on multiplie par k toutes les valeurs de X, on multiplie E(X) par k.
Exercice n°7Exercice n°8
Exercice n°7Exercice n°8
4. Comment calculer la variance d'une variable aléatoire ?
Soit X une variable aléatoire dont la loi est donnée par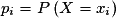 , pour
, pour 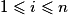 .
.Autrement dit, la loi de X est :
| X | x 1 | x 2 | … | xn | |
| P | p 1 | p 2 | … | pn | 1 |
La variance de X est le nombre réel, noté V( X ), défini par :
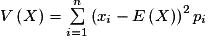 , soit
, soit
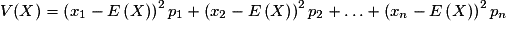
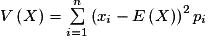 , soit
, soit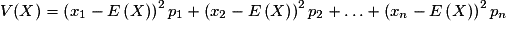
L'écart type de X est le nombre réel, noté 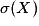 , défini par :
, défini par : 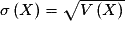 .
.
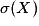 , défini par :
, défini par : 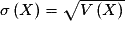 .
.Remarques
• La variance mesure la dispersion de la loi de probabilité autour de l'espérance. On démontre que la probabilité d'obtenir une valeur de X comprise entre E(X) - V(X) et E(X) + V(X) est supérieure à 75 %.
La variance est toujours une valeur positive ou nulle.
La variance est toujours une valeur positive ou nulle.
• Si l'on ajoute la valeur k à toutes les valeurs de X, on ne change pas V(X). Si l'on multiplie par k toutes les valeurs de X on multiplie V(X) par k 2.
• On peut utiliser, pour calculer la variance, la formule suivante :
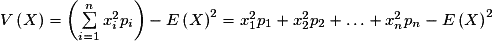 .
.
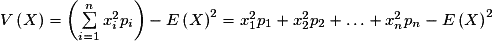 .
.Exemple
Soit la variable aléatoire X de loi :5. Que deviennent l'espérance et la variance par changement de variable aléatoire 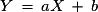 ?
?
Exemple : L'organisateur d'une tombola édite dix mille billets. Dix gagnent un lot à 1 000 €, cent gagnent un lot à 100 €. On achète un billet au hasard et on appelle X la variable aléatoire égale au montant du lot.
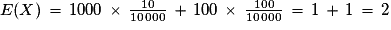 ;
;
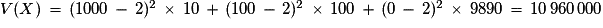
Un billet coûte 3 € et 5 % sont prélevés sur le montant du lot pour une organisation caritative. Si Y est la variable égale au gain alors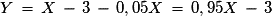 .
.
Soit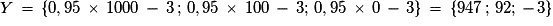
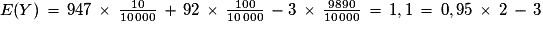 ;
;
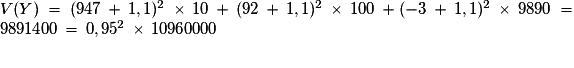 .
.
Plus généralement : Pour a et b réels :
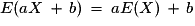 et
et 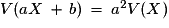 .
.
D'où l'égalité sur les écarts-types :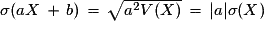 .
.
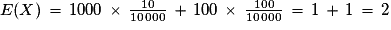 ;
;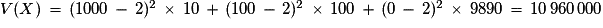
Un billet coûte 3 € et 5 % sont prélevés sur le montant du lot pour une organisation caritative. Si Y est la variable égale au gain alors
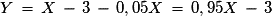 .
.Soit
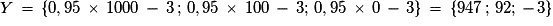
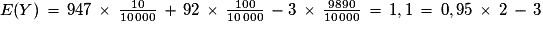 ;
;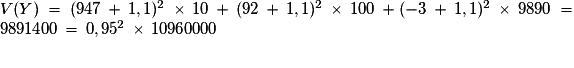 .
.Plus généralement : Pour a et b réels :
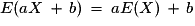 et
et 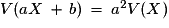 .
.D'où l'égalité sur les écarts-types :
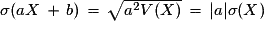 .
.6. Quels sont les algorithmes à maîtriser ?
Calculer l'espérance mathématique d'une variable aléatoire discrète :Soit X une variable aléatoire discréte qui prend pour valeurs x1, x2… xn. On note pi la probabilité de l'événement {X = xi}. On note E(X) l'espérance mathématique de X et σ(X) l'écart-type de X.
 |
L'utilisateur devra entrer les valeurs sous la forme d'une liste de telle manière [x1, x2 … xn]. De même pour les probabilités [p1, p2 … pn].
Calculer l'écart-type d'une variable aléatoire discrète :
Calculer l'écart-type d'une variable aléatoire discrète :
 |
Comment simuler une variable aléatoire discrète à l'aide du module random ?
 |
Comment simuler un échantillon de taille n d'une variable aléatoire discrète ?
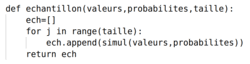 |
Comment analyser un échantillon de taille n d'une variable aléatoire discrète ?
On peut par exemple calculer la moyenne des réels constituants l'échantillon
On peut par exemple calculer la moyenne des réels constituants l'échantillon
 |
On peut aussi mesurer la distance entre E(X) et la moyenne observée dans l'échantillon
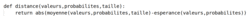 |
Enfin on peut calculer si on simule N échantillons de taille n, la proportion des échantillons dans lesquels la distance entre E(X) et la moyenne observée dans l'échantillon est inférieure ou égale à 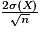 .
.
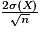 .
. |
À retenir absolument
• Pour déterminer la loi d'une variable aléatoire, on commence par déterminer X ( Ω), puis pour chaque xi, on calcule 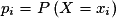 .
.
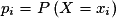 .
.• L'espérance de X est 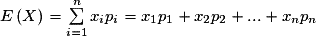 .
.
La variance de X est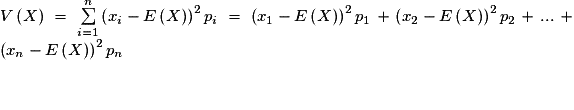 .
.
Pour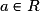 et
et 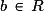 :
: 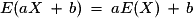 et
et 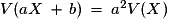 .
.
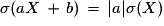 .
.
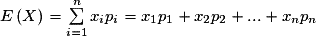 .
.La variance de X est
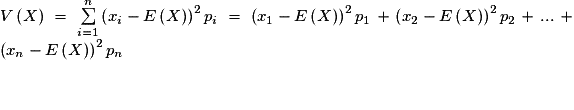 .
.Pour
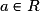 et
et 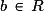 :
: 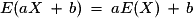 et
et 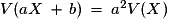 .
.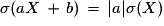 .
.Exercice n°1
Cochez la bonne réponse.
Victor veut des roudoudous. Dans le bocal, il y a 2 roudoudous rouges, 1 roudoudou orange et 3 roudoudous verts. Victor prend les roudoudous un à un dans le bocal. Soit X la variable aléatoire égale au nombre de roudoudous restant dans le bocal quand Victor a épuisé une couleur.
Quel est l'ensemble des valeurs prises par X ?
Cochez la bonne réponse.
| ||
| ||
|
• Le mieux (ou le pire, suivant le point de vue où l'on se place) que Victor puisse faire, c'est d'épuiser une couleur dès le premier tirage, en prenant le roudoudou orange. Il reste alors dans le bocal 5 roudoudous.
• Le pire que Victor puisse faire, c'est d'aller jusqu'à laisser un représentant par couleur puis de refaire un tirage. C'est-à-dire, par exemple, prendre un rouge, puis un vert, puis un vert ; le tirage suivant, quoiqu'il prenne, il épuise une couleur et il reste 2 couleurs dans le bocal, d'où X = 2.
• Au total 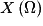 est formé de tous les entiers compris entre 2 et 5 ;
est formé de tous les entiers compris entre 2 et 5 ; 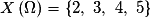 .
.
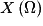 est formé de tous les entiers compris entre 2 et 5 ;
est formé de tous les entiers compris entre 2 et 5 ; 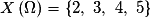 .
.Exercice n°2
Cochez la bonne réponse.
On a la loi suivante :
| Valeur de X | 1 | 2 | 3 |
| Probabilité | k | 2k | 3k |
Quelle est la variance de X ?
Cochez la bonne réponse.
| ||
| ||
|
Calculons d'abord k. On doit avoir k + 2k + 3k = 1. D'où 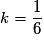 .
.
Alors :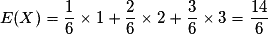 .
.
D'où :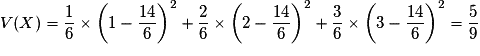 .
.
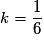 .
.Alors :
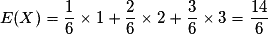 .
.D'où :
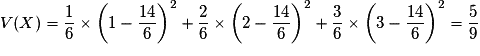 .
.Exercice n°3
Un QCM comporte cinq questions avec deux réponses chacune. Une seule est exacte.
On répond au hasard et X est la variable aléatoire égale au nombre de réponses exactes.
Une bonne réponse rapporte 4 points et une mauvaise coûte 3 points.
Si Y est la variable aléatoire égale au nombre total de points obtenus, quelle fonction affine relie Y à X ?
On répond au hasard et X est la variable aléatoire égale au nombre de réponses exactes.
Une bonne réponse rapporte 4 points et une mauvaise coûte 3 points.
Si Y est la variable aléatoire égale au nombre total de points obtenus, quelle fonction affine relie Y à X ?
Cochez la bonne réponse.
| ||
| ||
|
Si X est le nombre de réponses exactes,  est le nombre de réponses fausses.
est le nombre de réponses fausses.
Donc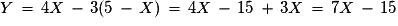 .
.
 est le nombre de réponses fausses.
est le nombre de réponses fausses.Donc
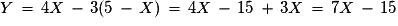 .
.Exercice n°4
On lance un dé cubique équilibré sur un plan de travail. Soit Z la variable aléatoire qui à un lancer de dé associe le résultat obtenu.
Afin de simuler la variable aléatoire Z à l'aide d'un algorithme on devra considérer :
Afin de simuler la variable aléatoire Z à l'aide d'un algorithme on devra considérer :
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
Exercice n°5
La fonction append sert à :
Cochez la bonne réponse.
| ||
| ||
| ||
|
Exercice n°6
Cochez la bonne réponse.
Dans un jeu de 32 cartes, on attribue des valeurs aux cartes selon les modalités suivantes : 3 points aux rois, 2 points aux dames, 1 point aux valets et -1 point aux autres cartes.
On tire 3 cartes au hasard, on appelle X la variable aléatoire : somme des points obtenus.
Quel est l'ensemble des valeurs prises par X ?
Quel est l'ensemble des valeurs prises par X ?
Cochez la bonne réponse.
| ||
| ||
|
La somme des points obtenus est un entier compris entre -3 et 9. Montrons que tous ces entiers sont des valeurs prises par X :
X = -3 si on tire trois « sept » par exemple ;
X = -2 est impossible ;
X = -1 si l'on tire deux « sept » et un valet par exemple ;
X = 0 si l'on tire deux « sept » et une dame par exemple ;
X = 1 si l'on tire un « sept » et deux valets par exemple ;
X = 2 si l'on tire un « sept », un valet et une dame par exemple ;
X = 3 si l'on tire trois valets par exemple ;
X = 4 si l'on tire deux valets et une dame par exemple ;
X = 5 si l'on tire un valet et deux dames par exemple ;
X = 6 si l'on tire trois dames par exemple ;
X = 7 si l'on tire un valet et deux rois par exemple ;
X = 8 si l'on tire une dame et deux rois par exemple ;
X = 9 si l'on tire trois rois.
X = -3 si on tire trois « sept » par exemple ;
X = -2 est impossible ;
X = -1 si l'on tire deux « sept » et un valet par exemple ;
X = 0 si l'on tire deux « sept » et une dame par exemple ;
X = 1 si l'on tire un « sept » et deux valets par exemple ;
X = 2 si l'on tire un « sept », un valet et une dame par exemple ;
X = 3 si l'on tire trois valets par exemple ;
X = 4 si l'on tire deux valets et une dame par exemple ;
X = 5 si l'on tire un valet et deux dames par exemple ;
X = 6 si l'on tire trois dames par exemple ;
X = 7 si l'on tire un valet et deux rois par exemple ;
X = 8 si l'on tire une dame et deux rois par exemple ;
X = 9 si l'on tire trois rois.
Exercice n°7
Cochez la bonne réponse.
Dans le porte-monnaie de Mamie, il y a trois pièces : une de 1 €, une de 2 € et une de 0,5 €. Pour payer sa baguette de pain, elle prend deux pièces au hasard (déjà avec les nouveaux francs, ce n'était pas facile, alors avec les euros…).
On appelle X la somme qu'elle extrait de son porte-monnaie. La loi de X est :
Cochez la bonne réponse.
| ||||||||||
| ||||||||||
|
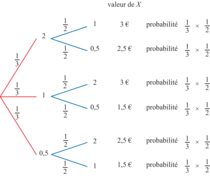 |
On peut faire un arbre en considérant que Mamie prend ses deux pièces l'une après l'autre. On enchaîne deux expériences, d'où l'arbre :
« Obtenir 2,5 € » a donc pour probabilité :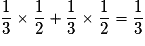 . De même pour les autres valeurs.
. De même pour les autres valeurs.
« Obtenir 2,5 € » a donc pour probabilité :
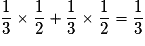 . De même pour les autres valeurs.
. De même pour les autres valeurs.Remarque : on aurait pu raisonner aussi en regardant la pièce restante dans le porte-monnaie. Sortir 2,5 €, c'est laisser la pièce 1 € dans le porte-monnaie. Elles ont toutes la même probabilité de rester, d'où la probabilité 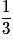 .
.
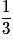 .
.Exercice n°8
Cochez la bonne réponse.
Dans une urne, on place 3 jetons numérotés de 1 à 3. On procède à deux tirages d'un jeton avec remise. On appelle X le plus grand des numéros obtenus.
Quelle est la loi de X ?
Cochez la bonne réponse.
| ||||||||||
| ||||||||||
|
• On peut construire un arbre, mais on peut aussi écrire toutes les issues de l'expérience. L'ensemble des issues possibles est :
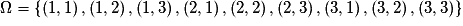 .
.
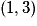 signifie avoir 1 au premier tirage et 3 au deuxième tirage. Toutes ces issues sont équiprobables.
signifie avoir 1 au premier tirage et 3 au deuxième tirage. Toutes ces issues sont équiprobables.
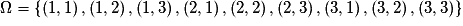 .
.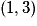 signifie avoir 1 au premier tirage et 3 au deuxième tirage. Toutes ces issues sont équiprobables.
signifie avoir 1 au premier tirage et 3 au deuxième tirage. Toutes ces issues sont équiprobables.• L'événement « le plus grand vaut 1 » est : 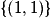 .
.
L'événement « le plus grand vaut 2 » est :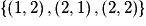 .
.
L'événement « le plus grand vaut 3 » est :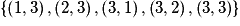 .
.
D'où :
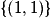 .
.L'événement « le plus grand vaut 2 » est :
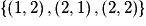 .
.L'événement « le plus grand vaut 3 » est :
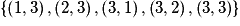 .
.D'où :
| Valeur de X | 1 | 2 | 3 |
| Probabilité | 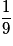 | 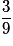 | 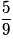 |
Exercice n°9
 |
Cochez la bonne réponse.
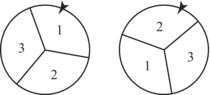
Deux roues sont séparées en trois secteurs égaux numérotés 1, 2 et 3. On fait tourner les deux roues.
Soit X la somme des points obtenus. La loi de X est :
Soit X la somme des points obtenus. La loi de X est :
Cochez la bonne réponse.
| ||||||||||||||
| ||||||||||||||
|
• L'ensemble des valeurs prises par X est 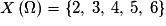 . Ωest l'ensemble des couples (i, j) où i est le numéro donné par la première roue et j, celui donné par la seconde. Il y a ainsi 9 couples possibles, c'est-à-dire 9 issues à notre expérience élémentaire, ces issues sont toutes équiprobables.
. Ωest l'ensemble des couples (i, j) où i est le numéro donné par la première roue et j, celui donné par la seconde. Il y a ainsi 9 couples possibles, c'est-à-dire 9 issues à notre expérience élémentaire, ces issues sont toutes équiprobables.
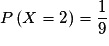 car seul le couple (1, 1) réalise (X = 2).
car seul le couple (1, 1) réalise (X = 2).
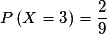 car les couples (2, 1) et (1, 2) réalisent (X = 3).
car les couples (2, 1) et (1, 2) réalisent (X = 3).
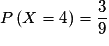 car les couples (3, 1), (2, 2) et (1, 3) réalisent (X = 4).
car les couples (3, 1), (2, 2) et (1, 3) réalisent (X = 4).
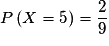 car les couples (2, 3) et (3, 2) réalisent (X = 5).
car les couples (2, 3) et (3, 2) réalisent (X = 5).
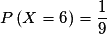 car seul le couple (3, 3) réalise (X = 6).
car seul le couple (3, 3) réalise (X = 6).
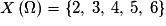 . Ωest l'ensemble des couples (i, j) où i est le numéro donné par la première roue et j, celui donné par la seconde. Il y a ainsi 9 couples possibles, c'est-à-dire 9 issues à notre expérience élémentaire, ces issues sont toutes équiprobables.
. Ωest l'ensemble des couples (i, j) où i est le numéro donné par la première roue et j, celui donné par la seconde. Il y a ainsi 9 couples possibles, c'est-à-dire 9 issues à notre expérience élémentaire, ces issues sont toutes équiprobables.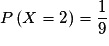 car seul le couple (1, 1) réalise (X = 2).
car seul le couple (1, 1) réalise (X = 2).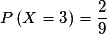 car les couples (2, 1) et (1, 2) réalisent (X = 3).
car les couples (2, 1) et (1, 2) réalisent (X = 3).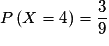 car les couples (3, 1), (2, 2) et (1, 3) réalisent (X = 4).
car les couples (3, 1), (2, 2) et (1, 3) réalisent (X = 4).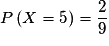 car les couples (2, 3) et (3, 2) réalisent (X = 5).
car les couples (2, 3) et (3, 2) réalisent (X = 5).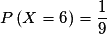 car seul le couple (3, 3) réalise (X = 6).
car seul le couple (3, 3) réalise (X = 6).• D'où la loi :
| Valeur de X | 2 | 3 | 4 | 5 | 6 |
| Probabilité | 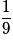 | 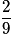 | 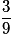 | 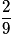 | 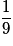 |
•
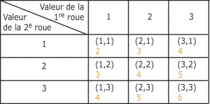 |
Nous aurions pu aussi faire le tableau suivant.
Dans chaque case, on a indiqué le résultat de l'expérience et précisé (en orange) la valeur de X associée. Chaque case a pour probabilité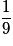 ; il reste à compter, pour chaque valeur de X, le nombre de fois où elle apparaît.
; il reste à compter, pour chaque valeur de X, le nombre de fois où elle apparaît.
Dans chaque case, on a indiqué le résultat de l'expérience et précisé (en orange) la valeur de X associée. Chaque case a pour probabilité
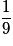 ; il reste à compter, pour chaque valeur de X, le nombre de fois où elle apparaît.
; il reste à compter, pour chaque valeur de X, le nombre de fois où elle apparaît.Exercice n°10
Cochez la bonne réponse.
Anasthase, que les mathématiques anesthésient, hésite pour le programme de sa soirée : soit s'avancer dans ses devoirs, soit aller au cinéma. Pour trancher, il jette trois fois de suite une pièce de 1 euro parfaitement équilibrée et décide que, si le nombre de faces est supérieur ou égal à 2, il s'avancera dans ses devoirs.
Quelle est la probabilité qu'Anasthase s'avance dans ses devoirs ?
Cochez la bonne réponse.
| ||
| ||
|
• Les résultats possibles aux trois lancers sont : PPP ; PPF ; PFP ; PFF ; FPP ; FPF ; FFP ; FFF.
• Soit X le nombre de faces obtenues, la loi de X est définie par :
| Valeur de X | 0 | 1 | 2 | 3 |
| Probabilité | 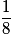 | 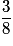 | 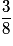 | 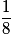 |
La probabilité pour qu'Anasthase s'avance dans ses devoirs est :
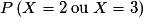 .
.Or
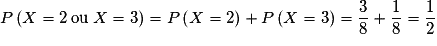 .
.Exercice n°11
Cochez la bonne réponse.
Soit X le nombre d'œufs pondus par semaine par « Idéal du Gravier IV », championne catégorie poids plume de Haute-Picardie. Les valeurs prises par X vont de neuf à la douzaine, avec la loi de probabilité suivante :
| Valeur de X | 9 | 10 | 11 | 12 |
| Probabilité | 0,6 | 0,2 | 0,15 | 0,05 |
Quelle est l'espérance de X ?
Cochez la bonne réponse.
| ||
| ||
|
On calcule l'espérance de X selon la formule : 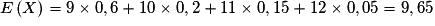 .
.
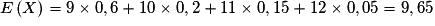 .
.Exercice n°12
Cochez la bonne réponse.
Soit une variable aléatoire X dont la loi de probabilité est donnée par le tableau suivant :
| Valeur de X | 1 | 1 + k | 1 + 2k | 1 + 3k | 1 + 4k |
| Probabilité | 0,1 | 0,3 | 0,3 | 0,2 | 0,1 |
Quelle valeur doit-on donner à k pour que E(X) soit égale à 6,7 ?
Cochez la bonne réponse.
| ||
| ||
|
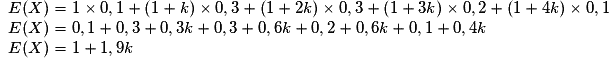
On a donc :
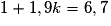 , ce qui est équivalent à
, ce qui est équivalent à 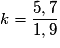 , soit k = 3.
, soit k = 3.Exercice n°13
Cochez la bonne réponse.
Soit X le nombre de devoirs à faire le dimanche où justement il fait beau. La loi de X est donnée par le tableau :
| Valeur de X | 0 | 1 | 2 | 3 | 4 |
| Probabilité | 0,1 | 0,1 | 0,3 | 0,4 | 0,1 |
Quelle est la variance de X ?
Cochez la bonne réponse.
| ||
| ||
|
On calcule d'abord : 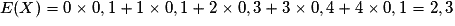 .
.
On a alors :
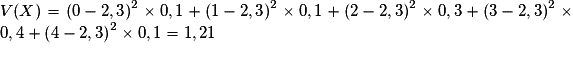 .
.
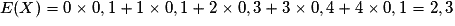 .
.On a alors :
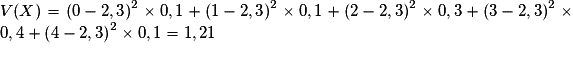 .
.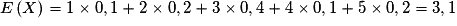 .
.