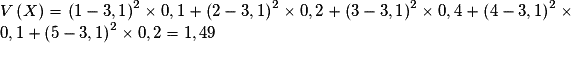Variables aléatoires discrètes
Fiche
Nous allons définir ici des fonctions sur les événements élémentaires, ce qu'on appelle des variables aléatoires. On définit pour ces variables aléatoires leur loi de probabilité et on leur associe un nombre appelé espérance mathématique, qui est à une variable aléatoire ce qu'est la moyenne pour des variables statistiques.
1. Comment reconnaître une variable aléatoire ?
On considère E une expérience aléatoire et Ω l'univers associé.Une variable aléatoire X est simplement une application qui à tout événement élémentaire de l'univers associe un nombre réel.
Autrement dit, X est une fonction :
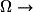
 .
.Remarques
• L'ensemble des valeurs prises par X est noté 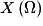 .
.
On se limite dans ce chapitre au cas où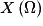 est un ensemble fini de nombres. C'est-à-dire au cas où
est un ensemble fini de nombres. C'est-à-dire au cas où 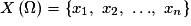 .
.
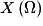 .
.On se limite dans ce chapitre au cas où
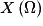 est un ensemble fini de nombres. C'est-à-dire au cas où
est un ensemble fini de nombres. C'est-à-dire au cas où 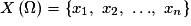 .
.• Une expérience aléatoire dont les issues sont des nombres peut être vue comme une variable aléatoire, dans ce cas : 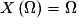 .
.
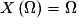 .
.Exemples
• On jette un dé, l'ensemble des issues possibles est {1, 2, 3, 4, 5, 6}. On peut considérer la variable aléatoire X qui, au jet du dé, associe le nombre obtenu. On a 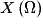 = Ω(voir la remarque précédente).
= Ω(voir la remarque précédente).
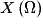 = Ω(voir la remarque précédente).
= Ω(voir la remarque précédente).• On jette deux dés : un dé rouge et un dé blanc. Ω, l'univers associé à cette expérience, est l'ensemble des couples formés par le résultat du dé rouge et le résultat du dé blanc. Par exemple : (2 ; 3) signifie que l'on a obtenu 2 avec le dé rouge et 3 avec le dé blanc.
Le nombre d'éléments de Ωest 36. On considère la variable aléatoire X définie comme la somme des points obtenus, c'est la variable aléatoire qui, au résultat (2 ; 3), associe le nombre 5. On a alors :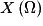 = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
= {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
Exercice n°1Exercice n°2
Le nombre d'éléments de Ωest 36. On considère la variable aléatoire X définie comme la somme des points obtenus, c'est la variable aléatoire qui, au résultat (2 ; 3), associe le nombre 5. On a alors :
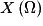 = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
= {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.Exercice n°1Exercice n°2
2. Comment établir la loi de probabilité d'une variable aléatoire ?
• Soit X une variable aléatoire, dont l'ensemble des valeurs prises est 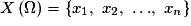 .
.
La loi de probabilité de X est simplement la donnée, pour chaque xi, de la probabilité pi de l'événement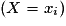 constitué de tous les événements élémentaires dont l'image par X est xi.
constitué de tous les événements élémentaires dont l'image par X est xi.
On la présente généralement sous la forme d'un tableau :
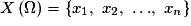 .
.La loi de probabilité de X est simplement la donnée, pour chaque xi, de la probabilité pi de l'événement
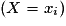 constitué de tous les événements élémentaires dont l'image par X est xi.
constitué de tous les événements élémentaires dont l'image par X est xi.On la présente généralement sous la forme d'un tableau :
| X | x1 | x2 | … | xn | |
| P | p1 | p2 | … | pn | 1 |
Les nombres pi vérifient les conditions :
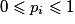 avec
avec 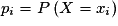 et
et 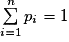 .
.• Dans la pratique, on suit plus ou moins cette démarche. On regarde d'abord l'image d'événements élémentaires, puis on détermine 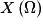 . Enfin, pour chaque xi, on calcule la probabilité pi de l'événement
. Enfin, pour chaque xi, on calcule la probabilité pi de l'événement 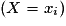 .
.
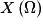 . Enfin, pour chaque xi, on calcule la probabilité pi de l'événement
. Enfin, pour chaque xi, on calcule la probabilité pi de l'événement 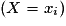 .
.Exemples
On jette une pièce deux fois de suite. C'est l'expérience aléatoire. L'univers associé est 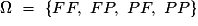 , où FP signifie face au premier lancer et pile au deuxième.
, où FP signifie face au premier lancer et pile au deuxième.
Soit X la variable aléatoire qui, à chaque événement élémentaire, associe le nombre de « face » obtenues. (Donc X associe à FF le nombre 2, à FP le nombre 1, etc.) Les valeurs prises par X sont 0, 1 et 2. La loi de probabilité de X est :
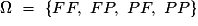 , où FP signifie face au premier lancer et pile au deuxième.
, où FP signifie face au premier lancer et pile au deuxième.Soit X la variable aléatoire qui, à chaque événement élémentaire, associe le nombre de « face » obtenues. (Donc X associe à FF le nombre 2, à FP le nombre 1, etc.) Les valeurs prises par X sont 0, 1 et 2. La loi de probabilité de X est :
| X | 0 | 1 | 2 | |
| P | 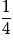 | 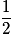 | 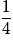 | 1 |
Par exemple P(X = 1) est la probabilité des événements élémentaires dont le nombre de « face » est 1, c'est la probabilité des événements FP et PF.
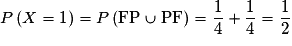 .
. se traduit ici par :
se traduit ici par : 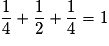 .
.Exercice n°3Exercice n°4Exercice n°5Exercice n°6
3. Comment calculer l'espérance d'une variable aléatoire ?
Soit X une variable aléatoire dont la loi est donnée par 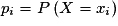 , pour
, pour 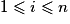 .
.
Autrement dit, la loi de X est :
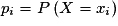 , pour
, pour 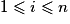 .
.Autrement dit, la loi de X est :
| X | x1 | x2 | … | xn | |
| P | p1 | p2 | … | pn | 1 |
L'espérance de X est le nombre réel noté E( X ) qui est défini par :
 .
.
 .
.Remarques
• L'espérance est la « moyenne » des valeurs prises par X lors d'un grand nombre de répétitions de l'expérience. En effet, si on répète l'expérience et qu'à chaque fois on note la valeur obtenue, la moyenne de ces valeurs tend vers E(X) quand le nombre de répétitions tend vers l'infini.
• L'espérance est comprise entre la plus petite et la plus grande valeur de X.
• Si l'on ajoute la valeur k à toutes les valeurs de X, on ajoute k à E(X). Si l'on multiplie par k toutes les valeurs de X, on multiplie E(X) par k.
Exercice n°7Exercice n°8
Exercice n°7Exercice n°8
4. Comment calculer la variance d'une variable aléatoire ?
Soit X une variable aléatoire dont la loi est donnée par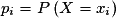 , pour
, pour 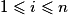 .
.Autrement dit, la loi de X est :
| X | x 1 | x 2 | … | xn | |
| P | p 1 | p 2 | … | pn | 1 |
La variance de X est le nombre réel, noté V( X ), défini par :
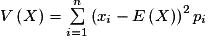 , soit
, soit
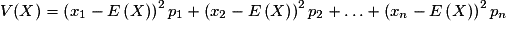
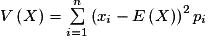 , soit
, soit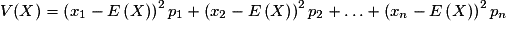
L'écart type de X est le nombre réel, noté 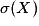 , défini par :
, défini par : 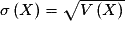 .
.
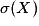 , défini par :
, défini par : 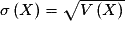 .
.Remarques
• La variance mesure la dispersion de la loi de probabilité autour de l'espérance. On démontre que la probabilité d'obtenir une valeur de X comprise entre E(X) - V(X) et E(X) + V(X) est supérieure à 75 %.
La variance est toujours une valeur positive ou nulle.
La variance est toujours une valeur positive ou nulle.
• Si l'on ajoute la valeur k à toutes les valeurs de X, on ne change pas V(X). Si l'on multiplie par k toutes les valeurs de X on multiplie V(X) par k 2.
• On peut utiliser, pour calculer la variance, la formule suivante :
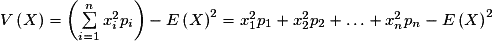 .
.
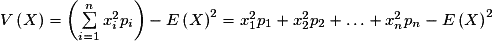 .
.Exemple
Soit la variable aléatoire X de loi :5. Que deviennent l'espérance et la variance par changement de variable aléatoire 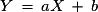 ?
?
Exemple : L'organisateur d'une tombola édite dix mille billets. Dix gagnent un lot à 1 000 €, cent gagnent un lot à 100 €. On achète un billet au hasard et on appelle X la variable aléatoire égale au montant du lot.
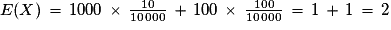 ;
;
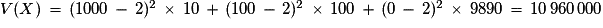
Un billet coûte 3 € et 5 % sont prélevés sur le montant du lot pour une organisation caritative. Si Y est la variable égale au gain alors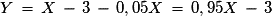 .
.
Soit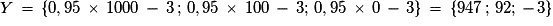
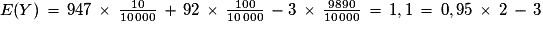 ;
;
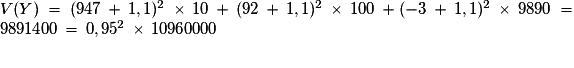 .
.
Plus généralement : Pour a et b réels :
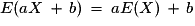 et
et 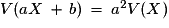 .
.
D'où l'égalité sur les écarts-types :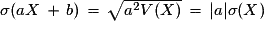 .
.
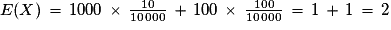 ;
;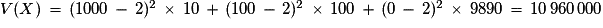
Un billet coûte 3 € et 5 % sont prélevés sur le montant du lot pour une organisation caritative. Si Y est la variable égale au gain alors
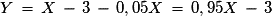 .
.Soit
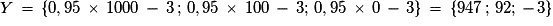
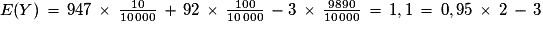 ;
;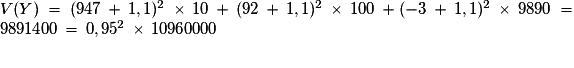 .
.Plus généralement : Pour a et b réels :
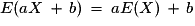 et
et 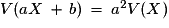 .
.D'où l'égalité sur les écarts-types :
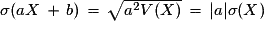 .
.6. Quels sont les algorithmes à maîtriser ?
Calculer l'espérance mathématique d'une variable aléatoire discrète :Soit X une variable aléatoire discréte qui prend pour valeurs x1, x2… xn. On note pi la probabilité de l'événement {X = xi}. On note E(X) l'espérance mathématique de X et σ(X) l'écart-type de X.
 |
L'utilisateur devra entrer les valeurs sous la forme d'une liste de telle manière [x1, x2 … xn]. De même pour les probabilités [p1, p2 … pn].
Calculer l'écart-type d'une variable aléatoire discrète :
Calculer l'écart-type d'une variable aléatoire discrète :
 |
Comment simuler une variable aléatoire discrète à l'aide du module random ?
 |
Comment simuler un échantillon de taille n d'une variable aléatoire discrète ?
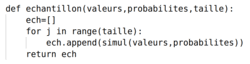 |
Comment analyser un échantillon de taille n d'une variable aléatoire discrète ?
On peut par exemple calculer la moyenne des réels constituants l'échantillon
On peut par exemple calculer la moyenne des réels constituants l'échantillon
 |
On peut aussi mesurer la distance entre E(X) et la moyenne observée dans l'échantillon
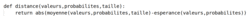 |
Enfin on peut calculer si on simule N échantillons de taille n, la proportion des échantillons dans lesquels la distance entre E(X) et la moyenne observée dans l'échantillon est inférieure ou égale à 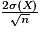 .
.
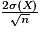 .
. |
À retenir absolument
• Pour déterminer la loi d'une variable aléatoire, on commence par déterminer X ( Ω), puis pour chaque xi, on calcule 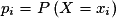 .
.
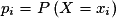 .
.• L'espérance de X est 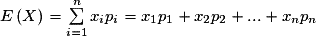 .
.
La variance de X est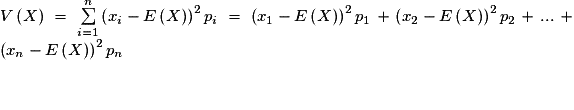 .
.
Pour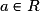 et
et 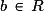 :
: 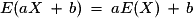 et
et 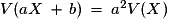 .
.
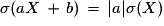 .
.
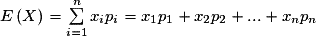 .
.La variance de X est
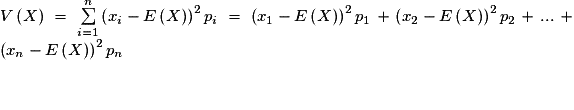 .
.Pour
 et
et 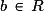 :
: 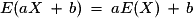 et
et 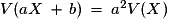 .
.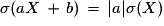 .
.© 2000-2025, Miscellane
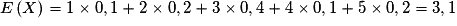 .
.