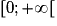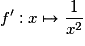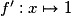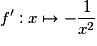Le concept de dérivée n'a été dégagé qu'il y a environ trois siècles. Il est lié, en mathématiques, à la notion de tangente à une courbe, et en sciences physiques, à celle de vitesse instantanée d'un mobile. Les calculs de dérivées ont de nombreuses applications : ils permettent de déterminer les variations d'une fonction, de résoudre des problèmes d'optimisation, de calculer certaines limites, etc.
1. Comment définir le nombre dérivé d'une fonction en un réel ?
Soit f une fonction définie sur un intervalle I ouvert et a un réel appartenant à I.
On dit que f est dérivable en a si le taux d'accroissement de f en a admet une limite finie quand x tend vers a. Dans ce cas, ce réel est appelé le nombre dérivé de f en a et est noté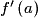 :
:
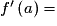
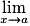
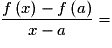
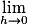
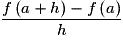 .
.
Exercice n°1
On dit que f est dérivable en a si le taux d'accroissement de f en a admet une limite finie quand x tend vers a. Dans ce cas, ce réel est appelé le nombre dérivé de f en a et est noté
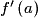 :
: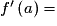
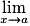
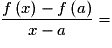
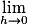
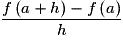 .
.Exercice n°1
2. Que représente le nombre dérivé d'une fonction en un réel ?
Lorsqu'une fonction f est dérivable en un réel a d'un intervalle ouvert I, le nombre dérivé de f en a, 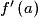 , est le coefficient directeur de la tangente à C, la courbe représentative de f, au point d'abscisse a de C.
, est le coefficient directeur de la tangente à C, la courbe représentative de f, au point d'abscisse a de C.
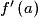 , est le coefficient directeur de la tangente à C, la courbe représentative de f, au point d'abscisse a de C.
, est le coefficient directeur de la tangente à C, la courbe représentative de f, au point d'abscisse a de C.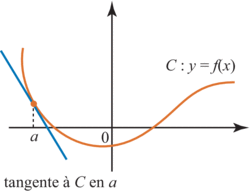 |
3. Quelle est l'équation de la tangente à la courbe d'une fonction, en un point ?
Soit f une fonction définie sur un intervalle ouvert I, dérivable en un réel a de I. On note T la tangente à la courbe représentative de f au point d'abscisse a.
Par définition, T est une droite de coefficient directeur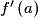 . De plus, T passe par le point
. De plus, T passe par le point 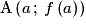 .
.
En traduisant ces deux conditions, on obtient l'équation de T :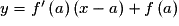 .
.
Exercice n°4
Par définition, T est une droite de coefficient directeur
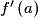 . De plus, T passe par le point
. De plus, T passe par le point 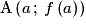 .
.En traduisant ces deux conditions, on obtient l'équation de T :
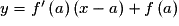 .
.Exercice n°4
4. Existe-t-il des fonctions non dérivables en a ?
Exemple 1 :Étudions la dérivabilité de la fonction racine carrée en 0.
On considère la fonction f définie sur
 + par
+ par 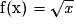 .
.Pour cela, on étudie la limite du taux d'accroissement de f entre 0 et 0 + h :
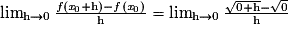
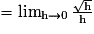
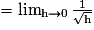

La limite n'est pas un nombre réel fini. La fonction racine carrée n'est donc pas dérivable en 0. Cependant, la courbe admet, au point d'abscisse 0, une demi-tangente verticale.
Exemple 2 :
Étudions la dérivabilité de la fonction valeur absolue en 0.
On considère la fonction f définie sur
 par f(x) = | x |.
par f(x) = | x |.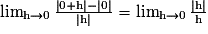
Or, la quantité
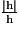 n'a pas de limite en 0. En effet :
n'a pas de limite en 0. En effet :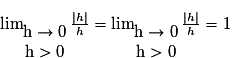 et
et 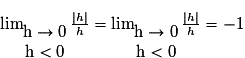
(Les limites à gauche et à droite sont différentes…)
Le taux d'accroissement de la fonction f entre 0 et 0 + h n'a pas de limite en 0. Par conséquent la fonction valeur absolue n'est pas dérivable en 0.
Cependant, elle est dérivable "à droite" de 0 et "à gauche" de 0.
La courbe admet donc deux demi-tangentes distinctes de coefficients directeurs respectifs 1 et −1
Exercice n°5
5. Qu'est-ce que la fonction dérivée d'une fonction dérivable sur un intervalle ?
• Soit f une fonction définie sur un intervalle ouvert I.
On dit que f est dérivable sur I lorsque f est dérivable en tout réel x de I.
On dit que f est dérivable sur I lorsque f est dérivable en tout réel x de I.
• Soit f une fonction définie et dérivable sur un intervalle I.
La fonction qui, à tout réel x de I, associe le nombre dérivé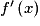 est appelée la fonction dérivée de f sur I. Elle est notée f'.
est appelée la fonction dérivée de f sur I. Elle est notée f'.
Exercice n°6Exercice n°7
La fonction qui, à tout réel x de I, associe le nombre dérivé
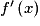 est appelée la fonction dérivée de f sur I. Elle est notée f'.
est appelée la fonction dérivée de f sur I. Elle est notée f'.Exercice n°6Exercice n°7
À retenir
• Une fonction f, définie sur un intervalle ouvert contenant un réel a, est dérivable en a si 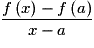 admet une limite finie lorsque x tend vers a. Ce réel est alors noté
admet une limite finie lorsque x tend vers a. Ce réel est alors noté 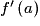 et appelé le « nombre dérivé de f en a ».
et appelé le « nombre dérivé de f en a ».
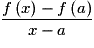 admet une limite finie lorsque x tend vers a. Ce réel est alors noté
admet une limite finie lorsque x tend vers a. Ce réel est alors noté 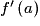 et appelé le « nombre dérivé de f en a ».
et appelé le « nombre dérivé de f en a ».• Dans ce cas, 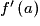 est le coefficient directeur de la tangente à la courbe représentative de f au point d'abscisse a. Cette tangente a alors pour équation
est le coefficient directeur de la tangente à la courbe représentative de f au point d'abscisse a. Cette tangente a alors pour équation 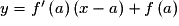 .
.
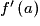 est le coefficient directeur de la tangente à la courbe représentative de f au point d'abscisse a. Cette tangente a alors pour équation
est le coefficient directeur de la tangente à la courbe représentative de f au point d'abscisse a. Cette tangente a alors pour équation 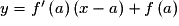 .
.• Si une fonction f est définie et dérivable en tout réel x d'un intervalle ouvert I, alors la fonction qui, à tout 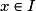 , associe
, associe 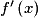 est la fonction dérivée de f sur I, elle est notée f'.
est la fonction dérivée de f sur I, elle est notée f'.
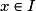 , associe
, associe 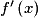 est la fonction dérivée de f sur I, elle est notée f'.
est la fonction dérivée de f sur I, elle est notée f'.Exercice n°1
Cochez la bonne réponse.
Quel est le nombre dérivé en 4 de la fonction f définie sur  par :
par : 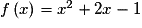 ?
?
 par :
par : 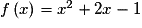 ?
? Cochez la bonne réponse.
| ||
| ||
|
Pour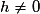 , on a :
, on a :
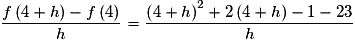
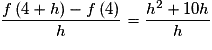
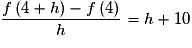
Or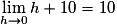 , donc le nombre dérivé de f en 4 existe et vaut
, donc le nombre dérivé de f en 4 existe et vaut 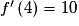 .
.
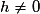 , on a :
, on a :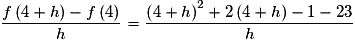
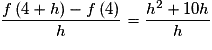
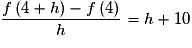
Or
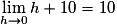 , donc le nombre dérivé de f en 4 existe et vaut
, donc le nombre dérivé de f en 4 existe et vaut 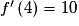 .
.Exercice n°2
Cochez la bonne réponse.
On a représenté ci-dessous la courbe d'une fonction f définie et dérivable sur l'intervalle ![\left] { - 3 \, ; \: 5} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_08_m34.png) :
:
![\left] { - 3 \, ; \: 5} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_08_m34.png) :
: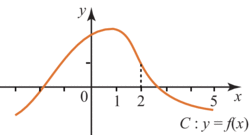 |
Le nombre dérivé de f en 2 est :
Cochez la bonne réponse.
| ||
| ||
|
Le nombre f'(2) est le coefficient directeur de la tangente à la courbe représentative de f au point d'abscisse 2 de cette courbe.
Sur le dessin, la fonction f est clairement strictement décroissante au point d'abscisse 2, donc f'(2) est strictement négatif.
Sur le dessin, la fonction f est clairement strictement décroissante au point d'abscisse 2, donc f'(2) est strictement négatif.
Exercice n°3
Cochez la bonne réponse.
Soit g la fonction définie sur  par
par 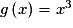 . En quels points la courbe de g admet-elle une tangente parallèle à la droite D d'équation :
. En quels points la courbe de g admet-elle une tangente parallèle à la droite D d'équation : 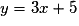 ?
?
 par
par 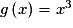 . En quels points la courbe de g admet-elle une tangente parallèle à la droite D d'équation :
. En quels points la courbe de g admet-elle une tangente parallèle à la droite D d'équation : 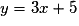 ?
? Cochez la bonne réponse.
| ||
| ||
|
• Soit a un réel quelconque.
Pour , on a :
, on a :
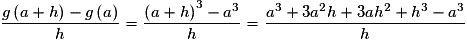 , soit
, soit
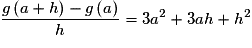 .
.
Or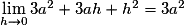 , qui est un réel fini.
, qui est un réel fini.
Donc g est dérivable en tout réel a, d'où g est dérivable sur et, pour tout
et, pour tout 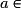
 ,
, 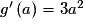 .
.
Pour
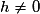 , on a :
, on a :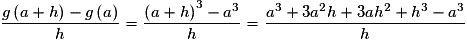 , soit
, soit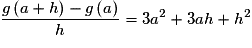 .
.Or
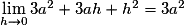 , qui est un réel fini.
, qui est un réel fini.Donc g est dérivable en tout réel a, d'où g est dérivable sur
 et, pour tout
et, pour tout 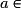
 ,
, 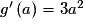 .
.• On cherche pour quels réels a le coefficient directeur de la tangente à la courbe de g au point d'abscisse a est égal à celui de la droite d'équation 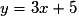 , c'est-à-dire égal à 3.
, c'est-à-dire égal à 3.
On résout donc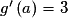 , soit
, soit 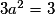 , ou encore
, ou encore 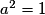 . Les solutions sont :
. Les solutions sont : 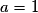 ou
ou 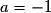 .
.
Ainsi, les points cherchés sont :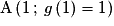 et
et 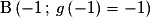 .
.
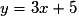 , c'est-à-dire égal à 3.
, c'est-à-dire égal à 3.On résout donc
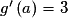 , soit
, soit 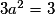 , ou encore
, ou encore 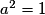 . Les solutions sont :
. Les solutions sont : 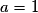 ou
ou 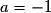 .
.Ainsi, les points cherchés sont :
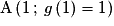 et
et 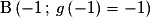 .
.Exercice n°4
Cochez la bonne réponse.
Soit g la fonction définie sur  par
par 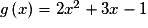 .
.
Une équation de la tangente T à la courbe de g au point d'abscisse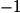 est :
est :
 par
par 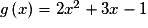 .
.Une équation de la tangente T à la courbe de g au point d'abscisse
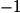 est :
est : Cochez la bonne réponse.
| ||
| ||
|
Pour 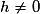 , on a :
, on a :
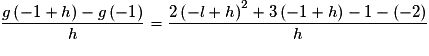
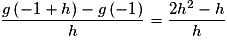
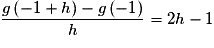
Or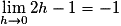 donc g est dérivable en
donc g est dérivable en 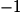 et
et 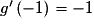 .
.
Donc T a pour équation :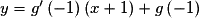 ,
,
soit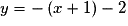 , ou encore
, ou encore 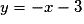 .
.
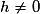 , on a :
, on a :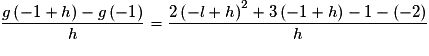
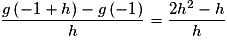
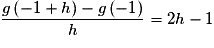
Or
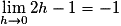 donc g est dérivable en
donc g est dérivable en 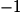 et
et 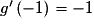 .
.Donc T a pour équation :
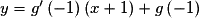 ,
,soit
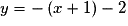 , ou encore
, ou encore 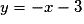 .
.Exercice n°5
Soit g la fonction définie pour tout x de [0;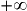 [ par
[ par 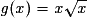 .
.
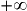 [ par
[ par 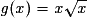 .
.Le taux d'accroissement de g entre 0 et 0+h est égal à :
Cochez la bonne réponse.
| ||
| ||
| ||
|
Exercice n°6
Cochez la bonne réponse.
Soit la fonction g définie sur  par
par 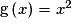 .
.
 par
par 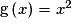 .
. Cochez la bonne réponse.
| ||
| ||
|
• Soit a un réel quelconque de  .
.
Pour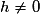 ,
,
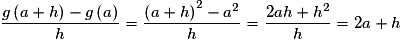 .
.
Or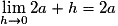 qui est un réel fini.
qui est un réel fini.
Donc f est dérivable en tout réel a de .
.
D'où f est dérivable sur .
.
 .
.Pour
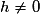 ,
,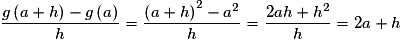 .
.Or
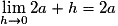 qui est un réel fini.
qui est un réel fini.Donc f est dérivable en tout réel a de
 .
.D'où f est dérivable sur
 .
.Exercice n°7
Cochez la bonne réponse.
Soit la fonction 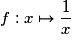 ; elle est dérivable sur
; elle est dérivable sur 
 . Quelle est sa fonction dérivée ?
. Quelle est sa fonction dérivée ?
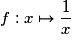 ; elle est dérivable sur
; elle est dérivable sur 
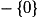 . Quelle est sa fonction dérivée ?
. Quelle est sa fonction dérivée ? Cochez la bonne réponse.
| ||
| ||
|
Soit a un réel quelconque de 
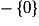 .
.
Pour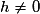 ,
,
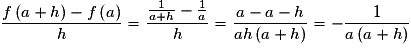
Or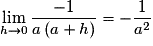 qui est un réel fini.
qui est un réel fini.
Donc f est bien dérivable sur
 et, pour tout
et, pour tout  ,
, 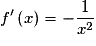 .
.

 .
.Pour
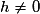 ,
,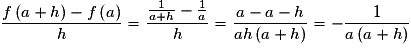
Or
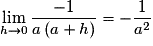 qui est un réel fini.
qui est un réel fini.Donc f est bien dérivable sur

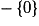 et, pour tout
et, pour tout 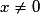 ,
, 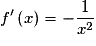 .
.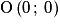
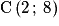 et
et 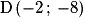
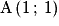 et
et 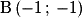
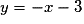
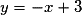
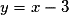
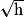 et donc g est dérivable en 0.
et donc g est dérivable en 0.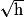 et donc g n'est pas dérivable en 0.
et donc g n'est pas dérivable en 0.