Les fonctions trinômes du second degré ont pour représentation graphique une parabole. Leur étude permet de connaître leur sens de variation, leur maximum ou minimum et la position de leur courbe par rapport à l'axe des abscisses. Ces propriétés se retrouvent algébriquement grâce à la résolution d'équations et d'inéquations du second degré que l'on met au point de manière systématique en classe de première.
1. Qu'est-ce qu'une fonction trinôme du second degré ?
• C'est une fonction f définie sur  par :
par :
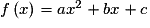 , où a, b et c sont trois réels et
, où a, b et c sont trois réels et 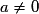 .
.
 par :
par :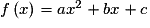 , où a, b et c sont trois réels et
, où a, b et c sont trois réels et 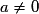 .
.• Lorsque f est mise sous la forme 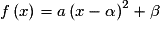 où
où  et
et 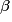 sont des réels dépendants de a, b et c, on dit que f est sous une forme canonique.
sont des réels dépendants de a, b et c, on dit que f est sous une forme canonique.
Exercice n°1
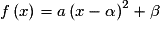 où
où  et
et 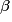 sont des réels dépendants de a, b et c, on dit que f est sous une forme canonique.
sont des réels dépendants de a, b et c, on dit que f est sous une forme canonique.Exercice n°1
2. Quel est le sens de variation d'une fonction trinôme du second degré ?
• La forme canonique de 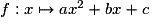 , où
, où 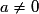 , permet de montrer les résultats suivants :
, permet de montrer les résultats suivants :
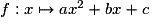 , où
, où 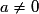 , permet de montrer les résultats suivants :
, permet de montrer les résultats suivants :si a > 0
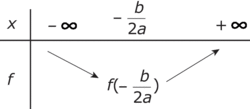 |
si a < 0
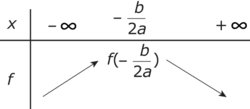 |
• La courbe de f dans un repère du plan est une parabole ayant pour axe de symétrie la droite d'équation 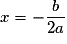 et pour sommetle point
et pour sommetle point 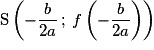 .
.
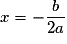 et pour sommetle point
et pour sommetle point 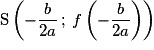 .
.3. Comment résout-on une équation du second degré du type ax2 + bx + c = 0, où a est non nul ?
• Si c = 0, on factorise 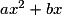 par x et on est ramené à un produit de facteurs nuls.
par x et on est ramené à un produit de facteurs nuls.
Si b = 0, l'équation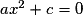 se ramène à l'équation
se ramène à l'équation 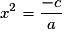 qui se résout facilement selon les signes de c et a.
qui se résout facilement selon les signes de c et a.
Si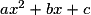 est une identité remarquable évidente, on factorise le trinôme et on est ramené à un produit de facteurs nuls.
est une identité remarquable évidente, on factorise le trinôme et on est ramené à un produit de facteurs nuls.
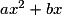 par x et on est ramené à un produit de facteurs nuls.
par x et on est ramené à un produit de facteurs nuls.Si b = 0, l'équation
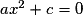 se ramène à l'équation
se ramène à l'équation 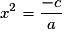 qui se résout facilement selon les signes de c et a.
qui se résout facilement selon les signes de c et a.Si
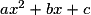 est une identité remarquable évidente, on factorise le trinôme et on est ramené à un produit de facteurs nuls.
est une identité remarquable évidente, on factorise le trinôme et on est ramené à un produit de facteurs nuls.• Dans les autres cas, la forme canonique de 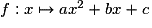 , où
, où 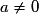 , permet de montrer qu'en calculant le discriminant
, permet de montrer qu'en calculant le discriminant 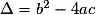 du trinôme
du trinôme 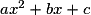 , on a :
, on a :
– si Δ< 0,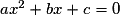 n'a pas de solution dans
n'a pas de solution dans  ;
;
– si Δ= 0,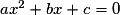 a pour unique solution
a pour unique solution 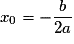 ;
;
– si Δ> 0,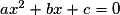 a deux solutions distinctes :
a deux solutions distinctes :
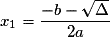 et
et 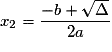 .
.
Exercice n°2
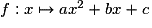 , où
, où 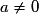 , permet de montrer qu'en calculant le discriminant
, permet de montrer qu'en calculant le discriminant 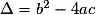 du trinôme
du trinôme 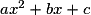 , on a :
, on a :– si Δ< 0,
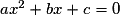 n'a pas de solution dans
n'a pas de solution dans  ;
;– si Δ= 0,
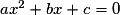 a pour unique solution
a pour unique solution 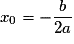 ;
;– si Δ> 0,
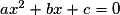 a deux solutions distinctes :
a deux solutions distinctes :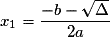 et
et 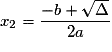 .
.Exercice n°2
• Démonstration :
On a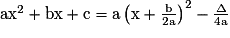
– Si Δ < 0 alors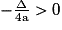 et ainsi
et ainsi 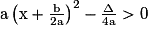 donc ax2 + bx + c > 0 donc l'équation ax2 + bx + c = 0 n'admet aucune solution réelle.
donc ax2 + bx + c > 0 donc l'équation ax2 + bx + c = 0 n'admet aucune solution réelle.
– Si Δ = 0 alors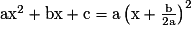 . Ainsi l'équation ax2 + bx + c = 0 est équivalente à l'équation
. Ainsi l'équation ax2 + bx + c = 0 est équivalente à l'équation 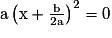
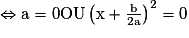 (or
(or 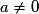 )
)
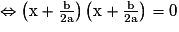
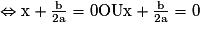
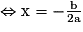
L'équation de départ ax2 + bx + c = 0 admet donc une seule solution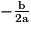 .
.
– Si Δ > 0, alors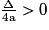 .
.
On a ax2 + bx + c = 0
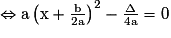
![\Leftrightarrow \mathrm{a}\left [ \left ( \mathrm{x}+\frac{\mathrm{b}}{2\mathrm{a}} \right )^{2}-\frac{\Delta }{4\mathrm{a}^{2}} \right ]= 0](https://static1.assistancescolaire.com/1/images/1s_mat_07_m37.png)
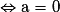 ou
ou 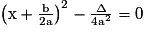 . Or
. Or 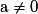 .
.
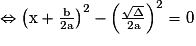
…
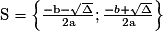
On a
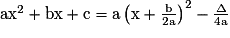
– Si Δ < 0 alors
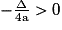 et ainsi
et ainsi 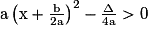 donc ax2 + bx + c > 0 donc l'équation ax2 + bx + c = 0 n'admet aucune solution réelle.
donc ax2 + bx + c > 0 donc l'équation ax2 + bx + c = 0 n'admet aucune solution réelle.– Si Δ = 0 alors
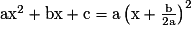 . Ainsi l'équation ax2 + bx + c = 0 est équivalente à l'équation
. Ainsi l'équation ax2 + bx + c = 0 est équivalente à l'équation 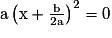
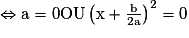 (or
(or 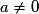 )
)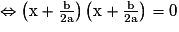
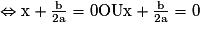
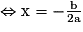
L'équation de départ ax2 + bx + c = 0 admet donc une seule solution
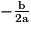 .
.– Si Δ > 0, alors
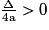 .
.On a ax2 + bx + c = 0
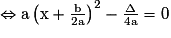
![\Leftrightarrow \mathrm{a}\left [ \left ( \mathrm{x}+\frac{\mathrm{b}}{2\mathrm{a}} \right )^{2}-\frac{\Delta }{4\mathrm{a}^{2}} \right ]= 0](https://static1.assistancescolaire.com/1/images/1s_mat_07_m37.png)
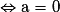 ou
ou 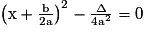 . Or
. Or 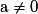 .
.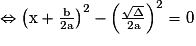
…
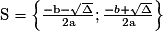
4. Quel algorithme pour résoudre une équation du second degré ?
Algorithme
Variables a, b, c , D, x, y : nombres réels
Début
Lire a, b, c
D b2 − 4ac
b2 − 4ac
Écrire D
Si D < 0 Alors
Écrire « Pas de solution »
Sinon
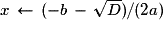
Écrire x
y
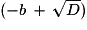 /(2a)
/(2a)
Écrire y
Fin Si
Fin
Variables a, b, c , D, x, y : nombres réels
Début
Lire a, b, c
D
 b2 − 4ac
b2 − 4acÉcrire D
Si D < 0 Alors
Écrire « Pas de solution »
Sinon
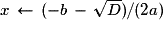
Écrire x
y

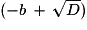 /(2a)
/(2a)Écrire y
Fin Si
Fin
| Sur TI 82 | Sur Graph 25 |
| Input A | ? → A |
| Input B | ? → B |
| Input C | ? → C |
| B2 − 4*A*C Sto D | B2 − 4*A*C → D  |
| Disp D | If D < 0 |
| If D < 0 | Then “PAS DE SOLUTION“ |
| Then | Else (−B +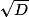 )/(2A) )/(2A)  X X  |
| Disp “PAS DE SOLUTION” | (−B +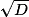 )/(2A) → Y )/(2A) → Y  |
Else 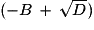 /(2A) /(2A)  X X | Ifend |
| Disp X | |
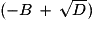 /(2A) /(2A)  Y Y | |
| Disp Y | |
| End |
 |
5. Comment détermine-t-on le signe d'un trinôme du second degré du type ax2 + bx + c, où a est non nul ?
• Si l'équation 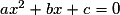 n'a pas de solution dans
n'a pas de solution dans  (Δ< 0), alors
(Δ< 0), alors 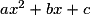 ne se factorise pas et est du signe de a pour tout réel x.
ne se factorise pas et est du signe de a pour tout réel x.
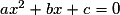 n'a pas de solution dans
n'a pas de solution dans  (Δ< 0), alors
(Δ< 0), alors 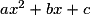 ne se factorise pas et est du signe de a pour tout réel x.
ne se factorise pas et est du signe de a pour tout réel x.• Si l'équation 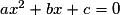 a une unique solution
a une unique solution 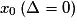 , alors
, alors 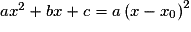 et est du signe de a pour tout
et est du signe de a pour tout 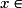

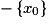 et nul en x0.
et nul en x0.
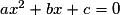 a une unique solution
a une unique solution 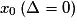 , alors
, alors 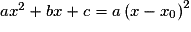 et est du signe de a pour tout
et est du signe de a pour tout 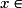

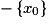 et nul en x0.
et nul en x0.• Si l'équation 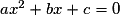 a deux solutions distinctes x1 et x2
a deux solutions distinctes x1 et x2 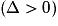 , alors
, alors 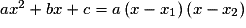 , et un tableau de signes donne le résultat suivant :
, et un tableau de signes donne le résultat suivant :
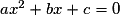 a deux solutions distinctes x1 et x2
a deux solutions distinctes x1 et x2 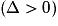 , alors
, alors 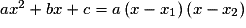 , et un tableau de signes donne le résultat suivant :
, et un tableau de signes donne le résultat suivant :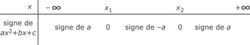 |
6. Quel est le lien entre les solutions d'une équation ou inéquation du second degré et l'allure de la parabole associée ?
• Soit f la fonction définie sur  par
par 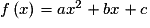 où
où 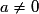 et Cf sa courbe représentative dans un repère du plan.
et Cf sa courbe représentative dans un repère du plan.
Résoudre l'équation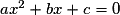 revient à lire graphiquement les abscisses des points d'intersection de Cf et de l'axe des abscisses.
revient à lire graphiquement les abscisses des points d'intersection de Cf et de l'axe des abscisses.
 par
par 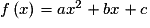 où
où 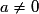 et Cf sa courbe représentative dans un repère du plan.
et Cf sa courbe représentative dans un repère du plan.Résoudre l'équation
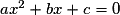 revient à lire graphiquement les abscisses des points d'intersection de Cf et de l'axe des abscisses.
revient à lire graphiquement les abscisses des points d'intersection de Cf et de l'axe des abscisses.• Le signe de 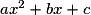 est lié à la position de Cf par rapport à l'axe des abscisses.
est lié à la position de Cf par rapport à l'axe des abscisses.
Voici les différents cas possibles :
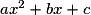 est lié à la position de Cf par rapport à l'axe des abscisses.
est lié à la position de Cf par rapport à l'axe des abscisses.Voici les différents cas possibles :
| a < 0 et Δ< 0 | a < 0 et Δ= 0 | a < 0 et Δ> 0 |
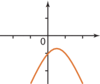 | 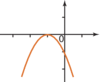 | 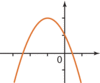 |
| a > 0 et Δ< 0 | a > 0 et Δ= 0 | a > 0 et Δ> 0 |
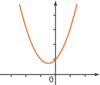 | 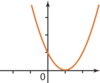 | 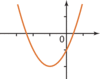 |
À retenir
• Toute fonction trinôme du second degré du type 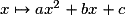 , où
, où 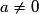 , a pour représentation graphique une parabole de sommet
, a pour représentation graphique une parabole de sommet 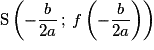 , d'axe de symétrie la droite d'équation
, d'axe de symétrie la droite d'équation 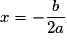 , dont les branches sont « orientées vers le haut » si a > 0 et « orientées vers le bas » si a < 0.
, dont les branches sont « orientées vers le haut » si a > 0 et « orientées vers le bas » si a < 0.
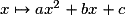 , où
, où 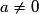 , a pour représentation graphique une parabole de sommet
, a pour représentation graphique une parabole de sommet 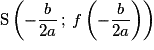 , d'axe de symétrie la droite d'équation
, d'axe de symétrie la droite d'équation 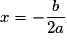 , dont les branches sont « orientées vers le haut » si a > 0 et « orientées vers le bas » si a < 0.
, dont les branches sont « orientées vers le haut » si a > 0 et « orientées vers le bas » si a < 0.• Le signe du discriminant 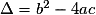 du trinôme
du trinôme 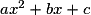 , où
, où 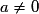 , donne le nombre de solutions à l'équation
, donne le nombre de solutions à l'équation 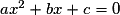 et permet de savoir si le trinôme est factorisable ou non :
et permet de savoir si le trinôme est factorisable ou non :
– si Δ> 0,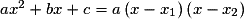 , où
, où 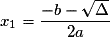 et
et 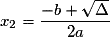 ;
;
– si Δ= 0,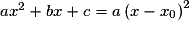 où
où 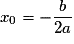 ;
;
– si Δ< 0,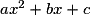 ne se factorise pas, et est du signe de a sur
ne se factorise pas, et est du signe de a sur  .
.
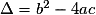 du trinôme
du trinôme 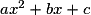 , où
, où 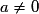 , donne le nombre de solutions à l'équation
, donne le nombre de solutions à l'équation 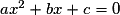 et permet de savoir si le trinôme est factorisable ou non :
et permet de savoir si le trinôme est factorisable ou non :– si Δ> 0,
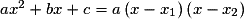 , où
, où 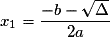 et
et 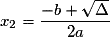 ;
;– si Δ= 0,
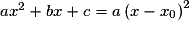 où
où 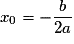 ;
;– si Δ< 0,
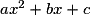 ne se factorise pas, et est du signe de a sur
ne se factorise pas, et est du signe de a sur  .
.Exercice n°1
Cochez la bonne réponse.
Quelle est la forme canonique du trinôme du second degré 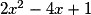 ?
?
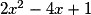 ?
? Cochez la bonne réponse.
| ||
| ||
|
C'est la seule réponse de la forme 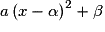 . On a :
. On a : 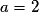 ,
, 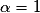 et
et 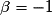 .
.
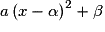 . On a :
. On a : 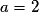 ,
, 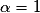 et
et 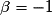 .
.Exercice n°2
Cochez la bonne réponse.
L'équation 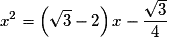 , où
, où 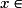
 :
:
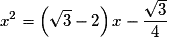 , où
, où 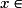
 :
: Cochez la bonne réponse.
| ||
| ||
|
• L'équation 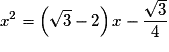 est équivalente à l'équation
est équivalente à l'équation 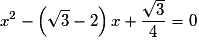 .
.
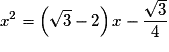 est équivalente à l'équation
est équivalente à l'équation 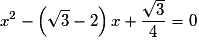 .
.• On calcule le discriminant du trinôme 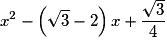 :
:
![\Delta = \left[ { - \left( {\sqrt 3 - 2} \right)} \right]^2 - 4 \times 1 \times \frac{{\sqrt 3 }}{4} = 7 - 4\sqrt 3 - \sqrt 3 = 7 - 5\sqrt 3](https://static1.assistancescolaire.com/1/images/1s_mat_07_m98.png) .
.
Or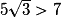 donc le discriminant Δest strictement négatif.
donc le discriminant Δest strictement négatif.
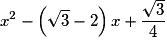 :
:![\Delta = \left[ { - \left( {\sqrt 3 - 2} \right)} \right]^2 - 4 \times 1 \times \frac{{\sqrt 3 }}{4} = 7 - 4\sqrt 3 - \sqrt 3 = 7 - 5\sqrt 3](https://static1.assistancescolaire.com/1/images/1s_mat_07_m98.png) .
.Or
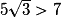 donc le discriminant Δest strictement négatif.
donc le discriminant Δest strictement négatif.• L'équation 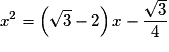 n'a donc aucune solution réelle.
n'a donc aucune solution réelle.
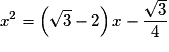 n'a donc aucune solution réelle.
n'a donc aucune solution réelle.Exercice n°3
Cochez la bonne réponse.
Quelles sont les solutions de l'inéquation 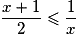 ?
?
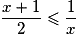 ?
? Cochez la bonne réponse.
| ||
| ||
|
• 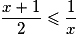 si et seulement si
si et seulement si 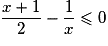 soit
soit 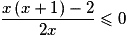 .
.
L'inéquation proposée est donc équivalente à :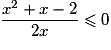 .
.
Or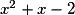 a pour discriminant
a pour discriminant 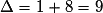 donc
donc 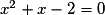 si et seulement si
si et seulement si 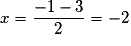 ou
ou 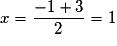 ;
;
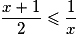 si et seulement si
si et seulement si 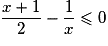 soit
soit 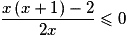 .
.L'inéquation proposée est donc équivalente à :
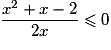 .
.Or
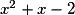 a pour discriminant
a pour discriminant 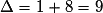 donc
donc 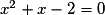 si et seulement si
si et seulement si 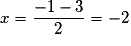 ou
ou 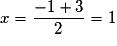 ;
;• On peut alors dresser le tableau des signes suivant :
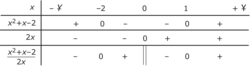 |
On en déduit que ![S = \left] { - \infty \, ; \: - 2} \right] \cup \left] {0 \, ; \: 1} \right]](https://static1.assistancescolaire.com/1/images/1s_mat_07_m114.png) .
.
![S = \left] { - \infty \, ; \: - 2} \right] \cup \left] {0 \, ; \: 1} \right]](https://static1.assistancescolaire.com/1/images/1s_mat_07_m114.png) .
.Exercice n°4
Cochez la bonne réponse.
Quel est l'ensemble des solutions de l'inéquation 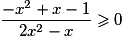 ?
?
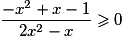 ?
? Cochez la bonne réponse.
| ||
| ||
|
• Le trinôme 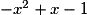 a pour discriminant
a pour discriminant 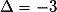 < 0 et
< 0 et 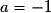 < 0 donc, pour tout
< 0 donc, pour tout 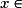
 ,
, 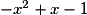 < 0.
< 0.
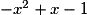 a pour discriminant
a pour discriminant 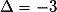 < 0 et
< 0 et 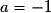 < 0 donc, pour tout
< 0 donc, pour tout 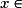
 ,
, 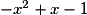 < 0.
< 0.• 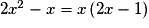 s'annule pour
s'annule pour 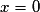 et
et 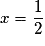 et, puisque
et, puisque 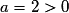 :
:
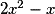 > 0 sur
> 0 sur ![\left] { - \infty \, ; \: 0} \right[ \cup \left] {\frac{1}{2} \, ; \: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m129.png) ;
;
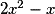 < 0 sur
< 0 sur ![\left] {0 \, ; \: \frac{1}{2}} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m131.png) .
.
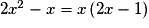 s'annule pour
s'annule pour 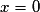 et
et 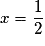 et, puisque
et, puisque 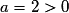 :
: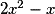 > 0 sur
> 0 sur ![\left] { - \infty \, ; \: 0} \right[ \cup \left] {\frac{1}{2} \, ; \: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m129.png) ;
;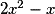 < 0 sur
< 0 sur ![\left] {0 \, ; \: \frac{1}{2}} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m131.png) .
.• Ainsi, ![S = \left] {0 \, ; \: \frac{1}{2}} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m132.png) .
.
![S = \left] {0 \, ; \: \frac{1}{2}} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m132.png) .
.Exercice n°5
Cochez la bonne réponse.
Pour quelles valeurs de m l'équation 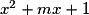 a-t-elle deux solutions distinctes ?
a-t-elle deux solutions distinctes ?
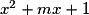 a-t-elle deux solutions distinctes ?
a-t-elle deux solutions distinctes ? Cochez la bonne réponse.
| ||
| ||
|
Le discriminant de 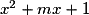 est
est 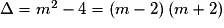 qui est strictement positif si et seulement si
qui est strictement positif si et seulement si 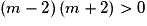 , c'est-à-dire si et seulement si
, c'est-à-dire si et seulement si ![m \in \left] { - \infty \, ; \: - 2} \right[ \cup \left] {2 \, ; \: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m140.png) .
.
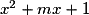 est
est 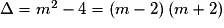 qui est strictement positif si et seulement si
qui est strictement positif si et seulement si 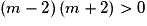 , c'est-à-dire si et seulement si
, c'est-à-dire si et seulement si ![m \in \left] { - \infty \, ; \: - 2} \right[ \cup \left] {2 \, ; \: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m140.png) .
.Exercice n°6
Cochez la bonne réponse.
Laquelle des équations proposées est une équation de la parabole P représentée ci-dessous ?
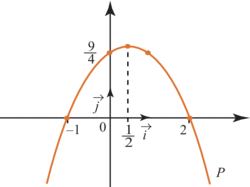 |
Cochez la bonne réponse.
| ||
| ||
|
• La parabole P coupe l'axe des abscisses en  et
et 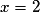 , donc une équation de P est
, donc une équation de P est 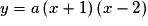 .
.
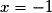 et
et 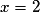 , donc une équation de P est
, donc une équation de P est 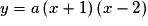 .
.• De plus, P a pour sommet 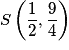 donc
donc 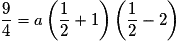 ce qui donne
ce qui donne 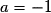 .
.
(Il est logique de trouver a < 0 car P est « tournée vers le bas ».)
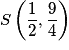 donc
donc 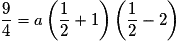 ce qui donne
ce qui donne 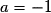 .
.(Il est logique de trouver a < 0 car P est « tournée vers le bas ».)
• D'où P a pour équation 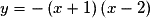 , ou encore
, ou encore 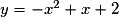 .
.
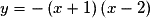 , ou encore
, ou encore 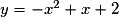 .
.Exercice n°7
Cochez la bonne réponse.
Pour quelles valeurs de k la parabole d'équation 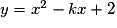 est-elle entièrement au-dessus ou sur l'axe des abscisses ?
est-elle entièrement au-dessus ou sur l'axe des abscisses ?
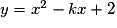 est-elle entièrement au-dessus ou sur l'axe des abscisses ?
est-elle entièrement au-dessus ou sur l'axe des abscisses ? Cochez la bonne réponse.
| ||
| ||
|
• La parabole d'équation 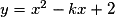 est entièrement au-dessus ou sur l'axe des abscisses si et seulement si, pour tout
est entièrement au-dessus ou sur l'axe des abscisses si et seulement si, pour tout 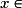
 ,
, 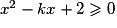 .
.
C'est-à-dire si et seulement si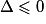 , puisque
, puisque 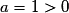 .
.
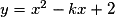 est entièrement au-dessus ou sur l'axe des abscisses si et seulement si, pour tout
est entièrement au-dessus ou sur l'axe des abscisses si et seulement si, pour tout 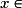
 ,
, 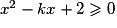 .
.C'est-à-dire si et seulement si
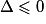 , puisque
, puisque 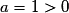 .
.• Or 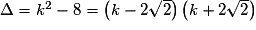 .
.
Donc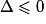 si et seulement si
si et seulement si ![k \in \left[ { - 2\sqrt 2 \, ; \: 2\sqrt 2 } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_07_m164.png) .
.
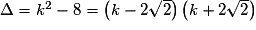 .
.Donc
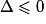 si et seulement si
si et seulement si ![k \in \left[ { - 2\sqrt 2 \, ; \: 2\sqrt 2 } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_07_m164.png) .
.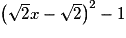
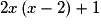
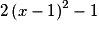
![S = \left] { - \infty \, ; \: - 2} \right] \cup \left] {0 \, ; \: 1} \right]](https://static1.assistancescolaire.com/1/images/1s_mat_07_m102.png)
![S = \left[ { - 2 \, ; \: 0} \right[ \cup \left] {0 \, ; \: 1} \right]](https://static1.assistancescolaire.com/1/images/1s_mat_07_m103.png)
![S = \left] { - \infty \, ; \: 0} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m104.png)
![S = \left] { - \infty \, ; \: 0} \right[ \cup \left] {\frac{1}{2} \, ; \: \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m116.png)
![S = \left] {0 \, ; \: \frac{1}{2}} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m117.png)
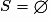
![m \in \left] {2 \, ; \: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m134.png)
![m \in \left] { - 2 \, ; \: + 2} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m135.png)
![m \in \left] { - \infty \, ; \: - 2} \right[ \cup \left] {2 \, ; \: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m136.png)
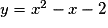
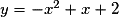
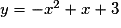
![k \in \left[ { - 2\sqrt 2 \, ; \: 2\sqrt 2 } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_07_m153.png)
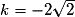 ou
ou 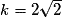
![k \in \left] { - \infty \, ; \: - 2\sqrt 2 } \right] \cup \left[ {2\sqrt 2 \, ; \: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_07_m156.png)

