Pour déterminer la fonction dérivée d'une fonction sur un intervalle donné, on peut revenir à la définition du nombre dérivé en un point a. On calcule alors la limite du taux d'accroissement de cette fonction entre x et a, lorsque x tend vers a. Ce calcul « à la main » est souvent très long et laborieux. Dans la pratique, on calcule une fonction dérivée en utilisant les formules des dérivées des fonctions usuelles, ainsi que les propriétés des opérations sur ces fonctions dérivées.
Les applications de l'étude des fonctions dérivées sont nombreuses. Parmi celles-ci, citons : détermination du sens de variation d'une fonction dérivable sur un intervalle, calcul des extrema locaux, des majorants et minorants éventuels, calcul de limites, etc.
Les applications de l'étude des fonctions dérivées sont nombreuses. Parmi celles-ci, citons : détermination du sens de variation d'une fonction dérivable sur un intervalle, calcul des extrema locaux, des majorants et minorants éventuels, calcul de limites, etc.
1. Quelles sont les fonctions dérivées des fonctions usuelles ?
• La fonction affine 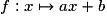 , où a et b sont des réels, est dérivable sur
, où a et b sont des réels, est dérivable sur  et sa fonction dérivée est
et sa fonction dérivée est 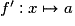 .
.
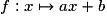 , où a et b sont des réels, est dérivable sur
, où a et b sont des réels, est dérivable sur  et sa fonction dérivée est
et sa fonction dérivée est 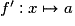 .
.• La fonction puissance 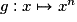 , où
, où 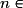
 , est dérivable sur les intervalles où elle est définie (
, est dérivable sur les intervalles où elle est définie (  si
si 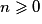 et
et ![\left] { - \infty \, ; \: 0} \right[ \cup \left] {0 \, ; \: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m6.png) si n < 0) et sa fonction dérivée est
si n < 0) et sa fonction dérivée est 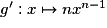 .
.
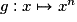 , où
, où 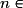
 , est dérivable sur les intervalles où elle est définie (
, est dérivable sur les intervalles où elle est définie (  si
si 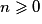 et
et ![\left] { - \infty \, ; \: 0} \right[ \cup \left] {0 \, ; \: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m6.png) si n < 0) et sa fonction dérivée est
si n < 0) et sa fonction dérivée est 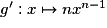 .
.• La fonction racine carrée 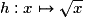 est dérivable sur
est dérivable sur ![\left] {0 \, ; \: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m9.png) et sa fonction dérivée est
et sa fonction dérivée est
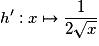 .
.
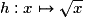 est dérivable sur
est dérivable sur ![\left] {0 \, ; \: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m9.png) et sa fonction dérivée est
et sa fonction dérivée est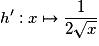 .
.• La fonction cosinus 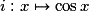 est dérivable sur
est dérivable sur  et sa fonction dérivée est
et sa fonction dérivée est 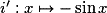 .
.
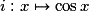 est dérivable sur
est dérivable sur  et sa fonction dérivée est
et sa fonction dérivée est 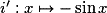 .
.• La fonction sinus 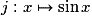 est dérivable sur
est dérivable sur  et sa fonction dérivée est
et sa fonction dérivée est 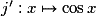 .
.
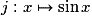 est dérivable sur
est dérivable sur  et sa fonction dérivée est
et sa fonction dérivée est 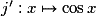 .
.• Les deux premiers résultats permettent de retrouver rapidement ceux qui suivent :
– la fonction constante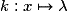 où
où 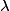 est un réel fixé, est dérivable sur
est un réel fixé, est dérivable sur  et sa fonction dérivée est
et sa fonction dérivée est 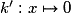 ;
;
– la fonction carré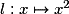 est dérivable sur
est dérivable sur  et sa fonction dérivée est
et sa fonction dérivée est 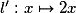 ;
;
– la fonction inverse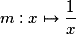 est dérivable sur
est dérivable sur 
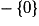 et sa fonction dérivée est
et sa fonction dérivée est 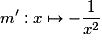 .
.
Exercice n°1
– la fonction constante
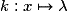 où
où 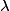 est un réel fixé, est dérivable sur
est un réel fixé, est dérivable sur  et sa fonction dérivée est
et sa fonction dérivée est 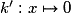 ;
;– la fonction carré
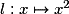 est dérivable sur
est dérivable sur  et sa fonction dérivée est
et sa fonction dérivée est 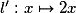 ;
;– la fonction inverse
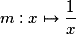 est dérivable sur
est dérivable sur 
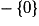 et sa fonction dérivée est
et sa fonction dérivée est 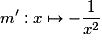 .
.Exercice n°1
2. Comment calculer la dérivée d'une fonction grâce aux opérations sur les fonctions dérivées ?
• Soient u et v deux fonctions dérivables sur un intervalle I ouvert de  . On a les propriétés suivantes :
. On a les propriétés suivantes :
 est dérivable sur I et
est dérivable sur I et 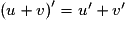 .
.
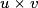 est dérivable sur I et
est dérivable sur I et 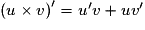 .
.
 . On a les propriétés suivantes :
. On a les propriétés suivantes : est dérivable sur I et
est dérivable sur I et 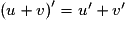 .
.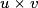 est dérivable sur I et
est dérivable sur I et 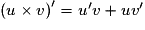 .
.• De ces propriétés, on déduit les suivantes :
– si v ne s'annule pas sur I,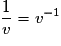 est dérivable sur I et
est dérivable sur I et 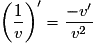 ;
;
– si v ne s'annule pas sur I,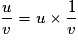 est dérivable sur I et
est dérivable sur I et 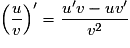 ;
;
– si k est un réel fixé, ku est dérivable sur I et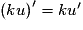 .
.
Exercice n°2Exercice n°3
– si v ne s'annule pas sur I,
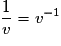 est dérivable sur I et
est dérivable sur I et 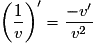 ;
;– si v ne s'annule pas sur I,
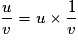 est dérivable sur I et
est dérivable sur I et 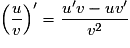 ;
;– si k est un réel fixé, ku est dérivable sur I et
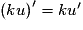 .
.Exercice n°2Exercice n°3
3. Quelle est la fonction dérivée de la fonction composée qui à x associe g (ax + b) ?
Soit f la fonction affine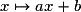 où a et b sont des réels, et g une fonction dérivable sur un intervalle ouvert I. Soit J un intervalle ouvert tel que si
où a et b sont des réels, et g une fonction dérivable sur un intervalle ouvert I. Soit J un intervalle ouvert tel que si 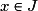 , alors
, alors 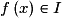 .
.Alors la fonction
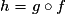 définie sur J par
définie sur J par 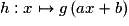 est dérivable sur J et, pour tout
est dérivable sur J et, pour tout 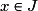 ,
, 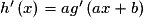 .
.Exercice n°4Exercice n°5
4. Quel est le lien entre la fonction dérivée f' et le sens de variation d'une fonction f dérivable sur un intervalle ouvert ?
Le théorème suivant est admis :Soit f une fonction dérivable sur un intervalle I ouvert de
 . On note f' sa dérivée sur I :
. On note f' sa dérivée sur I :– si
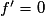 sur I, alors f est constante sur I ;
sur I, alors f est constante sur I ;– si
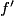 > 0 sur I, sauf éventuellement en un nombre fini de points isolés où
> 0 sur I, sauf éventuellement en un nombre fini de points isolés où 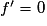 , alors f est strictement croissante sur I ;
, alors f est strictement croissante sur I ;– si
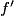 < 0 sur I, sauf éventuellement en un nombre fini de points isolés où
< 0 sur I, sauf éventuellement en un nombre fini de points isolés où 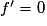 , alors f est strictement décroissante sur I.
, alors f est strictement décroissante sur I.5. Comment détermine-t-on les extrema locaux éventuels d'une fonction dérivable sur un intervalle ouvert ?
Soit f une fonction dérivable sur un intervalle![\left] {a \, ; \: b} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m44.png) de
de  et x0 un réel de cet intervalle.
et x0 un réel de cet intervalle.Si f' s'annule en x0 en changeant de signe, alors f admet un extremum (maximum ou minimum) local en x0.
Remarques
• Le tableau de variation de f permet de visualiser rapidement ces extrema locaux et également de déterminer si ce sont des extrema absolus.
• La recherche d'extrema locaux est utile pour résoudre des problèmes d'optimisation en sciences physiques, en économie, etc.
Exercice n°6
Exercice n°6
6. Comment détermine-t-on une majoration, une minoration ou un encadrement d'une fonction sur un intervalle ?
Soit f une fonction définie sur un intervalle I de .
.Un majorant M de f sur I est un réel tel que, pour tout
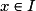 ,
, 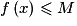 .
.Un minorant m de f sur I est un réel tel que, pour tout
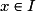 ,
, 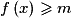 .
.Dans le cas où f admet à la fois un minorant m et un majorant M sur I, alors un encadrement de f sur I est :
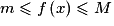 .
.Exercice n°7
7. Comment déterminer une valeur approchée de la solution d'une équation ?
Il existe plusieurs algorithmes permettant de déterminer une valeur approchée d'une solution d'une équation : balayage, dichotomie…La méthode d'Euler utilise le principe de la dérivation.
Algorithme : Méthode de Newton pour résoudre une équation du type f(x)=0
Ici on utilise la fonction f(x) = 0,25x2 − x − 1 et on démarre avec x0 = 3.
 |
Pour epsilon = 0,001 l'affichage final sera 4.828427125049864
Exercice n°5
Exercice n°5
À retenir
• Il faut connaître les formules de dérivées suivantes :
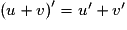
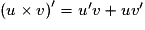
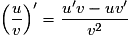
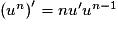 si
si 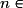
 ou si
ou si 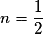
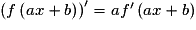
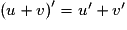
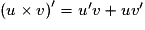
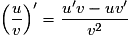
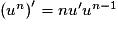 si
si 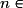
 ou si
ou si 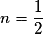
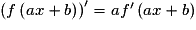
Exercice n°1
Cochez la bonne réponse.
La limite de 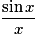 , quand x tend vers 0, est égale à :
, quand x tend vers 0, est égale à :
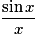 , quand x tend vers 0, est égale à :
, quand x tend vers 0, est égale à : Cochez la bonne réponse.
| ||
| ||
|
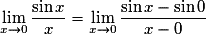
La limite cherchée est donc la limite du taux d'accroissement de la fonction
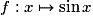 en 0 lorsque x tend vers 0.
en 0 lorsque x tend vers 0.Or f est dérivable sur
 et, pour tout
et, pour tout 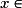
 ,
, 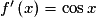 .
.Donc
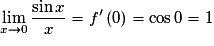 .
.Exercice n°2
Cochez la bonne réponse.
Quelle est, sur  *, la dérivée de la fonction
*, la dérivée de la fonction 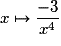 ?
?
 *, la dérivée de la fonction
*, la dérivée de la fonction 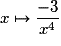 ?
? Cochez la bonne réponse.
| ||
| ||
|
• Posons 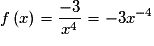 , pour
, pour 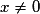 .
.
Donc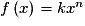 où
où 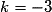 et
et 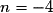 .
.
Ainsi,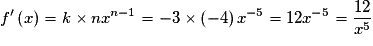 .
.
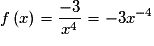 , pour
, pour 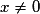 .
.Donc
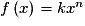 où
où 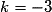 et
et 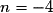 .
.Ainsi,
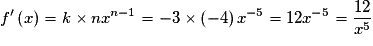 .
.Exercice n°3
Cochez la bonne réponse.
La dérivée de la fonction 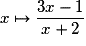 sur
sur ![\left] { - 2\,;\: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m78.png) est la fonction :
est la fonction :
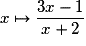 sur
sur ![\left] { - 2\,;\: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m78.png) est la fonction :
est la fonction : Cochez la bonne réponse.
| ||
| ||
|
• Posons 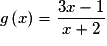 où
où 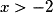 .
.
g est de la forme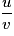 où
où 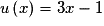 et
et 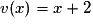 .
.
On a alors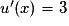 et
et 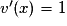 .
.
Ainsi, pour tout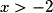 :
:
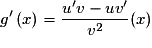
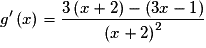
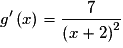
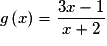 où
où 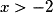 .
.g est de la forme
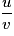 où
où 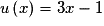 et
et 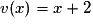 .
.On a alors
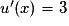 et
et 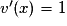 .
.Ainsi, pour tout
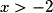 :
: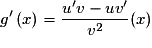
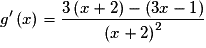
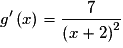
Exercice n°4
Cochez la bonne réponse.
La dérivée de la fonction 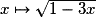 sur
sur ![\left] { - \infty \, ; \: \frac{1}{3}} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m94.png) est la fonction :
est la fonction :
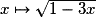 sur
sur ![\left] { - \infty \, ; \: \frac{1}{3}} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m94.png) est la fonction :
est la fonction : Cochez la bonne réponse.
| ||
| ||
|
• Posons 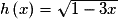 pour x <
pour x < 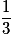 .
.
h est telle que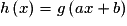 , avec
, avec 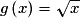 ,
, 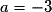 et
et 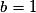 .
.
Donc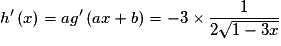 , puisque
, puisque 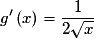 .
.
D'où, pour tout![x \in \left] { - \infty \,;\: \frac{1}{3}} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m106.png) ,
, 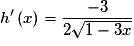 .
.
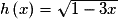 pour x <
pour x < 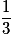 .
.h est telle que
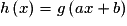 , avec
, avec 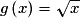 ,
, 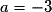 et
et 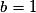 .
.Donc
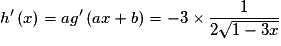 , puisque
, puisque 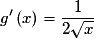 .
.D'où, pour tout
![x \in \left] { - \infty \,;\: \frac{1}{3}} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m106.png) ,
, 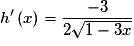 .
.Exercice n°5
Cochez la bonne réponse.
Quelle est la dérivée de la fonction 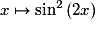 sur
sur  ?
?
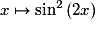 sur
sur  ?
? Cochez la bonne réponse.
| ||
| ||
|
• Posons ![m(x) = \sin ^2 (2x) = \left[ {\sin \left( {2x} \right)} \right]^2](https://static1.assistancescolaire.com/1/images/1s_mat_09_m112.png) .
.
m est de la forme un où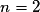 et
et 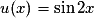 .
.
u est de la forme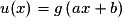 , avec
, avec 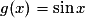 ,
, 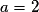 et
et 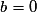 .
.
![m(x) = \sin ^2 (2x) = \left[ {\sin \left( {2x} \right)} \right]^2](https://static1.assistancescolaire.com/1/images/1s_mat_09_m112.png) .
.m est de la forme un où
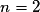 et
et 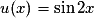 .
.u est de la forme
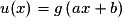 , avec
, avec 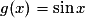 ,
, 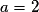 et
et 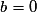 .
.• On a 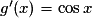 , d'où
, d'où 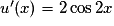 .
.
Ainsi,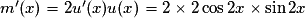 ;
;
d'où, pour tout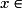
 ,
, 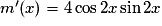 .
.
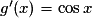 , d'où
, d'où 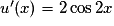 .
.Ainsi,
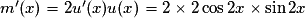 ;
;d'où, pour tout
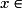
 ,
, 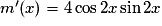 .
.Exercice n°6
Cochez la bonne réponse.
La fonction 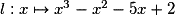 définie sur
définie sur  admet :
admet :
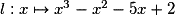 définie sur
définie sur  admet :
admet : Cochez la bonne réponse.
| ||
| ||
|
• La fonction l est dérivable sur  et, pour tout
et, pour tout 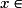
 ,
, 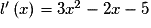 . On a affaire à un trinôme du second degré dont le discriminant est :
. On a affaire à un trinôme du second degré dont le discriminant est : 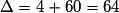 .
.
Donc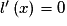 pour
pour 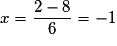 et
et 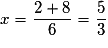 .
.
Comme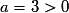 , alors :
, alors :
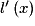 > 0 pour
> 0 pour ![x \in \left] { - \infty \, ; \: - 1} \right[ \cup \left] {\frac{5}{3}\,;\: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m136.png) ;
;
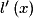 < 0 pour
< 0 pour ![x \in \left] { - 1\,;\:\frac{5}{3}} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m138.png) .
.
 et, pour tout
et, pour tout 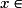
 ,
, 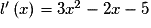 . On a affaire à un trinôme du second degré dont le discriminant est :
. On a affaire à un trinôme du second degré dont le discriminant est : 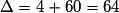 .
.Donc
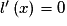 pour
pour 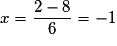 et
et 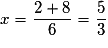 .
.Comme
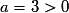 , alors :
, alors :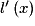 > 0 pour
> 0 pour ![x \in \left] { - \infty \, ; \: - 1} \right[ \cup \left] {\frac{5}{3}\,;\: + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m136.png) ;
;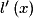 < 0 pour
< 0 pour ![x \in \left] { - 1\,;\:\frac{5}{3}} \right[](https://static1.assistancescolaire.com/1/images/1s_mat_09_m138.png) .
.• On en déduit le tableau de variation de l :
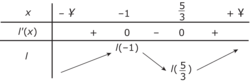 |
On en déduit que l admet un maximum local en 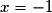 (et un minimum local en
(et un minimum local en 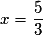 ).
).
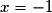 (et un minimum local en
(et un minimum local en 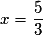 ).
).Exercice n°7
Cochez la bonne réponse.
Que peut-on dire des variations et du signe de la fonction 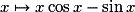 ?
?
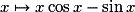 ?
? Cochez la bonne réponse.
| ||
| ||
|
• La fonction 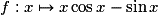 est dérivable sur
est dérivable sur ![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m146.png) comme somme des fonctions
comme somme des fonctions  , dérivable sur
, dérivable sur  donc sur
donc sur ![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m148.png) , et
, et 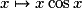 , dérivable sur
, dérivable sur  , donc sur
, donc sur ![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m150.png) , cette seconde fonction étant le produit de fonctions dérivables sur
, cette seconde fonction étant le produit de fonctions dérivables sur  , donc sur
, donc sur ![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m151.png) .
.
Et, pour tout![x \in \left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m152.png) ,
, 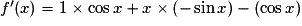 ,
,
soit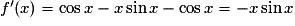 .
.
Or sur![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m155.png) ,
, 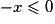 et
et 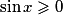 donc
donc 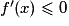 . Plus précisément,
. Plus précisément, 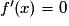 si et seulement si
si et seulement si 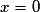 ou
ou  .
.
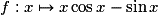 est dérivable sur
est dérivable sur ![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m146.png) comme somme des fonctions
comme somme des fonctions  , dérivable sur
, dérivable sur  donc sur
donc sur ![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m148.png) , et
, et 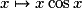 , dérivable sur
, dérivable sur  , donc sur
, donc sur ![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m150.png) , cette seconde fonction étant le produit de fonctions dérivables sur
, cette seconde fonction étant le produit de fonctions dérivables sur  , donc sur
, donc sur ![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m151.png) .
.Et, pour tout
![x \in \left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m152.png) ,
, 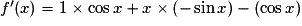 ,
,soit
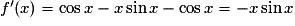 .
.Or sur
![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m155.png) ,
, 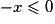 et
et 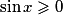 donc
donc 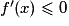 . Plus précisément,
. Plus précisément, 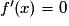 si et seulement si
si et seulement si 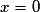 ou
ou  .
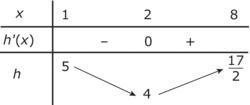
.• On en déduit le tableau de variation suivant :
 |
Ainsi, pour tout ![x \in \left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m162.png) ,
, 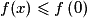 donc
donc 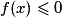 .
.
Donc f est strictement décroissante et négative sur![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m165.png) . (0 est le maximum de f sur
. (0 est le maximum de f sur ![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m166.png) .)
.)
![x \in \left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m162.png) ,
, 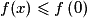 donc
donc 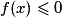 .
.Donc f est strictement décroissante et négative sur
![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m165.png) . (0 est le maximum de f sur
. (0 est le maximum de f sur ![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m166.png) .)
.)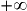 quand
quand 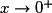 et
et 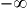 quand
quand 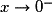
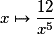
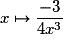
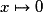
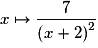
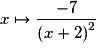
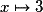
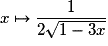
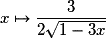
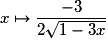
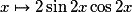
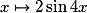
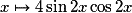
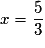
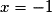
![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m142.png)
![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m143.png)
![\left[ {0\,;\:\pi } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_09_m144.png)

