Mouvements de satellites et de planètes : les trois lois de Kepler
L'objectif de ce chapitre est d'étudier le mouvement des objets célestes dans notre système solaire : comètes, satellites, planètes, etc. Pour cela, on utilise notamment les lois de Kepler, qui caractérisent le mouvement des planètes autour du Soleil. On peut retrouver ces lois en utilisant l'expression de la gravitation universelle.
I. Qu'est-ce qu'un référentiel héliocentrique ?
Les lois de Kepler s'appliquent dans le référentiel héliocentrique qui est galiléen. Celui-ci est constitué du centre du Soleil et de trois étoiles lointaines. Ce référentiel est utilisé pour étudier le mouvement des planètes de notre système solaire.
II. Qu'est-ce la première loi de Kepler (ou loi des orbites) ?
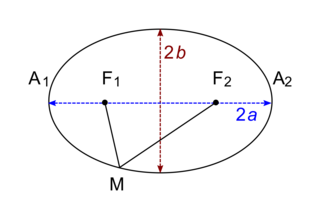 |
Dans le référentiel héliocentrique, le centre de chaque planète décrit une trajectoire elliptique dont le Soleil S est l'un des foyers :
• a est appelé demi-grand axe de l'ellipse ;
• b est appelé demi-petit axe de l'ellipse ;
• F1 et F2 sont les foyers de l'ellipse.
Une ellipse est formée par l'ensemble des points dont la somme des distances à deux points fixes est constante : MF1 + MF2 = A1A2 = 2a.
Toutes les planètes du système solaire (excepté Mercure) ont des trajectoires quasi circulaires.
Toutes les planètes du système solaire (excepté Mercure) ont des trajectoires quasi circulaires.
III. Qu'est-ce que la deuxième loi de Kepler (ou loi des aires) ?
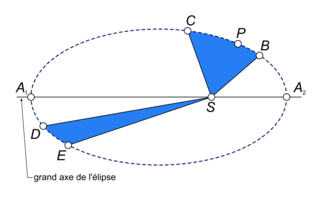 |
Le segment reliant le Soleil à une planète balaie des aires égales pendant des durées égales.
Ici, la portion d'ellipse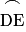 est parcourue dans le même temps que la portion
est parcourue dans le même temps que la portion 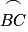 , ce qui implique que la planète va plus vite quand elle est proche d'un foyer de l'ellipse que quand elle en est loin.
, ce qui implique que la planète va plus vite quand elle est proche d'un foyer de l'ellipse que quand elle en est loin.
Ici, la portion d'ellipse
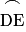 est parcourue dans le même temps que la portion
est parcourue dans le même temps que la portion 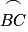 , ce qui implique que la planète va plus vite quand elle est proche d'un foyer de l'ellipse que quand elle en est loin.
, ce qui implique que la planète va plus vite quand elle est proche d'un foyer de l'ellipse que quand elle en est loin.IV. Qu'est-ce que la troisième loi de Kepler (ou loi des périodes) ?
Pour toute planète du système solaire, le rapport entre le carré de la période de révolution et le cube du demi-grand axe est le même et vaut 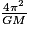 . Elle est appelée « constante de la loi des aires ». Sa valeur ne dépend pas de la planète considérée, mais uniquement de la masse de l'étoile autour de laquelle elle gravite (ici, le Soleil). On a :
. Elle est appelée « constante de la loi des aires ». Sa valeur ne dépend pas de la planète considérée, mais uniquement de la masse de l'étoile autour de laquelle elle gravite (ici, le Soleil). On a :
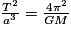 .
.
Remarque : On peut étendre l'application des lois Kepler à tous les systèmes planète-étoile ou satellite-planète. L'origine du repère à choisir est alors le centre de l'objet le plus lourd, à savoir l'étoile dans un système planète-étoile, et la planète dans un système satellite-planète.
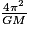 . Elle est appelée « constante de la loi des aires ». Sa valeur ne dépend pas de la planète considérée, mais uniquement de la masse de l'étoile autour de laquelle elle gravite (ici, le Soleil). On a :
. Elle est appelée « constante de la loi des aires ». Sa valeur ne dépend pas de la planète considérée, mais uniquement de la masse de l'étoile autour de laquelle elle gravite (ici, le Soleil). On a :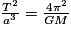 .
.Remarque : On peut étendre l'application des lois Kepler à tous les systèmes planète-étoile ou satellite-planète. L'origine du repère à choisir est alors le centre de l'objet le plus lourd, à savoir l'étoile dans un système planète-étoile, et la planète dans un système satellite-planète.
V. Comment étudier la rotation de la Terre autour du Soleil ?
Pour étudier le mouvement d'une planète autour du Soleil, il faut choisir :
• le référentiel : héliocentrique, galiléen ;
• le système : la Terre.
 |
Appliquons la relation fondamentale de la dynamique à notre système.
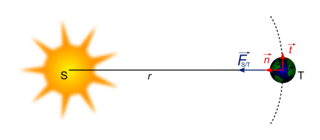
On note mT la masse de la Terre, mS la masse du Soleil, et r la distance séparant leurs centres d'inertie. La seule force s'exerçant sur la Terre est la force de gravitation universelle :
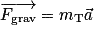 .
.
Projetons dans la base de Frenet :
On note mT la masse de la Terre, mS la masse du Soleil, et r la distance séparant leurs centres d'inertie. La seule force s'exerçant sur la Terre est la force de gravitation universelle :
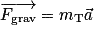 .
.Projetons dans la base de Frenet :
• selon 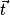 : la force de gravitation étant radiale, elle n'a pas de composante sur cet axe et at = 0.
: la force de gravitation étant radiale, elle n'a pas de composante sur cet axe et at = 0.
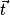 : la force de gravitation étant radiale, elle n'a pas de composante sur cet axe et at = 0.
: la force de gravitation étant radiale, elle n'a pas de composante sur cet axe et at = 0.• selon 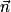 :
: 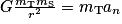 , d'où
, d'où 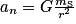 .
.
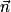 :
: 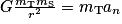 , d'où
, d'où 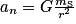 .
.L'accélération du centre d'inertie de la planète Terre est radiale, centripète et indépendante de la masse de la planète elle-même.
Or, dans la base de Frenet,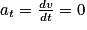 . Cela implique que la vitesse de la planète est constante. Le mouvement est donc circulaire et uniforme.
. Cela implique que la vitesse de la planète est constante. Le mouvement est donc circulaire et uniforme.
De plus, dans la base de Frenet,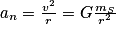 . On peut donc en déduire que
. On peut donc en déduire que 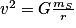 , soit
, soit 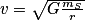 .
.
Or, on sait que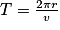 , donc
, donc 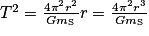 .
.
D'où la troisième loi de Kepler :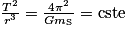 . La constante ne dépend que de la masse du Soleil.
. La constante ne dépend que de la masse du Soleil.
Or, dans la base de Frenet,
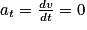 . Cela implique que la vitesse de la planète est constante. Le mouvement est donc circulaire et uniforme.
. Cela implique que la vitesse de la planète est constante. Le mouvement est donc circulaire et uniforme.De plus, dans la base de Frenet,
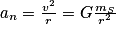 . On peut donc en déduire que
. On peut donc en déduire que 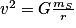 , soit
, soit 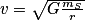 .
.Or, on sait que
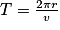 , donc
, donc 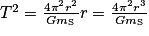 .
.D'où la troisième loi de Kepler :
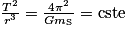 . La constante ne dépend que de la masse du Soleil.
. La constante ne dépend que de la masse du Soleil.VI. Que fait un satellite tournant autour de la Terre ?
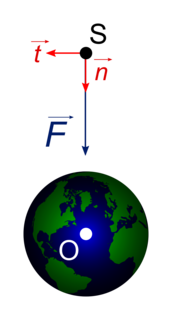 |
Pour étudier le mouvement d'un satellite autour de la Terre, on choisit le référentiel géocentrique galiléen et le système {satellite} est assimilé au point matériel S.
Appliquons la relation fondamentale de la dynamique à notre système. On note mT la masse et RT le rayon de la Terre, mS la masse du satellite et r la distance séparant leurs centres d'inertie. La seule force s'exerçant sur le satellite est la force de gravitation universelle :
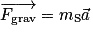 .
.
Projetons dans la base de Frenet :
Appliquons la relation fondamentale de la dynamique à notre système. On note mT la masse et RT le rayon de la Terre, mS la masse du satellite et r la distance séparant leurs centres d'inertie. La seule force s'exerçant sur le satellite est la force de gravitation universelle :
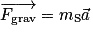 .
.Projetons dans la base de Frenet :
• selon 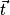 : la force de gravitation étant radiale, elle n'a pas de composante sur cet axe et at = 0.
: la force de gravitation étant radiale, elle n'a pas de composante sur cet axe et at = 0.
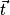 : la force de gravitation étant radiale, elle n'a pas de composante sur cet axe et at = 0.
: la force de gravitation étant radiale, elle n'a pas de composante sur cet axe et at = 0.• selon 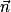 :
: 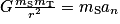 , d'où
, d'où 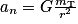 .
.
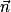 :
: 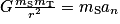 , d'où
, d'où 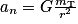 .
.La vitesse du satellite est constante. Le mouvement du satellite est donc circulaire et uniforme.
De plus, dans la base de Frenet,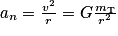 . On peut donc en déduire (si on pose
. On peut donc en déduire (si on pose 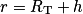 , où h représente l'altitude du satellite par rapport au sol) que :
, où h représente l'altitude du satellite par rapport au sol) que :
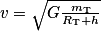 .
.
On a également la période de révolution T du satellite qui vérifie :
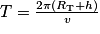 , d'où
, d'où 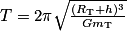 .
.
La vitesse et la période du satellite, caractéristiques du mouvement du satellite, ne dépendent que de l'altitude de celui-ci : elles ne dépendent pas de sa masse.
De plus, dans la base de Frenet,
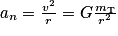 . On peut donc en déduire (si on pose
. On peut donc en déduire (si on pose 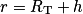 , où h représente l'altitude du satellite par rapport au sol) que :
, où h représente l'altitude du satellite par rapport au sol) que :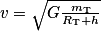 .
.On a également la période de révolution T du satellite qui vérifie :
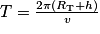 , d'où
, d'où 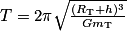 .
.La vitesse et la période du satellite, caractéristiques du mouvement du satellite, ne dépendent que de l'altitude de celui-ci : elles ne dépendent pas de sa masse.
Zoom sur…
La force de gravitation universelle
La loi de la gravitation découverte par Isaac Newton permet de décrire par une même expression l'attraction entre deux corps massiques.Deux corps de masse mA et mB, dont les centres de masse sont séparés par une distance AB, exercent l'un sur l'autre des forces attractives
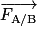 et
et 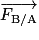 de même direction, de sens opposés, et de même valeur :
de même direction, de sens opposés, et de même valeur :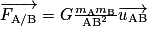 , avec
, avec 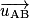 vecteur unitaire orienté de A vers B.
vecteur unitaire orienté de A vers B.Sur Terre, on approxime cette loi par le poids. En effet, l'accélération de pesanteur que l'on note g correspond en fait à la valeur
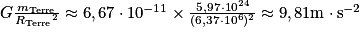 . Cette approximation reste valable tant que l'objet étudié est à une distance de la Terre négligeable devant son rayon (cela ne fonctionne pas pour les satellites en rotation autour de la Terre, par exemple).
. Cette approximation reste valable tant que l'objet étudié est à une distance de la Terre négligeable devant son rayon (cela ne fonctionne pas pour les satellites en rotation autour de la Terre, par exemple).Les satellites géostationnaires
On appelle satellite géostationnaire tout satellite fixe (stationnaire) par rapport à la Terre (géo), dans le sens où il reste alors toujours au-dessus de la même zone de la planète. Pour cela, il faut :
• qu'il décrive un mouvement circulaire uniforme dans un plan perpendiculaire à l'axe des pôles terrestres. Il évolue donc dans un plan équatorial (plan contenant l'équateur) ;
• qu'il tourne dans le même sens que la Terre autour de l'axe de ses pôles ;
• que sa période de révolution soit exactement égale à la période de rotation de la Terre autour de l'axe de ses pôles (24 heures environ).
L'altitude à laquelle le satellite doit se situer pour satisfaire cette dernière condition est donc :
![h=\sqrt[3]{\frac{Gm_{\textrm{T}}T^{2}}{4\pi ^{2}}}-R_{\textrm{T}}](https://static1.assistancescolaire.com/t/images/t_speph_08_m32.png) .
.
L'application numérique donne : h = 36 × 106 m, soit 3 816 000 km.
![h=\sqrt[3]{\frac{Gm_{\textrm{T}}T^{2}}{4\pi ^{2}}}-R_{\textrm{T}}](https://static1.assistancescolaire.com/t/images/t_speph_08_m32.png) .
.L'application numérique donne : h = 36 × 106 m, soit 3 816 000 km.

