Lois de Newton, quantité de mouvement et conservation de l'énergie mécanique
On appelle force toute action mécanique d'un corps sur un autre, capable de produire des effets sur le mouvement ou la forme de celui-ci. Toute force est soumise à des lois physiques découvertes par Newton. Ces lois régissent tous les mouvements en mécanique classique, c'est-à-dire à tous les mouvements macroscopiques de notre monde : elles permettent de les décrire par des équations.
I. Qu'est-ce que la première loi de Newton (ou principe d'inertie) ?
Lorsqu'un solide est isolé ou pseudo-isolé, il existe toujours un point particulier G du solide, appelé centre d'inertie, qui est :• soit au repos, s'il est initialement au repos : 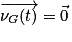 ;
;
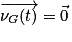 ;
;• soit être animé d'un mouvement rectiligne uniforme :
Un solide est pseudo-isolé lorsque les forces agissant sur lui se compensent :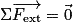 .
.
Ce principe n'est valable que dans les référentiels galiléens ; les référentiels terrestre, géocentrique et héliocentrique en sont des exemples. Tout autre référentiel dans lequel le principe de l'inertie est vérifié est dit galiléen. Cela implique que les référentiels galiléens sont en translation rectiligne uniforme les uns par rapport aux autres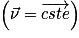 .
.
Un solide est pseudo-isolé lorsque les forces agissant sur lui se compensent :
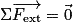 .
.Ce principe n'est valable que dans les référentiels galiléens ; les référentiels terrestre, géocentrique et héliocentrique en sont des exemples. Tout autre référentiel dans lequel le principe de l'inertie est vérifié est dit galiléen. Cela implique que les référentiels galiléens sont en translation rectiligne uniforme les uns par rapport aux autres
 .
.II. Qu'est-ce que la troisième loi de Newton (ou principe d'action-réaction) ?
Lorsqu'un solide A exerce sur un solide B une force 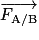 (action), alors le solide B exerce sur le solide A une force
(action), alors le solide B exerce sur le solide A une force 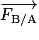 (réaction) telle que :
(réaction) telle que :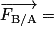
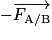 .
.
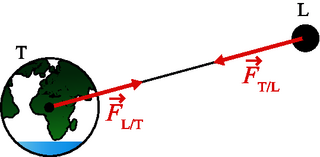
Dans tout référentiel, les corps étant immobiles ou animés de mouvements quelconques, ces deux forces ont même intensité, même droite d'action, mais elles sont de sens contraires.
Exemple : La Terre exerce sur la Lune une force qui a même direction, même intensité, mais est contraire à celle exercée par la Lune sur la Terre.
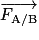 (action), alors le solide B exerce sur le solide A une force
(action), alors le solide B exerce sur le solide A une force 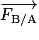 (réaction) telle que :
(réaction) telle que :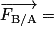
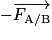 .
.Dans tout référentiel, les corps étant immobiles ou animés de mouvements quelconques, ces deux forces ont même intensité, même droite d'action, mais elles sont de sens contraires.
Exemple : La Terre exerce sur la Lune une force qui a même direction, même intensité, mais est contraire à celle exercée par la Lune sur la Terre.
 |
III. Quelles sont les principales forces usuelles ?
La force poids 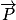 correspond à l'approximation de l'interaction gravitationnelle entre la Terre et les objets proches d'elle. C'est une action à distance, toujours attractive, et qui existe même lorsque le système n'est pas en contact avec le sol. Elle est répartie dans tout le volume du système. En pratique, on ne représente que sa résultante, qui est la somme vectorielle de toutes les petites forces qui s'exercent sur chaque point du système, et on la place au centre de gravité de l'objet.
correspond à l'approximation de l'interaction gravitationnelle entre la Terre et les objets proches d'elle. C'est une action à distance, toujours attractive, et qui existe même lorsque le système n'est pas en contact avec le sol. Elle est répartie dans tout le volume du système. En pratique, on ne représente que sa résultante, qui est la somme vectorielle de toutes les petites forces qui s'exercent sur chaque point du système, et on la place au centre de gravité de l'objet.
Sa résultante s'écrit :
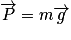 .
.
Caractéristiques :
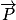 correspond à l'approximation de l'interaction gravitationnelle entre la Terre et les objets proches d'elle. C'est une action à distance, toujours attractive, et qui existe même lorsque le système n'est pas en contact avec le sol. Elle est répartie dans tout le volume du système. En pratique, on ne représente que sa résultante, qui est la somme vectorielle de toutes les petites forces qui s'exercent sur chaque point du système, et on la place au centre de gravité de l'objet.
correspond à l'approximation de l'interaction gravitationnelle entre la Terre et les objets proches d'elle. C'est une action à distance, toujours attractive, et qui existe même lorsque le système n'est pas en contact avec le sol. Elle est répartie dans tout le volume du système. En pratique, on ne représente que sa résultante, qui est la somme vectorielle de toutes les petites forces qui s'exercent sur chaque point du système, et on la place au centre de gravité de l'objet.Sa résultante s'écrit :
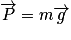 .
.Caractéristiques :
• point d'application : en G, centre de gravité du système étudié ;
• direction : verticale ;
• sens : vers le centre de la Terre ;
• intensité : P = m × g, avec P en newton, g en 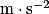 et m en kg.
et m en kg.
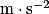 et m en kg.
et m en kg.La force électrostatique 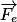 se définit de la manière suivante : une charge q placée dans un champ électrostatique
se définit de la manière suivante : une charge q placée dans un champ électrostatique  subit une force
subit une force 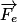 telle que
telle que 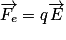 . La force
. La force 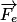 et le champ électrique
et le champ électrique 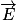 ont même sens si la charge est positive, et sont de sens opposés si la charge est négative.
ont même sens si la charge est positive, et sont de sens opposés si la charge est négative.
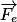 se définit de la manière suivante : une charge q placée dans un champ électrostatique
se définit de la manière suivante : une charge q placée dans un champ électrostatique  subit une force
subit une force 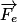 telle que
telle que 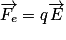 . La force
. La force 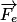 et le champ électrique
et le champ électrique 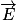 ont même sens si la charge est positive, et sont de sens opposés si la charge est négative.
ont même sens si la charge est positive, et sont de sens opposés si la charge est négative.IV. Qu'est-ce que la deuxième loi de Newton (ou relation fondamentale de la dynamique) ?
Dans le cas où les forces extérieures appliquées à un système ne se compensent pas, alors le système voit son état de repos ou de mouvement modifié, car il n'est plus isolé ou pseudo-isolé.Dans un référentiel galiléen, la somme des forces extérieures qui s'appliquent au système est égale au changement de quantité de mouvement par unité de temps :
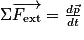 . Si la masse est constante au cours du temps, la deuxième loi de Newton se simplifie :
. Si la masse est constante au cours du temps, la deuxième loi de Newton se simplifie :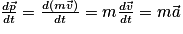 .
.Soit :
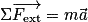 .
.V. Comment appliquer les lois de Newton à un champ de force uniforme, comme le champ de pesanteur ?
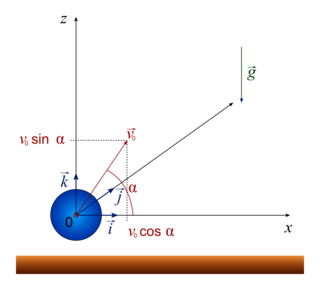 |
Soit un solide soumis à son seul poids 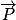 et lancé avec une vitesse initiale
et lancé avec une vitesse initiale 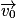 non nulle.
non nulle.
En se plaçant dans le référentiel terrestre supposé galiléen, d'après la deuxième loi de Newton, on a :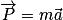 soit
soit 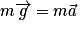 .
.
On a donc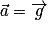 .
.
Choisissons un repère orthonormé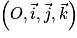 tel que la position initiale coïncide avec le centre O du repère et tel que le vecteur initial
tel que la position initiale coïncide avec le centre O du repère et tel que le vecteur initial 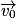 soit dans le plan vertical.
soit dans le plan vertical.
Dans le repère choisi, le vecteur champ de pesanteur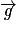 est colinéaire de sens opposé à
est colinéaire de sens opposé à 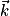 donc :
donc :
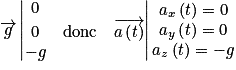
Comme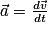 , on primitive le système d'équations, et on obtient :
, on primitive le système d'équations, et on obtient :
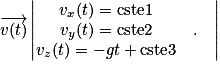
Les constantes cste1, cste2, cste3 sont déterminées par les conditions initiales.
À t = 0, on a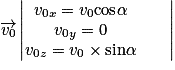 , avec α l'angle entre
, avec α l'angle entre 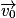 et l'axe Ox.
et l'axe Ox.
Donc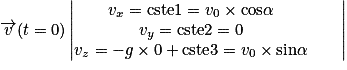 . On en déduit donc que :
. On en déduit donc que :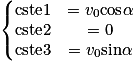
On obtient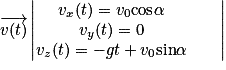 .
.
Comme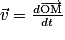 , on primitive le système d'équations, et on obtient :
, on primitive le système d'équations, et on obtient :
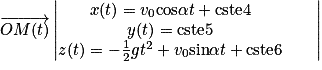
Les constantes cste4, cste5, cste6 sont déterminées par les conditions initiales.
À t = 0, le point M est à l'origine du repère donc cste4 = cste5 = cste6 = 0.
On obtient alors les équations horaires du mouvement :
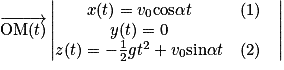 .
.
Quel que soit l'instant t, on a y = 0 : la trajectoire est donc décrite dans le plan (Ox, Oz).
D'après (1), on a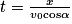 .
.
En injectant cette relation dans (2), on en déduit l'équation de la trajectoire :
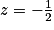
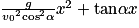 .
.
La trajectoire est plane et parabolique.
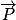 et lancé avec une vitesse initiale
et lancé avec une vitesse initiale 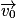 non nulle.
non nulle.En se plaçant dans le référentiel terrestre supposé galiléen, d'après la deuxième loi de Newton, on a :
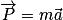 soit
soit 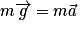 .
.On a donc
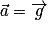 .
.Choisissons un repère orthonormé
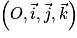 tel que la position initiale coïncide avec le centre O du repère et tel que le vecteur initial
tel que la position initiale coïncide avec le centre O du repère et tel que le vecteur initial 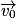 soit dans le plan vertical.
soit dans le plan vertical.Dans le repère choisi, le vecteur champ de pesanteur
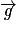 est colinéaire de sens opposé à
est colinéaire de sens opposé à 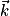 donc :
donc :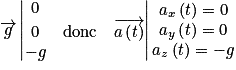
Comme
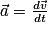 , on primitive le système d'équations, et on obtient :
, on primitive le système d'équations, et on obtient :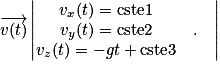
Les constantes cste1, cste2, cste3 sont déterminées par les conditions initiales.
À t = 0, on a
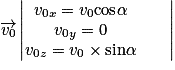 , avec α l'angle entre
, avec α l'angle entre 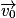 et l'axe Ox.
et l'axe Ox.Donc
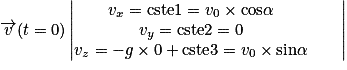 . On en déduit donc que :
. On en déduit donc que :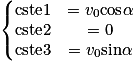
On obtient
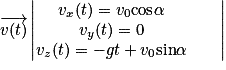 .
.Comme
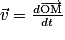 , on primitive le système d'équations, et on obtient :
, on primitive le système d'équations, et on obtient :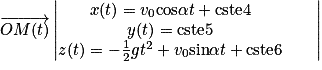
Les constantes cste4, cste5, cste6 sont déterminées par les conditions initiales.
À t = 0, le point M est à l'origine du repère donc cste4 = cste5 = cste6 = 0.
On obtient alors les équations horaires du mouvement :
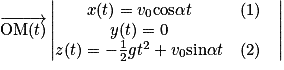 .
.Quel que soit l'instant t, on a y = 0 : la trajectoire est donc décrite dans le plan (Ox, Oz).
D'après (1), on a
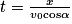 .
.En injectant cette relation dans (2), on en déduit l'équation de la trajectoire :
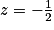
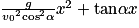 .
.La trajectoire est plane et parabolique.
VI. Qu'est-ce que la conservation de l'énergie dans un champ de force uniforme ?
De façon générale, on définit l'énergie mécanique d'un système comme la somme de son énergie cinétique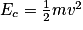 , et de son énergie potentielle Ep définie par rapport à un référentiel :
, et de son énergie potentielle Ep définie par rapport à un référentiel :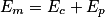 .
.Dans le cas d'un objet dans un champ de pesanteur uniforme, l'énergie potentielle du système étudié vaut Epp = mgz, avec z la position selon la direction du vecteur
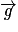 .
.Dans le cas d'un objet dans un champ électrique uniforme, l'énergie potentielle du système étudié vaut Epp = qEy, avec y la position selon l'axe du vecteur
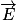 .
.Lorsque le système n'est soumis qu'à des forces conservatives, l'énergie mécanique se conserve, c'est-à-dire que la variation d'énergie mécanique est nulle. On a alors ΔEm = 0. Il y a transformation d'énergie potentielle en énergie cinétique, ou inversement. Cette relation permet d'évaluer la vitesse ou la position d'un objet, à des instants précis.
Notion clé
La quantité de mouvement
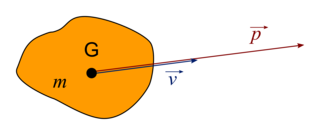 |
Le vecteur quantité de mouvement 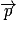 d'un système donné est défini par le produit de sa masse m et de sa vitesse
d'un système donné est défini par le produit de sa masse m et de sa vitesse 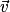 . On a
. On a 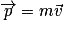 , avec m en kg, v en
, avec m en kg, v en 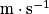 et p en
et p en 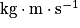 .
.
Plus la valeur de p est grande, plus le corps en mouvement a tendance à « continuer sur sa lancée » (c'est-à-dire à continuer son mouvement dans la même direction). Par exemple, une balle plus lourde et/ou allant plus vite sera plus difficile à arrêter qu'une balle moins lourde et/ou allant moins vite.
La quantité de mouvement d'un système constitué de plusieurs éléments est la somme vectorielle des quantités de mouvement des solides qui constituent le système.
Exemple : Dans une fusée qui décolle, la quantité de mouvement du système {fusée + carburant} se conserve : la fusée s'envole vers le haut alors que le carburant est éjecté vers le bas.
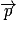 d'un système donné est défini par le produit de sa masse m et de sa vitesse
d'un système donné est défini par le produit de sa masse m et de sa vitesse 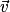 . On a
. On a 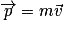 , avec m en kg, v en
, avec m en kg, v en 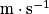 et p en
et p en 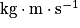 .
.Plus la valeur de p est grande, plus le corps en mouvement a tendance à « continuer sur sa lancée » (c'est-à-dire à continuer son mouvement dans la même direction). Par exemple, une balle plus lourde et/ou allant plus vite sera plus difficile à arrêter qu'une balle moins lourde et/ou allant moins vite.
La quantité de mouvement d'un système constitué de plusieurs éléments est la somme vectorielle des quantités de mouvement des solides qui constituent le système.
Exemple : Dans une fusée qui décolle, la quantité de mouvement du système {fusée + carburant} se conserve : la fusée s'envole vers le haut alors que le carburant est éjecté vers le bas.
Zoom sur…
L'utilisation de la force électrostatique : principe simplifié des accélérateurs linéaires de particules
Dans un accélérateur linéaire de particules, on accélère des particules chargées en les plaçant dans un champ électrique uniforme. Pour cela, on applique entre deux armatures métalliques A et B séparés par une distance d une tension U.Rappel : entre deux armatures A et B (comme dans un condensateur plan), le champ électrique
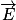 est uniforme, dirigé de l'armature positive vers l'armature négative, ou dirigé vers les potentiels décroissants.
est uniforme, dirigé de l'armature positive vers l'armature négative, ou dirigé vers les potentiels décroissants.De plus, l'intensité du champ électrique est telle que :
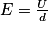 , avec E en
, avec E en 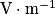 , U la tension entre les bornes du condensateur plan en V, et d la distance entre les armatures en m.
, U la tension entre les bornes du condensateur plan en V, et d la distance entre les armatures en m.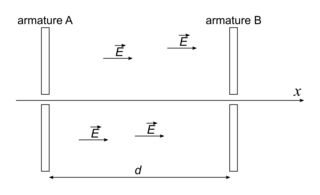 |
Ainsi, les particules passant par le dispositif peuvent atteindre des vitesses et donc des énergies très élevées, ce qui facilite leur interaction avec la matière. Cela peut notamment permettre de générer des rayons X, utilisés dans de nombreux domaines comme la médecine ou l'industrie.
Un exemple célèbre est celui de l'Accélérateur Grand Louvre d'Analyse Élémentaire (AGLAE), qui utilise ce procédé afin d'identifier les pigments recouvrant les œuvres.
Un exemple célèbre est celui de l'Accélérateur Grand Louvre d'Analyse Élémentaire (AGLAE), qui utilise ce procédé afin d'identifier les pigments recouvrant les œuvres.

