Modéliser l'écoulement d'un fluide (non évaluable à l'épreuve écrite)
La mécanique des fluides est un domaine de la physique consacré à l'étude du comportement des fluides et des interactions qui leur sont associées. On définit comme fluide (liquide ou gaz) un ensemble de particules microscopiques qui s'adapte à ce qui le contient (récipient, tuyau, lit d'une rivière, etc.). Cela concerne notamment les liquides comme l'eau, ou les gaz comme l'air.
I. Comment décrire un fluide au repos par la poussée d'Archimède ?
On considère un objet plongé dans un fluide. La pression au sein du fluide n'est pas uniforme, car elle dépend de la profondeur. Cette variation de pression le long de l'objet que l'on immerge le pousse vers la surface. C'est ce qu'on appelle la « poussée d'Archimède ».Ainsi, la poussée d'Archimède correspond à la résultante des forces pressantes exercées par un fluide, en équilibre dans le champ de pesanteur, sur un corps entièrement immergé dans ce fluide.
Elle s'écrit de la façon suivante PArchimède = Vdéplacé × μfluide × g, avec
• Vdéplacé, le volume de fluide déplacé par l'objet en m3 ;
• μfluide, la masse volumique du fluide en 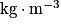 ;
;
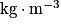 ;
;• g, la constante de pesanteur terrestre en 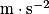 .
.
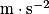 .
.De façon plus imagée, on peut dire que la valeur de la poussée d'Archimède correspond au poids du fluide que l'objet a remplacé lorsqu'il a été immergé.
Le vecteur est orienté de façon opposée au vecteur poids
est orienté de façon opposée au vecteur poids 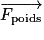 .
.
Exemple : lorsque l'on place un glaçon au fond d'un verre d'eau, il aura tendance à remonter à la surface. En effet, la masse volumique du glaçon est plus petite que celle de l'eau liquide. Cela veut dire que la valeur de la poussée d'Archimède est plus élevée que le poids du glaçon. Celle-ci étant opposée au poids, elle pousse le glaçon vers la surface.
Le vecteur
 est orienté de façon opposée au vecteur poids
est orienté de façon opposée au vecteur poids 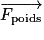 .
.Exemple : lorsque l'on place un glaçon au fond d'un verre d'eau, il aura tendance à remonter à la surface. En effet, la masse volumique du glaçon est plus petite que celle de l'eau liquide. Cela veut dire que la valeur de la poussée d'Archimède est plus élevée que le poids du glaçon. Celle-ci étant opposée au poids, elle pousse le glaçon vers la surface.
II. Comment étudier l'écoulement d'un fluide en régime permanent ?
On étudie ici l'écoulement d'un fluide, comme celui de l'eau le long d'une rivière ou à l'intérieur d'un tuyau.Faisons quelques hypothèses sur les écoulements de fluides étudiés ici :
• le régime d'écoulement est dit permanent ou stationnaire, ce qui signifie que les grandeurs qui le caractérisent (vitesse, pression, masse volumique, température, etc.) ne varient pas dans le temps ;
• les fluides considérés sont dits incompressibles : leur volume ne dépend pas de la pression ; leur masse volumique est donc constante le long de l'écoulement.
III. Qu'est-ce que le concept de débit ?
Le débit volumique Qv d'un fluide correspond au volume de fluide traversant une section S par unité de temps Δt. On a :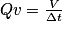 , avec Qv en
, avec Qv en 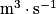 , V en m3, Δt en s.
, V en m3, Δt en s.De même, le débit massique Qm d'un fluide correspond à la masse de fluide traversant une section S par unité de temps Δt.
Ces deux débits sont reliés par la formule suivante :
Qm = μfluide × Qv, avec μfluide en
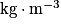 , Qm en
, Qm en 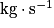 .
.On peut également déduire la vitesse d'écoulement du fluide vfluide à partir du débit volumique Qv et de la section S par laquelle passe le fluide. Ainsi, on a :
Qv = vfluide × S.
Exemple :
Un robinet parvient à remplir une bouteille d'eau d'un litre en 10 s.
Ainsi, le débit volumique de l'eau au travers du robinet est :
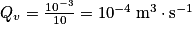 .
.La masse volumique de l'eau étant de
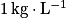 , soit
, soit 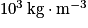 , on en déduit le débit massique de l'écoulement :
, on en déduit le débit massique de l'écoulement :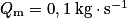 .
.Enfin, sachant que le robinet a une section S = 1cm2 = 10−4 m2, on en déduit la vitesse d'écoulement de l'eau dans la bouteille :
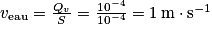 .
.IV. Quel est le rapport entre débit et conservation de la matière ?
La conservation de la matière permet, dans un écoulement fluide, la conservation du débit massique Qm.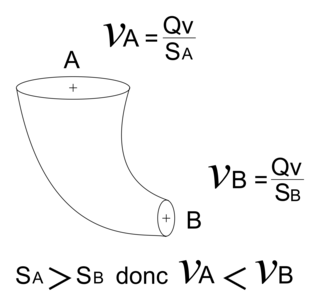 |
Le fluide étant considéré comme incompressible, sa masse volumique ne varie pas et il y a donc aussi conservation du débit volumique Qv. On en déduit ainsi les variations de vitesse du fluide en fonction de la variation de la taille S d'écoulement.
V. Qu'est-ce qu'un tube de courant ?
En régime stationnaire, la courbe le long de laquelle se déplace un élément fluide est appelée ligne de courant. Le vecteur vitesse en chaque point du fluide est tangent à la ligne de courant qui passe par celui-ci. Concrètement, cela correspond au « chemin » parcouru par la particule de fluide dans l'écoulement.On appelle tube de courant un ensemble de lignes de courant s'appuyant sur une courbe fermée. Un tuyau ou un robinet rempli entièrement est un exemple de tube de courant.
VI. Qu'est-ce que la relation de Bernoulli pour un fluide parfait incompressible ?
On considère, dans cette partie, que le fluide étudié est parfait, c'est-à-dire qu'il s'écoule sans frottement et qu'il est incompressible. On travaille toujours en régime permanent.Dans ces conditions, la relation de Bernoulli permet de relier la vitesse d'un fluide, sa pression et son altitude le long d'une ligne de courant ou d'un tube de courant de l'écoulement. En effet, entre deux points A et B le long d'un écoulement dans une section fermée, la relation de Bernoulli s'écrit de la façon suivante :
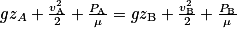 , avec
, avec• μ la masse volumique du fluide en 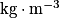 ;
;
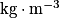 ;
;• vA et vB les vitesses du fluide aux points A et B en 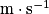 ;
;
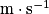 ;
;• PA et PB les pressions du fluide aux points A et B en Pa ;
• zA et zB les hauteurs des points A et B considérés, en m ;
• g la constante de pesanteur terrestre en 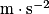 .
.
Cette relation traduit la conservation de l'énergie mécanique au sein d'un écoulement fluide.
Remarque : en pratique, on assimilera très souvent l'ensemble de l'écoulement à un tube de courant pour pouvoir appliquer la relation de Bernoulli directement.
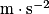 .
.Cette relation traduit la conservation de l'énergie mécanique au sein d'un écoulement fluide.
Remarque : en pratique, on assimilera très souvent l'ensemble de l'écoulement à un tube de courant pour pouvoir appliquer la relation de Bernoulli directement.
VII. Qu'est-ce que l'effet Venturi ?
L'effet Venturi correspond à un phénomène de mécanique des fluides traduisant le principe de conservation de la masse, où l'on observe qu'une accélération de particules fluides dans une zone induit une baisse de la pression. Par exemple, les rapides d'une rivière ou l'accélération du vent dans un col de montagne témoignent de cet effet.Ce phénomène peut être compris à l'aide de la relation de Bernoulli. Pour cela, considérons une conduite horizontale, dont la section en entrée SA est rétrécie au point B où sa section est SB. Le débit volumique Qv est le même le long de la conduite. On peut représenter le problème de la façon suivante :
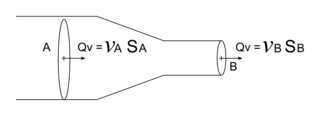 |
Dans cette situation, la hauteur ne varie pas, car la conduite est horizontale. Ainsi, la relation de Bernoulli entre l'entrée A et la sortie B s'écrit de la façon suivante :
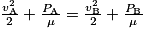 .
.
De plus, on sait que le débit Qv est le même le long de la conduite. On a donc en entrée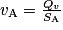 , et en sortie
, et en sortie 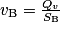 .
.
Comme SA > SB, on remarque que vA < vB, ce qui correspond à l'une des manifestations de l'effet Venturi.
En remplaçant vA et vB par leurs expressions dans la relation de Bernoulli, on obtient :
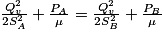 .
.
En mettant les termes PA et PB du même côté et en multipliant par μ, on obtient l'expression suivante :
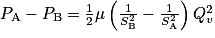 .
.
Comme SA > SB,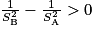 , et PA − PB > 0.
, et PA − PB > 0.
Cela signifie qu'il y a une dépression du fluide lorsque la conduite est rétrécie. C'est l'autre manifestation notable de l'effet Venturi.
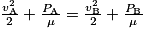 .
.De plus, on sait que le débit Qv est le même le long de la conduite. On a donc en entrée
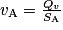 , et en sortie
, et en sortie 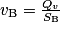 .
.Comme SA > SB, on remarque que vA < vB, ce qui correspond à l'une des manifestations de l'effet Venturi.
En remplaçant vA et vB par leurs expressions dans la relation de Bernoulli, on obtient :
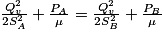 .
.En mettant les termes PA et PB du même côté et en multipliant par μ, on obtient l'expression suivante :
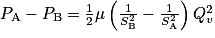 .
.Comme SA > SB,
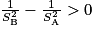 , et PA − PB > 0.
, et PA − PB > 0.Cela signifie qu'il y a une dépression du fluide lorsque la conduite est rétrécie. C'est l'autre manifestation notable de l'effet Venturi.
Zoom sur…
Un concept-clé, la pression
La pression est une grandeur physique qui traduit les échanges de quantité de mouvement dans la matière, et notamment au sein d'un fluide ou d'un solide. Elle correspond à l'intensité d'une force rapportée à la surface sur laquelle elle s'applique.Ainsi, pour une force F appliquée à une surface S, la pression s'écrit :
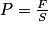 .
.L'unité de mesure du système international de la pression est le pascal (Pa). Une autre unité de mesure est le bar, correspondant à 105 Pa. C'est cette unité qui est le plus souvent utilisée dans la vie courante.
La pression est fondamentale pour caractériser un fluide, puisqu'elle entre en relation avec d'autres grandeurs, telles que la température, la masse volumique ou le mouvement, comme on le verra avec la relation de Bernoulli.
Exemple : la pression atmosphérique vaut environ 105 Pa, soit 1 bar. La pression relative d'un pneu de voiture par rapport à l'atmosphère est de 2,5 bar, ce qui correspond à une pression absolue de 3,5 bar.
La famille Bernoulli
Daniel Bernoulli, qui a pour la première fois énoncé la relation de Bernoulli, n'est pas le seul Bernoulli à avoir marqué l'histoire des sciences. En effet, cette famille de riches commerçants bâlois ne compte pas moins de neuf membres, sur trois générations, ayant contribué à l'histoire de la physique ou des mathématiques, et ce durant toute la seconde moitié du xviie siècle et tout au long du xviiie siècle.On peut par exemple évoquer Jacques et Jean, qui ont tous deux beaucoup travaillé sur le calcul infinitésimal. On doit notamment à Jacques Bernoulli la découverte de la fameuse constante mathématique e, qui est le nombre tel que lne = 1.
Exercice n°1
Une bille de forme sphérique de 10 cm de diamètre est plongée dans un verre d'eau.
Données :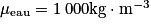 ,
, 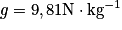 .
.
Pour une boule de rayon R, on calcule son volume V et sa surface S comme suit :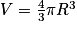 , S = 4πR2.
, S = 4πR2.
Quelle est la valeur de la poussée d'Archimède qui s'exerce sur la bille ?
Données :
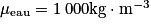 ,
, 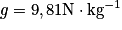 .
.Pour une boule de rayon R, on calcule son volume V et sa surface S comme suit :
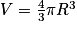 , S = 4πR2.
, S = 4πR2.Quelle est la valeur de la poussée d'Archimède qui s'exerce sur la bille ?
Cochez la bonne réponse.
| ||
| ||
|
On commence par calculer le rayon de la bille 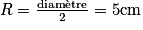 . On calcule ensuite le volume de la bille :
. On calcule ensuite le volume de la bille : 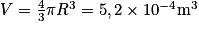 . Enfin, on applique la formule de la poussée d'Archimède : PArchimède = Vdéplacé × μfluide × g = 5,1 N.
. Enfin, on applique la formule de la poussée d'Archimède : PArchimède = Vdéplacé × μfluide × g = 5,1 N.
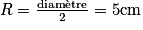 . On calcule ensuite le volume de la bille :
. On calcule ensuite le volume de la bille : 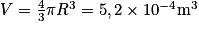 . Enfin, on applique la formule de la poussée d'Archimède : PArchimède = Vdéplacé × μfluide × g = 5,1 N.
. Enfin, on applique la formule de la poussée d'Archimède : PArchimède = Vdéplacé × μfluide × g = 5,1 N.Exercice n°2
Combien vaut la pression résultante associée à la poussée d'Archimède s'appliquant sur la bille de la question précédente ?
Cochez la bonne réponse.
| ||
| ||
|
On utilise la réponse à la question précédente pour appliquer la formule de la pression sur la poussée d'Archimède sur la bille de surface S et de rayon R :
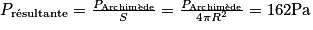 .
.
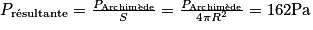 .
.Exercice n°3
Un fluide s'écoule dans une conduite avec un débit massique 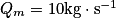 . Quelle masse aura traversé la conduite au bout de 20 secondes ?
. Quelle masse aura traversé la conduite au bout de 20 secondes ?
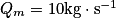 . Quelle masse aura traversé la conduite au bout de 20 secondes ?
. Quelle masse aura traversé la conduite au bout de 20 secondes ? Cochez la bonne réponse.
| ||
| ||
|
En utilisant la formule du débit massique, on trouve que la masse m traversant la conduite en 20 s vaut : m = Qm × Δt = 10 × 20 = 200 kg.

