Énoncé
Exercice sur 4 points
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Justifier chaque réponse. Une réponse non justifiée ne rapporte aucun point.
1. La suite (un) est définie pour tout entier naturel n par :
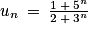
Affirmation 1 : La suite (un) converge vers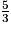 .
.
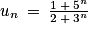
Affirmation 1 : La suite (un) converge vers
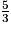 .
.2. On considère la suite (wn) définie par :
w0 = 0 et, pour tout entier naturel n, wn+1=3wn − 2n + 3.
Affirmation 2 : Pour tout entier naturel n, wn ≥ n.
w0 = 0 et, pour tout entier naturel n, wn+1=3wn − 2n + 3.
Affirmation 2 : Pour tout entier naturel n, wn ≥ n.
3. On considère la fonction f définie sur ![\left ]0\: ;\: +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde38_m3.png) , dont la courbe représentative Cf est donnée dans un repère orthonormé sur la figure (fig. 1) en page 5. On précise que :
, dont la courbe représentative Cf est donnée dans un repère orthonormé sur la figure (fig. 1) en page 5. On précise que :
![\left ]0\: ;\: +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde38_m3.png) , dont la courbe représentative Cf est donnée dans un repère orthonormé sur la figure (fig. 1) en page 5. On précise que :
, dont la courbe représentative Cf est donnée dans un repère orthonormé sur la figure (fig. 1) en page 5. On précise que :• T est la tangente à Cf au point A d’abscisse 8 ;
• l’axe des abscisses est la tangente horizontale à Cf au point d’abscisse 1.
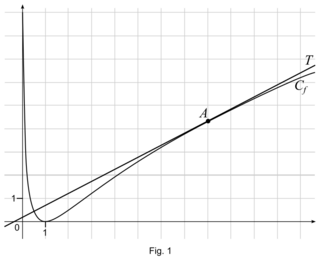 |
Affirmation 3 : D’après le graphique, la fonction f est convexe sur son ensemble de définition.
4. Affirmation 4 : Pour tout réel x > 0, ln(x) − x + 1 ≤ 0, où ln désigne la fonction logarithme népérien.
Corrigé
Affirmation 1
L’étude directe de la limite conduit à une forme indéterminée du type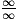 .
.En effet, on sait que pour tout réel q tel que q > 1, on a :
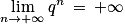
Ainsi :
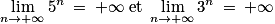
On doit donc transformer l’expression de un afin de lever l’indétermination. Une astuce classique lors d’une forme indéterminée de ce type consiste à factoriser le numérateur et le dénominateur par même facteur. Ici, on peut par exemple factoriser par 3n.
Pour tout n de
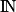 :
: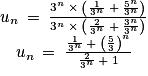
On a :
• 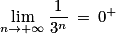 (par quotient) ;
(par quotient) ;
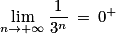 (par quotient) ;
(par quotient) ;• 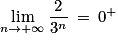 (par quotient) ;
(par quotient) ;
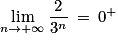 (par quotient) ;
(par quotient) ;• 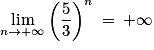 , car
, car 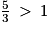 .
.
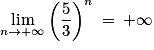 , car
, car 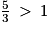 .
.Ainsi, par somme :
• 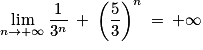
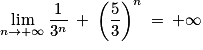
• 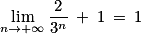
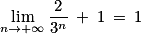
Ainsi, comme 1 > 0, par quotient :
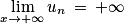
Donc la suite (un) diverge vers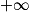 .
.
L’affirmation 1 est donc fausse.
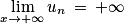
Donc la suite (un) diverge vers
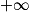 .
.L’affirmation 1 est donc fausse.
Affirmation 2
Les premiers termes semblent confirmer que la propriété est vraie, mais il faut le prouver de manière générale. On va alors utiliser un raisonnement par récurrence car une preuve directe (par inégalités successives) semble compliquée.Soit Pn : "wn ≥ n", pour
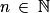 .
.Initialisation : on montre que P0 est vraie.
Pour n = 0, w0 = 0 ≥ 0, donc P0 est vraie.
Hérédité : Soit k un entier naturel. Supposons que Pk est vraie, c’est à dire que wk ≥ k (hypothèse de récurrence). Montrons que Pk+1 est vraie, c’est à dire que wk+1 ≥ k + 1.
On sait que
wk+1 = 3wk − 2k + 3
On part de :
wk ≥ k
3wk ≥ 3k, car 3 > 0
3wk − 2k + 3 ≥ 3k − 2k + 3
wk+1 ≥ k + 3 ≥ k + 1
Donc :
wk+1 ≥ k + 1
Ainsi, Pk+1 est vraie.
On peut conclure que pour tout entier naturel n, wn ≥ n.
Ainsi l’affirmation 2 est vraie.
Affirmation 3
 |
Une fonction est convexe sur son ensemble de définition si et seulement si sa représentation graphique est située au-dessus de toutes ses tangentes. Or, sur [1 ; 8] par exemple, Cf est en dessous de sa tangente T. Donc f n’est pas convexe sur son ensemble de définition. L’affirmation 3 est fausse.
Affirmation 4
Soit T la tangente à la courbe représentative de la fonction ln au point d’abscisse 1.On a :
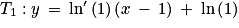
Donc :
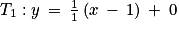
T1:y = x − 1
La fonction ln est concave, car sa dérivée seconde
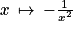 est strictement négative sur
est strictement négative sur ![\left ]0\: ;\: +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde38_m20.png) .
.Donc sa représentation graphique est située en dessous de sa tangente.
Par conséquent, la représentation graphique de la fonction ln est située en dessous de T.
Donc pour tout x > 0, on a ln(x) ≤ x − 1, c’est-à-dire ln(x) − x + 1 ≤ 0.
Donc l’affirmation 4 est vraie.

