Sujet national, juin 2025, exercice 3
Énoncé
Exercice sur 4 points
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Justifier chaque réponse. Une réponse non justifiée ne rapporte aucun point.
1. La suite (un) est définie pour tout entier naturel n par :
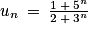
Affirmation 1 : La suite (un) converge vers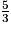 .
.
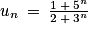
Affirmation 1 : La suite (un) converge vers
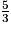 .
.2. On considère la suite (wn) définie par :
w0 = 0 et, pour tout entier naturel n, wn+1=3wn − 2n + 3.
Affirmation 2 : Pour tout entier naturel n, wn ≥ n.
w0 = 0 et, pour tout entier naturel n, wn+1=3wn − 2n + 3.
Affirmation 2 : Pour tout entier naturel n, wn ≥ n.
3. On considère la fonction f définie sur ![\left ]0\: ;\: +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde38_m3.png) , dont la courbe représentative Cf est donnée dans un repère orthonormé sur la figure (fig. 1) en page 5. On précise que :
, dont la courbe représentative Cf est donnée dans un repère orthonormé sur la figure (fig. 1) en page 5. On précise que :
![\left ]0\: ;\: +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde38_m3.png) , dont la courbe représentative Cf est donnée dans un repère orthonormé sur la figure (fig. 1) en page 5. On précise que :
, dont la courbe représentative Cf est donnée dans un repère orthonormé sur la figure (fig. 1) en page 5. On précise que :• T est la tangente à Cf au point A d’abscisse 8 ;
• l’axe des abscisses est la tangente horizontale à Cf au point d’abscisse 1.
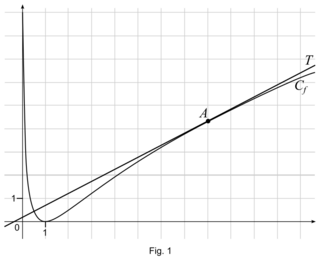 |
Affirmation 3 : D’après le graphique, la fonction f est convexe sur son ensemble de définition.
4. Affirmation 4 : Pour tout réel x > 0, ln(x) − x + 1 ≤ 0, où ln désigne la fonction logarithme népérien.
Annexes
© 2000-2026, Miscellane
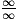 .
.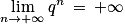
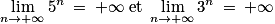
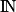 :
: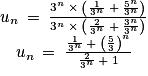
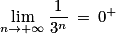 (par quotient) ;
(par quotient) ;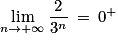 (par quotient) ;
(par quotient) ;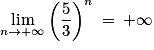 , car
, car 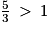 .
.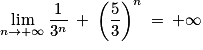
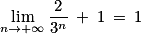
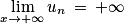
 .
. .
.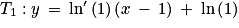
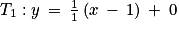
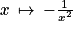 est strictement négative sur
est strictement négative sur ![\left ]0\: ;\: +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde38_m20.png) .
.