Énoncé
Exercice sur 7 points
Partie A : Études des deux fonctions
On considère les deux fonctions f et g définies sur l'intervalle [0 ; +∞[ par :
f(x) = 0,06(−x2 + 13,7x) et g(x) = (− 0,15x + 2,2) e0,2x − 2,2.
On admet que les fonctions f et g sont dérivables et on note f' et g' leurs fonctions dérivées respectives.
f(x) = 0,06(−x2 + 13,7x) et g(x) = (− 0,15x + 2,2) e0,2x − 2,2.
On admet que les fonctions f et g sont dérivables et on note f' et g' leurs fonctions dérivées respectives.
1. On donne le tableau de variations complet de la fonction f sur l'intervalle [0 ; +∞[.
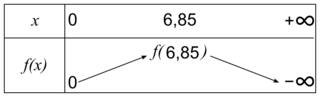 |
1. a. Justifier la limite de f en +∞.
Pour trouver la limite de cette fonction, il faut utiliser la technique usuelle de factorisation par le terme de plus haut degré, sinon c'est une FI.
1. b. Justifier les variations de la fonction f.
C'est une question très classique lors de l'étude d'une fonction. Il faut penser à bien détailler les différentes étapes de la démarche : dérivation de la fonction, puis résolution des inéquations qui permettent d'obtenir le signe de la dérivée et enfin construction du tableau de variations. Il faut également penser à justifier les valeurs remarquables données dans ce tableau.
1. c. Résoudre l'équation f(x) = 0.
Il faut utiliser les méthodes de factorisation et de résolution d'équation produit nul vues au collège pour résoudre cette question rapidement.
2. a. Déterminer la limite de g en +∞.
Pour trouver la limite de cette fonction, il faut utiliser les règles usuelles de limite d'une fonction composée, d'une somme et d'un produit.
2. b. Démontrer que, pour tout réel x appartenant à [0 ; +∞[, on a : g'(x) = (−0,03x + 0,29) e0,2x.
Cette question nécessite l'utilisation de la formule de la dérivée d'un produit et de la dérivée d'une fonction composée. Ce sont des calculs usuels dont il faut détailler chaque étape pour avoir tous les points.
2. c. Étudier les variations de la fonction g et dresser son tableau de variations sur [0 ; +∞[. Préciser une valeur approchée à 10−2 près du maximum de g.
C'est une question très classique lors de l'étude d'une fonction. Il faut penser à bien détailler les différentes étapes de la démarche : dérivation de la fonction, puis résolution des inéquations qui permettent d'obtenir le signe de la dérivée et enfin construction du tableau de variations.
Il faut également penser à justifier les valeurs remarquables données dans ce tableau.
Il faut également penser à justifier les valeurs remarquables données dans ce tableau.
2. d. Montrer que l'équation g(x) = 0 admet une unique solution non nulle et déterminer, à 10−2 près, une valeur approchée de cette solution.
Cette question nécessite l'utilisation du théorème des valeurs intermédiaires. C'est une question très classique et qui est toujours formulée de la même manière lors des études de fonction, il faut donc la reconnaître pour directement se lancer dans le TVI.
Partie B : Trajectoires d'une balle de golf
Pour frapper la balle, un joueur de golf utilise un instrument appelé « club » de golf.
On souhaite exploiter les fonctions f et g étudiées en partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
On admettra ici que 13,7 est la valeur qui annule la fonction f et une approximation de la valeur qui annule la fonction g.
On donne ci-dessous les représentations graphiques de f et g sur l'intervalle [0 ; 13,7].
On souhaite exploiter les fonctions f et g étudiées en partie A pour modéliser de deux façons différentes la trajectoire d'une balle de golf. On suppose que le terrain est parfaitement plat.
On admettra ici que 13,7 est la valeur qui annule la fonction f et une approximation de la valeur qui annule la fonction g.
On donne ci-dessous les représentations graphiques de f et g sur l'intervalle [0 ; 13,7].
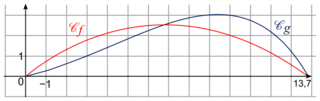 |
Pour x représentant la distance horizontale parcourue par la balle en dizaines de yards après la frappe (avec 0 < x < 13,7), f(x) (ou g(x) selon le modèle) représente la hauteur correspondante de la balle par rapport au sol, en dizaines de yards (1 yard correspond à environ 0,914 mètre).
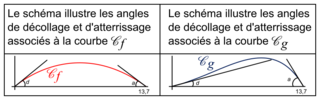
On appelle « angle de décollage » de la balle l'angle entre l'axe des abscisses et la tangente à la courbe (Cf ou Cg selon le modèle) en son point d'abscisse 0. Une mesure de l'angle de décollage de la balle est un nombre réel d tel que tan(d) est égal au coefficient directeur de cette tangente.
De même, on appelle « angle d'atterrissage » de la balle l'angle entre l'axe des abscisses et la tangente à la courbe (Cf ou Cg selon le modèle) en son point d'abscisse 13,7. Une mesure de l'angle d'atterrissage de la balle est un nombre réel a tel que tan(a) est égal à l'opposé du coefficient directeur de cette tangente. Tous les angles sont mesurés en degrés.
On appelle « angle de décollage » de la balle l'angle entre l'axe des abscisses et la tangente à la courbe (Cf ou Cg selon le modèle) en son point d'abscisse 0. Une mesure de l'angle de décollage de la balle est un nombre réel d tel que tan(d) est égal au coefficient directeur de cette tangente.
De même, on appelle « angle d'atterrissage » de la balle l'angle entre l'axe des abscisses et la tangente à la courbe (Cf ou Cg selon le modèle) en son point d'abscisse 13,7. Une mesure de l'angle d'atterrissage de la balle est un nombre réel a tel que tan(a) est égal à l'opposé du coefficient directeur de cette tangente. Tous les angles sont mesurés en degrés.
 |
1. Première modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards, x représente la distance horizontale parcourue par la balle après la frappe et f(x) la hauteur correspondante de la balle. Selon ce modèle :
1. a. Quelle est la hauteur maximale, en yards, atteinte par la balle au cours de sa trajectoire ?
Ici, l'exercice utilise la fonction étudiée en partie A. Il faut donc retrouver la valeur intéressante de cette fonction qui permet de rapidement effectuer le bon calcul pour répondre à cette question.
1. b. Vérifier que f'(0) = 0,822.
Il faut utiliser l'expression de la dérivée de la fonction f déjà étudiée en partie A.
1. c. Donner une mesure en degrés de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
Il faut connaître le lien entre fonction dérivée et coefficient directeur de la tangente à la courbe. Et bien observer que l'angle cherché est relié à cette tangente.
1. d. Quelle propriété graphique de la courbe Cf permet de justifier que les angles de décollage et d'atterrissage de la balle sont égaux ?
Il faut maîtriser le vocabulaire des courbes représentatives et connaître les propriétés des paraboles représentant une fonction du second degré (vues en première) pour répondre.
2. Seconde modélisation : on rappelle qu'ici, l'unité étant la dizaine de yards, x représente la distance horizontale parcourue par la balle après la frappe et g(x) la hauteur correspondante de la balle. Selon ce modèle :
2. a. Quelle est la hauteur maximale, en yards, atteinte par la balle au cours de sa trajectoire ? On précise que g'(0) = 0,29 et g'(13,7) ≈ −1,87.
Il faut utiliser l'expression de la dérivée de la fonction g déjà étudiée en partie A.
2. b. Donner une mesure en degrés de l'angle de décollage de la balle, arrondie au dixième. (On pourra éventuellement utiliser le tableau ci-dessous).
Comme pour la fonction précédente, il faut connaître le lien entre fonction dérivée et coefficient directeur de la tangente à la courbe.
2. c. Justifier que 62 est une valeur approchée, arrondie à l'unité près, d'une mesure en degrés de l'angle d'atterrissage de la balle.
Comme pour la question précédente, il faut connaître le lien entre fonction dérivée et coefficient directeur de la tangente à la courbe, mais au moment de l'atterrissage, et utiliser les valeurs intéressantes de la fonction g dans toutes les questions précédentes.
Tableau : extrait d'une feuille de calcul donnant une mesure en degrés d'un angle quand on connaît sa tangente :
| | A | B | C | D | E | F | G | H | I | J | K | L | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | tan(θ) | 0,815 | 0,816 | 0,817 | 0,818 | 0,819 | 0,82 | 0,821 | 0,822 | 0,823 | 0,824 | 0,825 | 0,826 |
| 2 | θ en degrés | 39,18 | 39,21 | 39,25 | 39,28 | 39,32 | 39,35 | 39,39 | 39,42 | 39,45 | 39,49 | 39,52 | 39,56 |
| 3 | | | | | | | | | | | | | |
| 4 | tan(θ) | 0,285 | 0,286 | 0,287 | 0,288 | 0,289 | 0,29 | 0,291 | 0,292 | 0,293 | 0,294 | 0,295 | 0,296 |
| 5 | θ en degrés | 15,91 | 15,96 | 16,01 | 16,07 | 16,12 | 16,17 | 16,23 | 16,28 | 16,33 | 16,38 | 16,44 | 16,49 |
Partie C : Interrogation des modèles
À partir d'un grand nombre d'observations des performances de joueurs professionnels, on a obtenu les résultats moyens suivants :
| Angle de décollage en degrés | Hauteur maximale en yards | Angle d'atterrissage en degrés | Distance horizontale en yards au point de chute |
|---|---|---|---|
| 24 | 32 | 52 | 137 |
Quel modèle, parmi les deux étudiés précédemment, semble le plus adapté pour décrire la frappe de la balle par un joueur professionnel ? La réponse sera justifiée.
Il faut comparer chaque critère de ce tableau aux valeurs obtenues avec les deux modèles représentés par les fonctions f et g. Il faut ici faire attention à la rédaction de chaque vérification pour conclure sans omettre aucune justification.
Corrigé
Partie A : Études des deux fonctions
1. a. En factorisant l'expression, on a 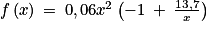 .
.
On a alors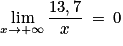 , donc
, donc 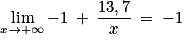 et par produit de limites
et par produit de limites 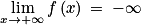 .
.
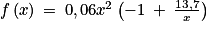 .
.On a alors
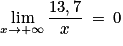 , donc
, donc 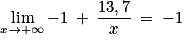 et par produit de limites
et par produit de limites 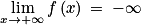 .
.1. b. La fonction polynomiale f est dérivable sur  et sur cet intervalle, on obtient la dérivée : f'(x) = 0,06 × (−2x) + 0,06 × 13,7 = 0,822 − 0,12x.
et sur cet intervalle, on obtient la dérivée : f'(x) = 0,06 × (−2x) + 0,06 × 13,7 = 0,822 − 0,12x.
On a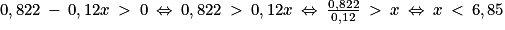 .
.
De même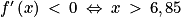 .
.
La fonction f est croissante sur [0 ; 6,85] et décroissante sur [6,85 ; +∞[.
 et sur cet intervalle, on obtient la dérivée : f'(x) = 0,06 × (−2x) + 0,06 × 13,7 = 0,822 − 0,12x.
et sur cet intervalle, on obtient la dérivée : f'(x) = 0,06 × (−2x) + 0,06 × 13,7 = 0,822 − 0,12x.On a
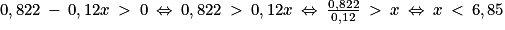 .
.De même
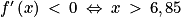 .
.La fonction f est croissante sur [0 ; 6,85] et décroissante sur [6,85 ; +∞[.
1. c. 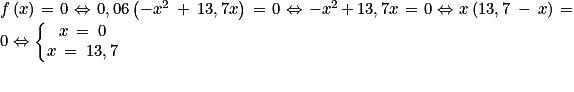 . On a donc l'ensemble des solutions S = {0 ; 13,7}.
. On a donc l'ensemble des solutions S = {0 ; 13,7}.
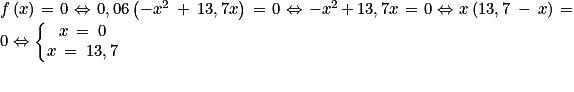 . On a donc l'ensemble des solutions S = {0 ; 13,7}.
. On a donc l'ensemble des solutions S = {0 ; 13,7}.2. a. On a 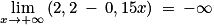 ; d'autre part
; d'autre part 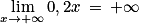 et donc par composition, on a :
et donc par composition, on a : 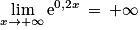 . Ainsi, par produit et somme de limites, on obtient finalement
. Ainsi, par produit et somme de limites, on obtient finalement 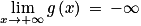 .
.
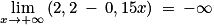 ; d'autre part
; d'autre part 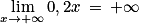 et donc par composition, on a :
et donc par composition, on a : 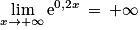 . Ainsi, par produit et somme de limites, on obtient finalement
. Ainsi, par produit et somme de limites, on obtient finalement 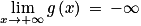 .
.2. b. La fonction g est un produit de fonctions dérivables sur [0 ; +∞[ et sur cet intervalle, on a : g'(x) = −0,15e0,2x + 0,2(−0,15x + 2,2)e0,2x = e0,2x(−0,15 − 0,03x + 0,44) = (−0,03x + 0,29)e0,2x.
2. c. On a donc 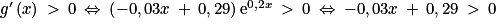 , car e0,2x > 0 quel que soit le réel x. Ainsi, on a
, car e0,2x > 0 quel que soit le réel x. Ainsi, on a 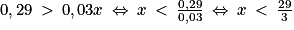 .
.
On obtient de la même façon que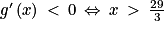 .
.
La fonction g est donc croissante sur![\left [ 0\: ;\: \frac{29}{3}\right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde27_m15.png) ¸ puis décroissante sur
¸ puis décroissante sur 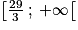 .
.
Une valeur approchée du maximum de g est donc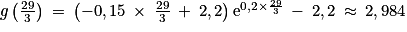 soit 2,98 au centième près.
soit 2,98 au centième près.
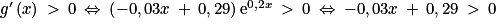 , car e0,2x > 0 quel que soit le réel x. Ainsi, on a
, car e0,2x > 0 quel que soit le réel x. Ainsi, on a 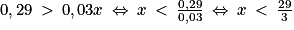 .
.On obtient de la même façon que
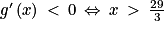 .
.La fonction g est donc croissante sur
![\left [ 0\: ;\: \frac{29}{3}\right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde27_m15.png) ¸ puis décroissante sur
¸ puis décroissante sur 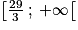 .
.Une valeur approchée du maximum de g est donc
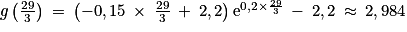 soit 2,98 au centième près.
soit 2,98 au centième près.2. d. La fonction g croit à partir de g(0) = 2,2e0 − 2,2 = 2,2 − 2,2 = 0 jusqu'à environ 2,98 et décroit ensuite jusqu'en moins l'infini.
Sur l'intervalle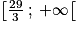 , la fonction g est strictement décroissante et continue, car dérivable sur cet intervalle. De plus, comme
, la fonction g est strictement décroissante et continue, car dérivable sur cet intervalle. De plus, comme ![0\: \in \: \left ] -\infty \: ;\: 2,98\right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde27_m19.png) , il existe donc, d'après le théorème des valeurs intermédiaires, un réel unique α tel que g(α) = 0.
, il existe donc, d'après le théorème des valeurs intermédiaires, un réel unique α tel que g(α) = 0.
Sur l'intervalle
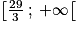 , la fonction g est strictement décroissante et continue, car dérivable sur cet intervalle. De plus, comme
, la fonction g est strictement décroissante et continue, car dérivable sur cet intervalle. De plus, comme ![0\: \in \: \left ] -\infty \: ;\: 2,98\right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde27_m19.png) , il existe donc, d'après le théorème des valeurs intermédiaires, un réel unique α tel que g(α) = 0.
, il existe donc, d'après le théorème des valeurs intermédiaires, un réel unique α tel que g(α) = 0.Partie B : Trajectoires d'une balle de golf
1. a. On a vu que le maximum de f sur [0 ; +∞[ est f(6,85) = 0,06(−6,852 + 13,7 × 6,85) = 2,815 35 ≈ 2,815 soit 28,15 yards.
1. b. Avec l'expression de la dérivée f'(x) = 0,06(−2x + 13,7), on déduit que f'(0) = 0,06 × 13,7 = 0,822. Ce nombre dérivé est le coefficient directeur de la tangente à la courbe Cf au point d'abscisse 0, donc f'(0) = tan d = 0,822.
1. c. D'après le tableau donné (colonne I), on a donc d ≈ 39,42°.
1. d. La courbe est une partie de parabole et celle-ci est symétrique autour de la droite d'équation y = 6,85 : on peut donc en déduire que les angles de décollage et d'atterrissage sont égaux.
2. a. On a vu que le maximum de la fonction g sur l'intervalle [0 ; +∞[ est 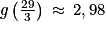 .
.
La hauteur maximale de la balle est donc 29,8 (yards).
On précise que g'(0) = 0,29 et g'(13,7) ≈ −1,87.
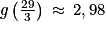 .
.La hauteur maximale de la balle est donc 29,8 (yards).
On précise que g'(0) = 0,29 et g'(13,7) ≈ −1,87.
2. b. On observe que g'(0) = 0,29 et que c'est aussi, comme dans le premier cas, le coefficient directeur de la tangente au point d'abscisse 0, donc tan d ≈ 0,29 et, d'après le tableau, on obtient d ≈ 16,2°.
2. c. On observe par contre qu'à l'atterrissage, on a : g'(13,7) ≈ −1,87 donc tan a ≈ 1,87 d'où a ≈ 61,9°.
Partie C : Interrogation des modèles
Au vu des observations sur les professionnels, on remarque que :
• le seul résultat confirmé est la distance horizontale 137, en yards ;
• l'angle de décollage est surestimé avec la première modélisation et sous-estimé avec la seconde ;
• la hauteur maximale est sous-estimée dans les deux cas ;
• l'angle d'atterrissage est sous-estimé dans le premier cas et surestimé dans le second.
Conclusion : aucun des deux modèles n'est satisfaisant !

