Énoncé
Exercice sur 7 points
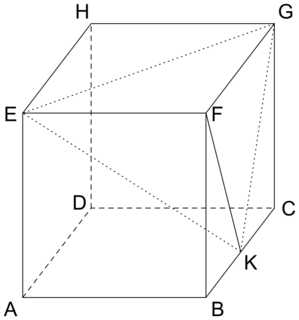
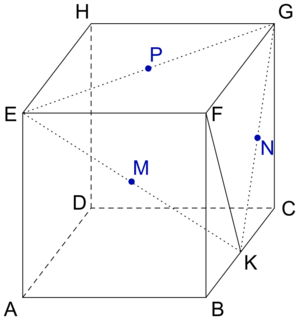
On considère un cube ABCDEFGH et on appelle K le milieu du segment [BC].
 |
On se place dans le repère (A ; 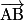 ,
, 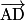 ,
, 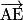 ) et on considère le tétraèdre EFGK.
) et on considère le tétraèdre EFGK.
On rappelle que le volume d'un tétraèdre est donné par :
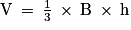
où B désigne l'aire d'une base et h la hauteur relative à cette base.
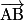 ,
, 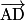 ,
, 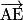 ) et on considère le tétraèdre EFGK.
) et on considère le tétraèdre EFGK.On rappelle que le volume d'un tétraèdre est donné par :
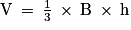
où B désigne l'aire d'une base et h la hauteur relative à cette base.
1. Préciser les coordonnées des points E, F, G et K.
C'est la première question de l'exercice et c'est une question de cours. On cherche à voir si l'élève connaît le lien entre un repère de l'espace et les coordonnées de certains points. Il n'y a pas vraiment de justification attendue à cette question.
2. Montrer que le vecteur 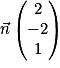 est orthogonal au plan (EGK).
est orthogonal au plan (EGK).
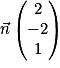 est orthogonal au plan (EGK).
est orthogonal au plan (EGK).Il faut utiliser le lien entre orthogonalité et produit scalaire pour répondre à cette question, en étant vigilant, car on veut montrer l'orthogonalité à un plan (qui est défini par 2 vecteurs).
3. Démontrer que le plan (EGK) admet pour équation cartésienne : 2x − 2y + z − 1 = 0.
C'est une question « classique » dans les exercices de géométrie dans l'espace. Il faut la réaliser étape par étape et bien utiliser les formules du cours et les coordonnées des points et des vecteurs obtenues aux questions 1 et 2.
4. Déterminer une représentation paramétrique de la droite (d) orthogonale au plan (EGK) passant par F.
C'est une question « classique » dans les exercices de géométrie dans l'espace. On cherche à voir si l'élève connaît le lien entre représentation paramétrique et vecteur directeur d'une droite.
5. Montrer que le projeté orthogonal L de F sur le plan (EGK) a pour coordonnées 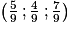 .
.
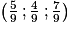 .
.Cette question traite de projection orthogonale, mais ce n'est pas dans cette direction qu'il faut aller, car cela compliquerait le travail. Il faut utiliser le fait que le point H est le point d'intersection de deux objets de l'espace et ainsi résoudre le système paramétrique associé à cette notion d'intersection.
6. Justifier que la longueur LF est égale à 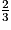 .
.
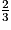 .
.À nouveau, c'est une question « classique » de calcul d'une longueur dans un exercice de géométrie dans l'espace. Il faut donc connaître la formule permettant de calculer la longueur et voir qu'elle nécessite la connaissance des coordonnées du vecteur associé. C'est la première étape de la résolution de cette question.
7. Calculer l'aire du triangle EFG. En déduire que le volume du tétraèdre EFGK est égal à 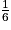 .
.
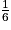 .
.Il faut utiliser ici les formules usuelles de calculs d'aires et de volumes apprises depuis le collège. Il faut penser à bien détailler les calculs et utiliser les valeurs obtenues précédemment dans l'exercice.
8. Déduire des questions précédentes l'aire du triangle EGK.
Il faut penser à bien détailler les calculs et utiliser les valeurs obtenues précédemment dans l'exercice. Il faut pour cela utiliser toutes les formules du cours à sa disposition et ne pas hésiter à isoler les valeurs inconnues dans les équations.
9. On considère les points P milieu du segment [EG], M milieu du segment [EK] et N milieu du segment [GK]. Déterminer le volume du tétraèdre FPMN.
C'est la dernière question du problème. Il faut donc utiliser toutes les questions précédentes pour réaliser cette question. Il manque tout de même quelques valeurs numériques pour conclure, mais elles sont rapides à obtenir. Il ne faut pas hésiter à commencer cette question et avancer au maximum, car chaque étape sera valorisée dans la notation.
Corrigé
1. Les coordonnées des points E, F, G et K.
E(0 ; 0 ; 1), F(1 ; 0 ; 1), G(1 ; 1 ; 1),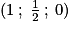 .
.
E(0 ; 0 ; 1), F(1 ; 0 ; 1), G(1 ; 1 ; 1),
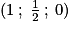 .
.2. D'après la question précédente : 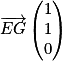 et
et 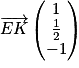 .
.
D'où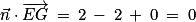 : ces deux vecteurs sont orthogonaux ;
: ces deux vecteurs sont orthogonaux ; 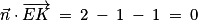 : ces deux vecteurs sont orthogonaux.
: ces deux vecteurs sont orthogonaux.
Le vecteur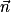 , orthogonal à deux vecteurs non colinéaires du plan (EGK), est orthogonal à ce plan.
, orthogonal à deux vecteurs non colinéaires du plan (EGK), est orthogonal à ce plan.
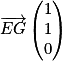 et
et 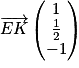 .
.D'où
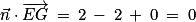 : ces deux vecteurs sont orthogonaux ;
: ces deux vecteurs sont orthogonaux ; 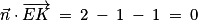 : ces deux vecteurs sont orthogonaux.
: ces deux vecteurs sont orthogonaux.Le vecteur
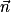 , orthogonal à deux vecteurs non colinéaires du plan (EGK), est orthogonal à ce plan.
, orthogonal à deux vecteurs non colinéaires du plan (EGK), est orthogonal à ce plan.3. Le résultat de la question précédente montre qu'une équation du plan (EGK) est 2x − 2y + z = d, avec 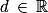 .
.
En particulier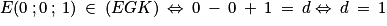 .
.
On a donc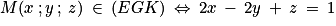 .
.
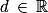 .
.En particulier
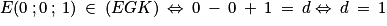 .
.On a donc
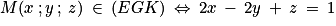 .
.4. La droite (d) étant orthogonale au plan (ECK), on peut prendre comme vecteur directeur de cette droite le vecteur 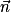 . Elle contient F, donc :
. Elle contient F, donc :
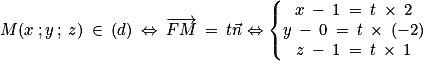 ,
, 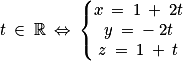 ,
, 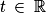 .
.
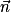 . Elle contient F, donc :
. Elle contient F, donc :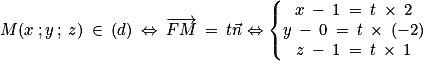 ,
, 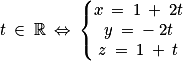 ,
, 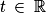 .
.5. L étant le projeté orthogonal de F sur le plan (EGK), L est un point de la droite (d) et du plan (EGK) : ses coordonnées vérifient les équations de (d) et du plan (EGK), donc le système : 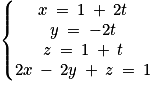 ,
, 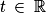 .
.
En remplaçant x, y, et z par leurs expressions en fonction de t dans la dernière équation, on obtient :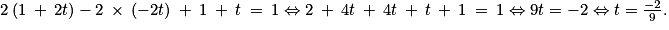
On a donc :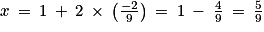 ;
; 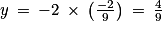 ;
; 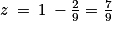 .
.
Conclusion : les coordonnées du point sont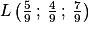 .
.
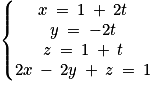 ,
, 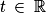 .
.En remplaçant x, y, et z par leurs expressions en fonction de t dans la dernière équation, on obtient :
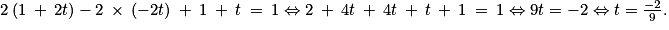
On a donc :
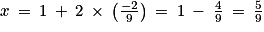 ;
; 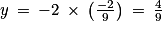 ;
; 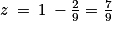 .
.Conclusion : les coordonnées du point sont
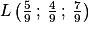 .
.6. Avec les coordonnées du point 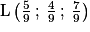 et F(1 ; 0 ; 1), on a
et F(1 ; 0 ; 1), on a 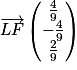 .
.
Donc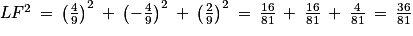 , d'où
, d'où 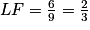 .
.
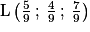 et F(1 ; 0 ; 1), on a
et F(1 ; 0 ; 1), on a 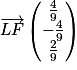 .
.Donc
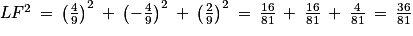 , d'où
, d'où 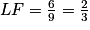 .
.7. Le triangle (EFG) est rectangle en F, donc :
On a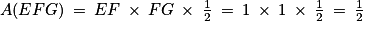 .
.
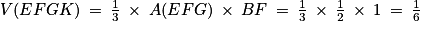 .
.
On a
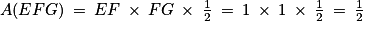 .
.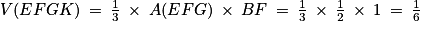 .
.8. On a aussi 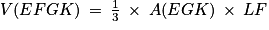 , soit
, soit 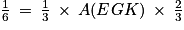 ou encore
ou encore 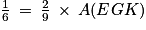 , d'où
, d'où 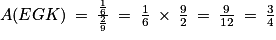 .
.
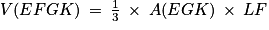 , soit
, soit 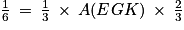 ou encore
ou encore 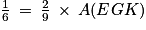 , d'où
, d'où 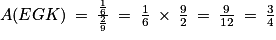 .
.9. D'après le théorème de la droite des milieux, les côtés du triangle (PMN) ont une longueur valant la moitié de celles du triangle (EGK). L'aire du triangle (PMN) est donc égale à 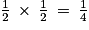 de celle du triangle (EGK), donc
de celle du triangle (EGK), donc 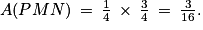
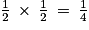 de celle du triangle (EGK), donc
de celle du triangle (EGK), donc 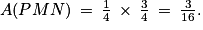
 |
Comme les trois points P, M et N appartiennent au plan (EGK), le triangle (PMN) appartient au plan (EGK) : la hauteur du tétraèdre FPMN est donc la même que celle du tétraèdre (EFGK) soit LF.
On a donc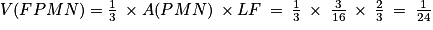 .
.
On a donc
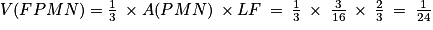 .
.
