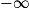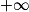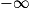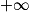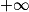Un couple de lapins nés le premier janvier donne naissance à un autre couple de lapins, chaque mois, dès qu'il a atteint l'âge de deux mois. Les nouveaux couples suivent la même loi de reproduction. Combien y aura-t-il de couples de lapins le premier janvier de l'année suivante, en supposant qu'aucun couple n'ait disparu ?
Pour résoudre ce problème, le mathématicien italien Fibonacci introduit dès 1202 la notion de suite.
Ainsi, si on note un le nombre de couples de lapins au cours du mois (avec u1 = 1), la suite (un) vérifie la relation de récurrence un+2 = un+1 + un. On peut alors exprimer un en fonction n de et prévoir le nombre de lapins au bout de quelques mois.
Pour résoudre ce problème, le mathématicien italien Fibonacci introduit dès 1202 la notion de suite.
Ainsi, si on note un le nombre de couples de lapins au cours du mois (avec u1 = 1), la suite (un) vérifie la relation de récurrence un+2 = un+1 + un. On peut alors exprimer un en fonction n de et prévoir le nombre de lapins au bout de quelques mois.
I. Quand utiliser un raisonnement par récurrence et comment le rédiger ?
On peut utiliser un raisonnement par récurrence chaque fois qu'une propriété à démontrer dépend d'un entier naturel n, surtout lorsqu'il semble y avoir un lien simple entre ce qui se passe au rang n et ce qui se passe au rang n+1.
Un raisonnement par récurrence se rédige en quatre étapes :
Un raisonnement par récurrence se rédige en quatre étapes :
• on commence par énoncer la propriété à démontrer, en précisant pour quels entiers naturels cette propriété est définie ;
• initialisation : on vérifie que la propriété est vraie au rang initial (qui est souvent 0 ou 1) ;
• hérédité : on prouve le caractère héréditaire de la propriété. On suppose que la propriété est vraie pour un entier n arbitrairement fixé et on démontre que la propriété est encore vraie au rang n + 1 ;
• on conclut en invoquant le principe de récurrence.
II. Que faut-il savoir sur les suites géométriques ?
Une suite est géométrique quand on passe d'un terme au suivant en multipliant par le même facteur (la raison, notée q).D'où la formule de récurrence donnée pour tout entier n : un+1 = un × q.
Le terme général d'une suite géométrique est : un = u0 × qn.
Enfin la somme des (n + 1) premiers termes d'une suite géométrique (u0 + u1 + … + un) de raison q différente de 1 est égale à :
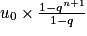 .
.Pour tout réel
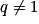 , on a :
, on a : 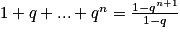 .
.III. Que faut-il savoir sur les suites arithmétiques ?
Une suite est arithmétique quand on passe d'un terme au suivant en ajoutant un même nombre (la raison, notée r).D'où la formule de récurrence donnée pour tout entier n : un+1 = un + r.
Le terme général d'une suite arithmétique est : un = u0 + nr.
Cas particulier : pour tout réel n, on a :
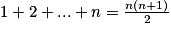 .
.Pour démontrer qu'une suite (un) est arithmétique, on doit calculer un+1 − un et il faut que le résultat obtenu soit un nombre réel indépendant de n.
IV. Comment calculer la limite de qn lorsque q > 0 ?
Trois cas sont possibles :
• premier cas : si 0 < q < 1, alors 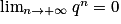 ;
;
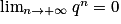 ;
;• deuxième cas : si q = 1, alors 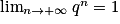 ;
;
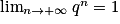 ;
;• troisième cas : si q > 1 alors 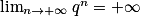 .
.
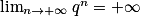 .
.V. Comment déterminer la limite d'une suite ?
Soit (un) une suite géométrique de raison 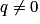 . La limite de la suite (un) dépend de son premier terme u0 non nul et de sa raison q.
. La limite de la suite (un) dépend de son premier terme u0 non nul et de sa raison q.
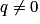 . La limite de la suite (un) dépend de son premier terme u0 non nul et de sa raison q.
. La limite de la suite (un) dépend de son premier terme u0 non nul et de sa raison q.• Pour tout réel u0, si −1 < q < 1, alors 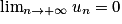 et on dit que (un) converge.
et on dit que (un) converge.
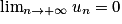 et on dit que (un) converge.
et on dit que (un) converge.• Si u0 > 0 et si q > 1, alors 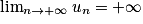 et on dit que (un) diverge.
et on dit que (un) diverge.
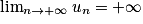 et on dit que (un) diverge.
et on dit que (un) diverge.• Si u0 > et si q < −1, alors alors la suite oscille entre des valeurs positives et négatives de plus en plus grandes. Elle ne converge pas.
• Si u0< 0 et si q > 1, alors 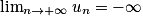 et on dit que (un) diverge.
et on dit que (un) diverge.
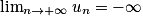 et on dit que (un) diverge.
et on dit que (un) diverge.• Si u0< 0 et si q < −1, alors la suite oscille entre des valeurs positives et négatives de plus en plus grandes. Elle ne converge pas.
Pour étudier la limite d'une suite, on peut exprimer le terme général de la suite en fonction de n et déterminer la limite de ce terme en faisant tendre n vers l'infini.
On peut aussi utiliser les théorèmes de limite par comparaison :
On peut aussi utiliser les théorèmes de limite par comparaison :
• 1er cas : Si un  vn et
vn et 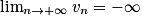 , alors
, alors 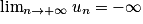 .
.
 vn et
vn et 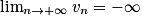 , alors
, alors 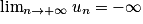 .
.• 2e cas : Si un  vn et
vn et 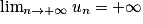 , alors
, alors 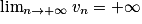 .
.
 vn et
vn et 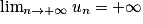 , alors
, alors 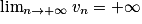 .
.• 3e cas (Théorème des gendarmes) : Si un  wn
wn  vn et
vn et 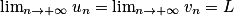 , alors
, alors 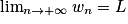 .
.
 wn
wn  vn et
vn et 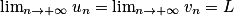 , alors
, alors 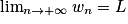 .
.Enfin, on sait que :
• Toute suite croissante majorée est convergente.
• Toute suite décroissante minorée est convergente.
• Une suite est bornée si elle est à la fois majorée et minorée.
VI. Comment calculer la limite de la somme des premiers termes d'une suite géométrique ?
Exemple : Déterminer la limite de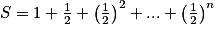 .
.1re étape : On voit la somme des n + 1 premiers termes d'une suite géométrique (un) de premier terme u0 = 1 et de raison
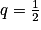 .
.On sait que :
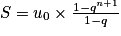 .
.Donc
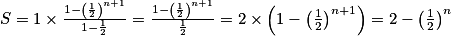 .
.2e étape : Comme
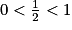 , on a
, on a 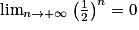 .
.3e étape : Donc
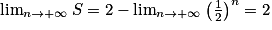 .
.Propriété :
Soit (un) une suite géométrique de premier terme u0 et raison q telle que 0 < q < 1.
Soit S la somme des n + 1 premiers termes de la suite (un). Alors
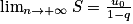 .
.VII. Qu'est-ce qu'une suite arithmético-géométrique ?
Définition : On dit qu'une suite (un) est une suite arithmético-géométrique s'il existe deux réels a et b tels que : u0 étant donné, on a pour tout entier n : un+1 = aun + b.
Exemple : En 2000, la population d'une ville était de 5 200 habitants.
Chaque année, la population augmente de 2 % mais 150 habitants quittent la ville.
On note u0 le nombre d'habitants en 2000, et un le nombre d'habitants en 2000 + n.
Démontrer que la suite (un) est une suite arithmético-géométrique.
On sait qu'une augmentation de 2 % correspond à un coefficient multiplicateur de :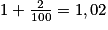 .
.
On a u0 = 5 200 et pour tout entier n : un+1 = 1,02un − 150.
La suite (un) est donc une suite arithmético-géométrique.
Cas particuliers :
Exemple : En 2000, la population d'une ville était de 5 200 habitants.
Chaque année, la population augmente de 2 % mais 150 habitants quittent la ville.
On note u0 le nombre d'habitants en 2000, et un le nombre d'habitants en 2000 + n.
Démontrer que la suite (un) est une suite arithmético-géométrique.
On sait qu'une augmentation de 2 % correspond à un coefficient multiplicateur de :
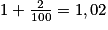 .
.On a u0 = 5 200 et pour tout entier n : un+1 = 1,02un − 150.
La suite (un) est donc une suite arithmético-géométrique.
Cas particuliers :
• Si b = 0 et 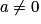 , alors la suite est une suite géométrique de raison a ;
, alors la suite est une suite géométrique de raison a ;
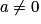 , alors la suite est une suite géométrique de raison a ;
, alors la suite est une suite géométrique de raison a ;• Si a = 1, alors la suite est une suite arithmétique de raison b.
VIII. Algorithmique
Étant donnée une suite (qn) avec 0 < q < 1, on veut élaborer un algorithme permettant de déterminer un seuil à partir duquel qn < a, où a est un réel positif donné.
Déterminer un seuil revient à déterminer le plus petit entier n tel que qn < a.
La condition d'arrêt revient à continuer à calculer qn tant que qn a.
a.
On a donc l'algorithme :
Entrées
Saisir a (nombre réel strictement positif)
Saisir q (nombre réel strictement compris entre 0 et 1)
Initialisation
n prend la valeur 0
Traitement
Tant que : qn a
a
n prend la valeur n + 1
Fin de tant que
Sortie
Afficher n
Déterminer un seuil revient à déterminer le plus petit entier n tel que qn < a.
La condition d'arrêt revient à continuer à calculer qn tant que qn
 a.
a.On a donc l'algorithme :
Entrées
Saisir a (nombre réel strictement positif)
Saisir q (nombre réel strictement compris entre 0 et 1)
Initialisation
n prend la valeur 0
Traitement
Tant que : qn
 a
an prend la valeur n + 1
Fin de tant que
Sortie
Afficher n
 |
Exemple :
Soit la suite (un) définie pour tout entier naturel n par : un = 0,9n.
(un) est strictement décroissante, car 0 < q < 1 et u0 = 0,9.
Pour déterminer le plus petit entier naturel n tel que un < 0,01, on exécute le programme. Dans l'algorithme, on tape seuil (0, 01, 0,9) et on obtient 44.
Soit la suite (un) définie pour tout entier naturel n par : un = 0,9n.
(un) est strictement décroissante, car 0 < q < 1 et u0 = 0,9.
Pour déterminer le plus petit entier naturel n tel que un < 0,01, on exécute le programme. Dans l'algorithme, on tape seuil (0, 01, 0,9) et on obtient 44.
Histoire des mathématiques : suites numériques
• Archimède a défini dans les années 220 av. J.-C. deux suites permettant d'obtenir de très bonnes valeurs approchées de π.
• Héron d'Alexandrie au ier siècle après J.-C. utilise un algorithme de calcul qui fournit une suite de valeurs approchées de plus en plus précises de la racine carrée d'un nombre.
• Léonard de Pise (Fibonacci) expose au xiiie siècle sa célèbre suite.
• Nicolas Oresme, mathématicien français du xive siècle a étudié les suites arithmétiques et géométriques, et la somme des termes de certaines d'entre elles.
• L'idée de fonction est plus récente (xviie siècle). Les mathématiciens ont alors montré qu'une suite est une fonction particulière.
• Augustin Cauchy, mathématicien français du xixe siècle a posé les fondements rigoureux de la théorie des suites.
• La conjecture de Syracuse (xxe siècle) montre une suite avec un comportement particulier, non encore démontré à ce jour.
• Les fractales sont apparues au xixe siècle, et le français Benoit Mandelbrot en fait, dans les années 1970, l'objet d'une nouvelle discipline mathématique : la géométrie fractale.
Zoom sur… les limites des suites
Limite d'une somme
Si 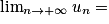 | l | l | l | 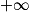 | 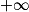 | 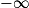 |
Si 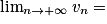 | l' | 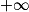 | 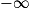 | 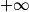 | 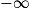 | 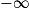 |
Si 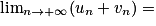 | l + l' | 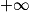 | 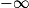 | 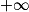 | indéterminée | 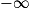 |
Limite d'un produit
Si 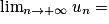 | l | 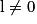 | 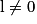 | 0 | 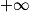 | 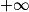 | 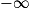 |
Si 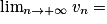 | l' | 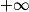 | 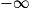 | 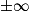 | 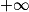 | 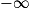 | 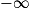 |
Alors 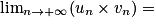 | l × l' | 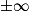 | 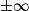 | indéterminée | 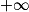 | 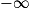 | 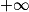 |
Limite d'un inverse
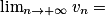 | 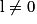 | 0+ | 0− | 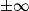 |
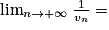 | 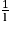 | 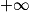 | 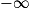 | 0 |
Limite d'un quotient
On a :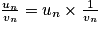 , donc on revient à la règle du produit.
, donc on revient à la règle du produit.Théorème de limites par comparaison
• Si un  vn et
vn et 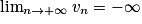 , alors
, alors 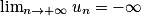 .
.
 vn et
vn et 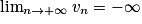 , alors
, alors 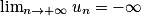 .
.• Si un  vn et
vn et 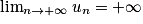 , alors
, alors 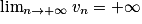 .
.
 vn et
vn et 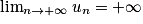 , alors
, alors 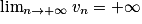 .
.Théorème des gendarmes
Si un wn
wn  vn et
vn et 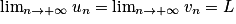 alors
alors 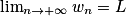 .
.Exercice n°1Exercice n°2Exercice n°3Exercice n°4Exercice n°5Exercice n°6
Exercice n°1
Pour tout entier n supérieur ou égal à 2 on a : 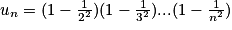
Quelle affirmation est correcte ?
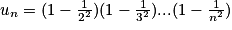
Quelle affirmation est correcte ?
Cochez la bonne réponse.
| ||
| ||
|
Pour n  2, on note Pn la proposition :
2, on note Pn la proposition : 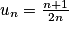 .
.
Initialisation : pour n = 2 on a :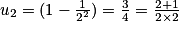 .
.
La proposition est donc vraie au rang n = 2.
Hérédité : on suppose qu'au rang n on a :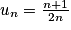 .
.
Au rang (n+1) on aura :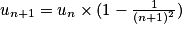 .
.
D'où :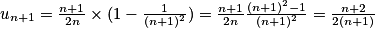 .
.
La proposition est héréditaire.
Donc : pour tout entier n 2,
2, 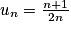 .
.
 2, on note Pn la proposition :
2, on note Pn la proposition : 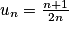 .
.Initialisation : pour n = 2 on a :
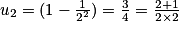 .
.La proposition est donc vraie au rang n = 2.
Hérédité : on suppose qu'au rang n on a :
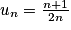 .
.Au rang (n+1) on aura :
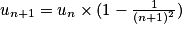 .
.D'où :
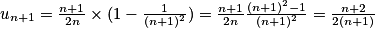 .
. La proposition est héréditaire.
Donc : pour tout entier n
 2,
2, 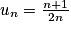 .
.Exercice n°2
Pour tout entier n, on définit la suite (un) par : un = 2 si n est pair et un = − 2 si n est impair.
La suite (un) est-elle une suite géométrique ?
La suite (un) est-elle une suite géométrique ?
Cochez la bonne réponse.
| ||
|
Il y a deux cas :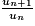 est égal à −1, donc la suite (un) est une suite géométrique de raison −1.
est égal à −1, donc la suite (un) est une suite géométrique de raison −1.
- si n est pair alors un = 2, et n+1 est impair alors un+1 = −2. D'où
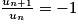 ;
; - si n est impair alors un = −2, et n+1 est pair alors un+1 = 2. D'où
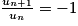 .
.
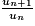 est égal à −1, donc la suite (un) est une suite géométrique de raison −1.
est égal à −1, donc la suite (un) est une suite géométrique de raison −1.Exercice n°3
À quoi est égal : 1 + 2 + 4 +… + 2n ?
Cochez la bonne réponse.
| ||
| ||
|
La somme : 1 + 2 + 4 +… + 2nest de la forme 1 + q + q2 +… + qn avec q = 2.
On sait d'après le cours que :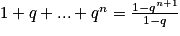 .
.
Donc :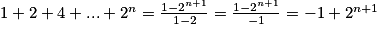 .
.
Par conséquent : 1 + 2 + 4 +… + 2n = 2n+1− 1.
On sait d'après le cours que :
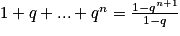 .
.Donc :
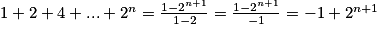 .
.Par conséquent : 1 + 2 + 4 +… + 2n = 2n+1− 1.
Exercice n°4
Quelle est la limite de la suite (un) définie pour tout n par : 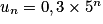 ?
?
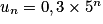 ?
? Cochez la bonne réponse.
| ||
| ||
|
D'après l'expression de la suite (un), on reconnaît une suite géométrique de premier terme 0,3 et de raison q = 5. La raison est strictement supérieure à 1 et le premier terme est positif donc : 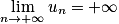 .
.
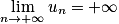 .
.Exercice n°5
Quelle est la limite de la suite (un) définie pour tout n par : 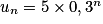 ?
?
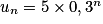 ?
? Cochez la bonne réponse.
| ||
| ||
|
D'après l'expression de la suite (un), on reconnaît une suite géométrique de premier terme 5 et de raison q = 0,3. La raison est strictement comprise entre 0 et 1.
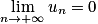
Remarque : le signe du premier terme n'a pas d'importance dans ce cas.
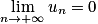
Remarque : le signe du premier terme n'a pas d'importance dans ce cas.
Exercice n°6
À quoi est égale la limite de 0,3n lorsque n tend vers 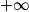 ?
?
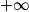 ?
? Cochez la bonne réponse.
| ||
| ||
|
La limite à calculer est de la forme qn avec q = 0,3 strictement compris entre 0 et 1.
D'après le cours on est dans le cas 1 donc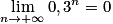
D'après le cours on est dans le cas 1 donc
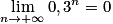
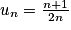 .
.