- Pour encadrer une fraction par deux entiers consécutifs, on peut utiliser la décomposition d'une fraction comme somme d'un entier et d'une fraction strictement inférieure à 1, si on la connaît.
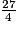 = 6 +
= 6 + 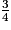 avec
avec 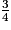 < 1, donc l'encadrement de
< 1, donc l'encadrement de 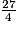 par deux entiers consécutifs est :
par deux entiers consécutifs est :6 <
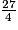 < 7.
< 7.- On peut encadrer le numérateur de la fraction par des multiples du dénominateur.
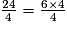 <
< 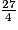 <
< 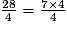 .
.L'encadrement de la fraction
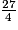 par deux entiers consécutifs est donc : 6 <
par deux entiers consécutifs est donc : 6 < 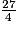 < 7.
< 7.Exercice n°1
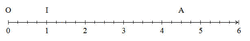 |
Sur la demi-droite graduée ci-dessus, on donne le point A d'abscisse fractionnaire 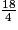 .
.
Encadrez la fraction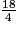 par deux entiers consécutifs.
par deux entiers consécutifs.
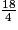 .
.Encadrez la fraction
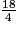 par deux entiers consécutifs.
par deux entiers consécutifs. Écrivez les réponses dans les zones colorées.
On a : < 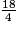 <
<
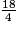 <
< D'après la position du point A d'abscisse fractionnaire 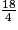 sur la demi-droite graduée, on a : 4 <
sur la demi-droite graduée, on a : 4 < 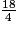 < 5.
< 5.
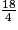 sur la demi-droite graduée, on a : 4 <
sur la demi-droite graduée, on a : 4 < 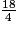 < 5.
< 5.Exercice n°2
Encadrez la fraction 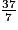 par deux entiers consécutifs.
par deux entiers consécutifs.
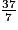 par deux entiers consécutifs.
par deux entiers consécutifs. Écrivez les réponses dans les zones colorées.
On a : < 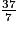 <
<
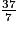 <
< 7×5 = 35 < 37 < 7 × 6 = 42 donc 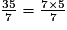 <
< 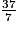 <
< 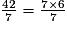 .
.
L'encadrement de la fraction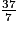 par deux entiers consécutifs est donc : 5 <
par deux entiers consécutifs est donc : 5 < 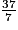 < 6.
< 6.
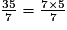 <
< 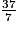 <
< 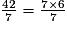 .
.L'encadrement de la fraction
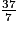 par deux entiers consécutifs est donc : 5 <
par deux entiers consécutifs est donc : 5 < 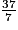 < 6.
< 6.Exercice n°3
L'écriture de la fraction 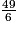 comme somme d'un entier et d'une fraction inférieure à 1 est :
comme somme d'un entier et d'une fraction inférieure à 1 est : 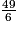 = 8 +
= 8 + 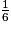 .
.
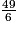 comme somme d'un entier et d'une fraction inférieure à 1 est :
comme somme d'un entier et d'une fraction inférieure à 1 est : 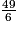 = 8 +
= 8 + 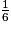 .
.Encadrez la fraction 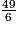 par deux entiers consécutifs.
par deux entiers consécutifs.
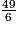 par deux entiers consécutifs.
par deux entiers consécutifs. Écrivez les réponses dans les zones colorées.
On a : < 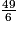 <
<
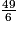 <
< Si l'écriture de la fraction 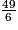 comme somme d'un entier et d'une fraction inférieure à 1 est
comme somme d'un entier et d'une fraction inférieure à 1 est 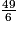 = 8 +
= 8 + 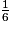 , on a :
, on a :
8 <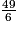 < 9.
< 9.
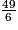 comme somme d'un entier et d'une fraction inférieure à 1 est
comme somme d'un entier et d'une fraction inférieure à 1 est 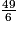 = 8 +
= 8 + 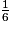 , on a :
, on a :8 <
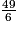 < 9.
< 9.Exercice n°4
Encadre la fraction 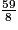 avec deux entiers consécutifs.
avec deux entiers consécutifs.
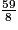 avec deux entiers consécutifs.
avec deux entiers consécutifs. Écrivez les réponses dans les zones colorées.
On a : < 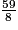 <
<
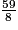 <
< 7×8 = 56 < 59 < 8 × 8 = 64 donc 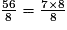 <
< 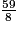 <
< 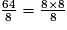 .
.
L'encadrement de la fraction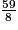 par deux entiers consécutifs est donc : 7 <
par deux entiers consécutifs est donc : 7 < 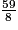 < 8.
< 8.
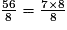 <
< 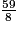 <
< 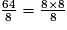 .
.L'encadrement de la fraction
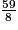 par deux entiers consécutifs est donc : 7 <
par deux entiers consécutifs est donc : 7 < 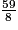 < 8.
< 8.
