Une division décimale « tombe juste » lorsque le reste est nul.
Exemple 1 :
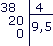 |
• En 38, combien de fois 4 ? 9 fois et il reste 2.
Pour continuer la division, on met une virgule au quotient après le 9 et on pose le chiffre 0 à droite de 2.
Pour continuer la division, on met une virgule au quotient après le 9 et on pose le chiffre 0 à droite de 2.
• En 20, combien de fois 4 ? 5 fois.
• La division « tombe juste » : 9,5 est l'écriture décimale exacte du quotient 38 ÷ 4.
On écrit : 38 = 4 × 9,5.
On écrit : 38 = 4 × 9,5.
Exemple 2 : 1,92 ÷ 0,3 = ?
• Pour ne plus avoir de virgule au diviseur, on multiplie par 10 le dividende et le diviseur.
• On divise donc 19,2 par 3.
En 19, combien de fois 3 ? 6 fois et il reste 1,…
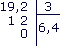 |
• 6,4 est l'écriture décimale exacte du quotient 1,92 ÷ 0,3.
Exercice n°1
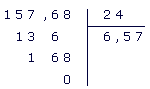 |
Complète le détail de cette opération par des nombres.
Écrivez les réponses dans les zones colorées.
Le nombre 15 étant inférieur à 24, on commence la division avec les premiers chiffres du dividende.
En 157, combien de fois 24 ? fois.
On calcule fois 24, on obtient 144.
On soustrait 144 à . Il reste unités.
On abaisse le 6, on place une virgule au quotient.
En 136, combien de fois ? 5 fois.
On calcule 5 fois 24, on obtient .
On soustrait 120 à 136. Il reste 16 dixièmes.
On abaisse le .
En combien de fois 24 ? 7 fois.
On calcule fois 24, on obtient 168.
est le quotient dans la division de 157,68 par 24.
En 157, combien de fois 24 ? fois.
On calcule fois 24, on obtient 144.
On soustrait 144 à . Il reste unités.
On abaisse le 6, on place une virgule au quotient.
En 136, combien de fois ? 5 fois.
On calcule 5 fois 24, on obtient .
On soustrait 120 à 136. Il reste 16 dixièmes.
On abaisse le .
En combien de fois 24 ? 7 fois.
On calcule fois 24, on obtient 168.
est le quotient dans la division de 157,68 par 24.
Ici la division tombe juste : 6,57 est le quotient exact de 157,68 par 24.
Exercice n°2
Fais les exercices dans l'ordre proposé.
a. Complète avec une virgule le résultat des opérations, de façon que les égalités soient vraies.
Tu peux utiliser des ordres de grandeur.
Tu peux utiliser des ordres de grandeur.
Écrivez les réponses dans les zones colorées.
8,04 ÷ 6 = 134
122,4 ÷ 6 = 204
223,4 ÷ 71 = 315
b. On sait que 124 × 235 = 29 140.
Sans effectuer les opérations, donne le résultat des divisions suivantes.
Sans effectuer les opérations, donne le résultat des divisions suivantes.
Écrivez les réponses dans les zones colorées.
2 914 ÷ 235 =
2 914 ÷ 23,5 =
2 914 ÷ 1,24 =
29,14 ÷ 1,24 =
a. L'ordre de grandeur de 8,04 est 8, l'ordre de grandeur du quotient de 8 par 6 est 1.
b. De la première égalité, on peut déduire que :
29 140 ÷ 235 = 124
29 140 ÷ 124 = 235
Observons la première division à compléter. 2 914, c'est 29 140 divisé par 10, donc le quotient de 2 914 par 235 est égal à 124 divisé par 10.
29 140 ÷ 235 = 124
29 140 ÷ 124 = 235
Observons la première division à compléter. 2 914, c'est 29 140 divisé par 10, donc le quotient de 2 914 par 235 est égal à 124 divisé par 10.

