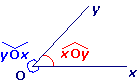
• Deux demi-droites [Ox) et [Oy) définissent deux angles :
[Ox) et [Oy) sont ses côtés.
- l'un, noté
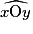, est appelé angle saillant ; - l'autre, noté
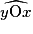, est appelé angle rentrant.
[Ox) et [Oy) sont ses côtés.
 |
• Deux angles sont adjacents :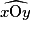 
et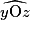 
sont adjacents.
- s'ils ont le même sommet ;
- s'ils ont un côté commun ;
- s'ils sont situés de part et d'autre du côté commun.
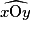et 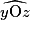sont adjacents. |
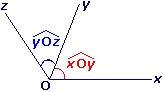Exercice n°1
Comment noter l'angle dessiné ci-dessous ?
 |
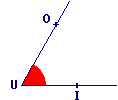1. 
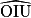
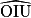
Cochez la bonne réponse.
| ||
|
2. 
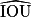
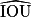
Cochez la bonne réponse.
| ||
|
3. 
Cochez la bonne réponse.
| ||
|
4. 
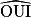
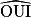
Cochez la bonne réponse.
| ||
|
• Dans le nom d'un angle, tel que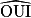 
, la lettre du milieu désigne le sommet de l'angle.
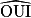, la lettre du milieu désigne le sommet de l'angle.• Ici, l'angle peut aussi être noté 
.
.Exercice n°2
Pourquoi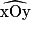 
et 
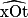ne sont-ils pas adjacents ?
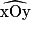et 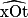ne sont-ils pas adjacents ? |
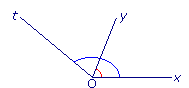1. Ils n'ont pas le même sommet.
Cochez la bonne réponse.
| ||
|
2. Ils ne sont pas situés de part et d'autre du côté commun.
Cochez la bonne réponse.
| ||
|
3. Ils n'ont pas de côté commun.
Cochez la bonne réponse.
| ||
|
• Les angles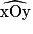 
et 
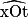ont le même sommet et un côté commun [Ox).
Mais ils sont tous les deux du même côté de [Ox).
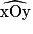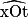et ont le même sommet et un côté commun [Ox). Mais ils sont tous les deux du même côté de [Ox).
• Les angles adjacents de la figure son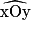t 
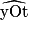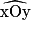et 
.
et 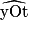.Exercice n°3
 |
Observe la figure puis coche la réponse exacte.
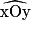et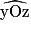 
sont :
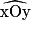et 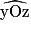sont : Cochez la bonne réponse.
| ||
| ||
|
Deux angles sont adjacents quand ils ont le même sommet, un côté commun et qu'ils sont situés de part et d'autre de ce côté commun.
Exercice n°4
Complète les phrases suivantes.
Écrivez les réponses dans les zones colorées.
1. Un angle a pour mesure 90°.
2. Un angle saillant a une mesure inférieure à °.
3. Un angle a une mesure supérieure à 180°.
4. Deux angles sont adjacents s'ils ont un sommet , un commun et s'ils sont situés de part et d'autre de ce .
