Dans un problème d'aires, il faut se souvenir que les unités d'aires vont de 100 en 100.
Avant de faire les calculs, il faut toujours convertir toutes les grandeurs dans la même unité.
Attention en particulier aux problèmes utilisant des unités agraires (l'are et l'hectare).
• Rappel :
1 a = 1 dam2 = 100 m2
1 ha = 1 hm2 = 100 dam2 = 10 000 m2
1 a = 1 dam2 = 100 m2
1 ha = 1 hm2 = 100 dam2 = 10 000 m2
• Exemple de problème :
Sur un terrain d'1 ha, on utilise 400 m2 pour construire une maison.
Quelle est l'aire restante en m2 ?
Aire restante en m2 : 10 000 – 400 = 9 600.
Sur un terrain d'1 ha, on utilise 400 m2 pour construire une maison.
Quelle est l'aire restante en m2 ?
Aire restante en m2 : 10 000 – 400 = 9 600.
Exercice n°1
Une voiture occupe en moyenne 15 m2 au sol.
Combien de voitures pourra-t-on garer dans un champ de 0,45 ha ?
Écrivez les réponses dans les zones colorées.
1. On convertit : ha = m2.
2. On calcule : ÷ 15 = .
3. Conclusion : on pourra garer voitures dans ce champ.
• Pour résoudre ce problème, il faut :
- convertir 0,45 ha en m2 : 1 ha = 10 000 m2, alors 0,45 ha = … m2 ;
- puis effectuer une division.
• Tu dois trouver un nombre entier de voitures.
Attention à la conversion : 1 ha = 10 000 m2 ; donc 0,45 ha = 4 500 m2.
Exercice n°2
1. Pour carreler une cuisine, on utilise 8 200 carreaux de 25 cm2.
Quelle est, en m2, l'aire de la cuisine ?
Quelle est, en m2, l'aire de la cuisine ?
Écrivez les réponses dans les zones colorées.
Aire en cm2 = 25 × = .
Aire en m2 = .
Aire en m2 = .
2. Un terrain de 2 ha est divisé en 5 parties égales.
Quelle est, en m2, l'aire de chaque partie ?
Quelle est, en m2, l'aire de chaque partie ?
Écrivez les réponses dans les zones colorées.
Aire de chaque partie en m2 :
÷ =
÷ =
Attention aux conversions.
• 205 000 cm2 = 2 050 dm2 = 20,5 m2
• Rappel : 1 ha = 10 000 m2.
Exercice n°3
Convertis les aires suivantes comme demandé.
Écrivez les réponses dans les zones colorées.
a. 23,6 km2 = hm2
b. 152 dam2 = hm2
c. 0,856 km2 = a
N'oublie pas que l'are (a) est une unité agraire valant 1 dam2.
Exercice n°4
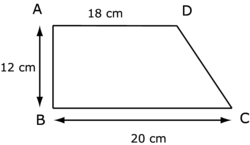
Quelle est l'aire du trapèze rectangle ABCD représenté ci-dessous ?
 |
Cochez la bonne réponse.
| ||
| ||
| ||
|
Partage le trapèze en deux parties : un rectangle et un triangle rectangle.
L'aire du trapèze est égale à la somme des aires du rectangle ABHD et du triangle rectangle DHC. On a : CH = BC − BH = 20 − 18 = 2.
Le calcul donne : 12 × 18 +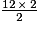
= 216 + 12 = 228 cm2.
Le calcul donne : 12 × 18 +
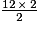= 216 + 12 = 228 cm2. |
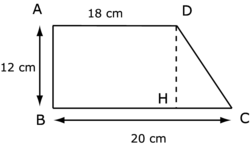