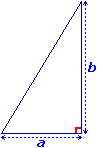
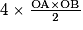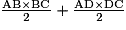• L'aire du triangle rectangle est donnée par la formule : A = 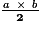
où a et b sont les mesures des côtés de l'angle droit.
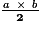
où a et b sont les mesures des côtés de l'angle droit.
 |
• Si a = 14 cm et b = 28 cm, alors on a : A = 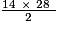 ; A = 196 cm2.
; A = 196 cm2.
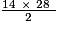 ; A = 196 cm2.
; A = 196 cm2.• Quand on connaît l'aire d'un triangle rectangle et la mesure d'un des côtés de l'angle droit (a ou b), on peut calculer la mesure de l'autre en s'aidant des formules :
a =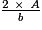 et b =
et b = 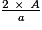 .
.
a =
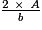 et b =
et b = 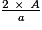 .
.Exemple : si l'aire d'un triangle rectangle est 1,35 dam2 et si un côté de l'angle droit mesure 15 m, alors l'autre côté mesure, en m, après conversion 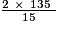 = 18.
= 18.
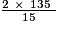 = 18.
= 18.Exercice n°1
Complète le tableau suivant.
Il s'agit de triangles rectangles dont les côtés de l'angle droit ont pour mesures a et b.
Écrivez les réponses dans les zones colorées.
| a (en m) | 10 | 3,5 | | 12 |
| b (en m) | 7 | 0,8 | 20 | |
| Aire en m2) | | | 500 | 27 |
Colonnes 1 et 2
Applique la formule du calcul de l'aire d'un triangle rectangle : aire = (a × b) ÷ 2.
Applique la formule du calcul de l'aire d'un triangle rectangle : aire = (a × b) ÷ 2.
Colonnes 3 et 4
Commence par calculer 2 × aire.
C'est le résultat de a × b.
Déduis-en a ou b à l'aide d'une division.
Commence par calculer 2 × aire.
C'est le résultat de a × b.
Déduis-en a ou b à l'aide d'une division.
• (10 × 7) ÷ 2
(3,5 × 0,8) ÷ 2
(3,5 × 0,8) ÷ 2
• 2 × 500 = 1 000 donc 1 000 = a × 20
et a = 1 000 ÷ 20.
et a = 1 000 ÷ 20.
Exercice n°2
Un terrain ayant la forme d'un triangle rectangle a la même aire qu'un terrain carré de 20 m de côté.
L'un des côtés de l'angle droit du terrain triangulaire mesure 100 m.
L'un des côtés de l'angle droit du terrain triangulaire mesure 100 m.
Combien mesure l'autre côté ? Complète.
Écrivez les réponses dans les zones colorées.
• Aire du terrain carré : m2.
• Mesure du côté : m.
• Pense que :
- l'aire d'un carré est égale à : côté × côté ;
- l'aire d'un triangle rectangle est égale à : (a × b) ÷ 2.
• Calcule : 2 × aire du carré.
Tu peux alors écrire :
2 × aire du carré = a × b
2 × aire du carré = 100 × b
Déduis-en b à l'aide d'une division.
Tu peux alors écrire :
2 × aire du carré = a × b
2 × aire du carré = 100 × b
Déduis-en b à l'aide d'une division.
Exercice n°3
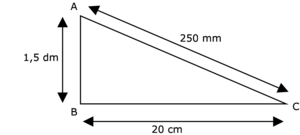
Quelle est l'aire du triangle rectangle ABC représenté ci-dessous ?
 |
Cochez la bonne réponse.
| ||
| ||
| ||
|
Les mesures des côtés de l'angle droit doivent être exprimées dans la même unité.
1,5 dm = 15 cm
L'aire du triangle rectangle ABC est égale à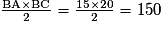 .
.
L'aire est égale à 150 cm2.
L'aire du triangle rectangle ABC est égale à
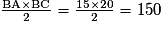 .
.L'aire est égale à 150 cm2.
Exercice n°4
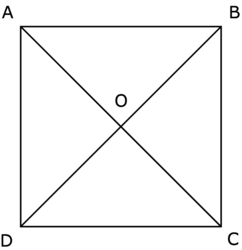
Quelle est l'aire du carré ci-dessous ?
 |
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
Le carré ABCD peut être divisé en deux ou quatre triangles rectangles.
• L'aire d'un carré est égale au produit du côté par lui-même.
• 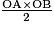 est l'aire du triangle rectangle AOB ; le carré est formé de quatre triangles rectangles identiques au triangle AOB.
est l'aire du triangle rectangle AOB ; le carré est formé de quatre triangles rectangles identiques au triangle AOB.
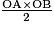 est l'aire du triangle rectangle AOB ; le carré est formé de quatre triangles rectangles identiques au triangle AOB.
est l'aire du triangle rectangle AOB ; le carré est formé de quatre triangles rectangles identiques au triangle AOB.• 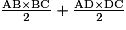 est la somme des aires des triangles rectangles ABC et ADC.
est la somme des aires des triangles rectangles ABC et ADC.
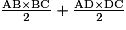 est la somme des aires des triangles rectangles ABC et ADC.
est la somme des aires des triangles rectangles ABC et ADC.