Énoncé
6 points
La distance parcourue par un véhicule entre le moment où le conducteur voit un obstacle et l'arrêt complet du véhicule est schématisée ci-dessous :
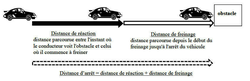 |
1. Un scooter roulant à 45 km/h freine en urgence pour éviter un obstacle. À cette vitesse, la distance de réaction est égale à 12,5 m et la distance de freinage à 10 m. Quelle est la distance d'arrêt ?
Utilisez la formule donnée dans l'énoncé.
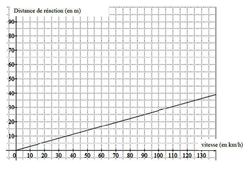
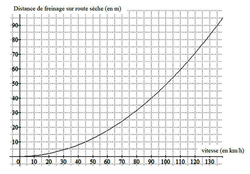
2. Les deux graphiques donnés en annexe représentent, dans des conditions normales et sur route sèche, la distance de réaction et la distance de freinage en fonction de la vitesse du véhicule. En utilisant ces graphiques, répondre aux questions suivantes.
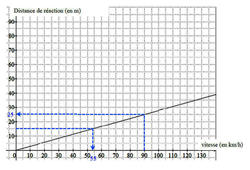
a) La distance de réaction est de 15 m. À quelle vitesse roule-t-on ? (Aucune justification n'est attendue)
Vous devez trouver l'antécédent de 15 par la fonction représentée dans le premier graphique.
b) La distance de freinage du conducteur est-elle proportionnelle à la vitesse de son véhicule ?
Que pouvez-vous dire à propos de la représentation graphique d'une situation de proportionnalité ? Est-ce le cas pour la représentation graphique de la distance de freinage en fonction de la vitesse du véhicule ?
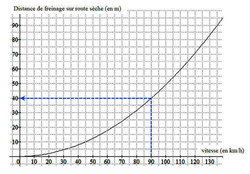
c) Déterminer la distance d'arrêt pour une voiture roulant à 90 km/h.
Il s'agit d'additionner la distance de réaction et la distance de freinage pour une voiture roulant à 90 km/h. Vous devez trouver ces deux valeurs par une lecture graphique sur chacun des deux graphiques.
3. La distance de freinage en mètres, d'un véhicule sur route mouillée, peut se calculer à l'aide de la formule suivante, où v est la vitesse en km/h du véhicule :
distance de freinage sur route mouillée =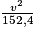 .
.
Calculer au mètre près la distance de freinage sur route mouillée à 110 km/h.
distance de freinage sur route mouillée =
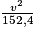 .
.Calculer au mètre près la distance de freinage sur route mouillée à 110 km/h.
Vous devez trouver une distance comprise entre 70 et 80 mètres en utilisant la formule donnée.
Annexe
 |
 |
Corrigé
1.
D'après l'énoncé, la distance d'arrêt est la somme de la distance de réaction et de la distance de freinage.
Pour un scooter roulant à 45 km/h qui freine en urgence pour éviter un obstacle, la distance d'arrêt est donc de 12,5 + 10 = 22,5 m.
Pour un scooter roulant à 45 km/h qui freine en urgence pour éviter un obstacle, la distance d'arrêt est donc de 12,5 + 10 = 22,5 m.
2.
a) Il s'agit de trouver l'antécédent de 15 par la fonction représentant la distance de réaction en fonction de la vitesse.
Graphiquement, lorsque la distance de réaction est de 15 m, la vitesse est d'environ 55 km/h.
Graphiquement, lorsque la distance de réaction est de 15 m, la vitesse est d'environ 55 km/h.
 |
b) Une situation de proportionnalité est représentée graphiquement par une droite passant par l'origine du repère.
Le graphique représentant la distance de freinage en fonction de la vitesse n'est pas une droite, donc la distance de freinage n'est pas proportionnelle à la vitesse de son véhicule.
Le graphique représentant la distance de freinage en fonction de la vitesse n'est pas une droite, donc la distance de freinage n'est pas proportionnelle à la vitesse de son véhicule.
c) D'après l'énoncé, la distance d'arrêt est la somme de la distance de réaction et de la distance de freinage.
Il s'agit de déterminer graphiquement l'image de 90 par chacune des deux représentations graphiques.
Pour une voiture roulant à 90 km/h, la distance de réaction est de 25 m. (Voir graphique ci-dessus)
Pour une voiture roulant à 90 km/h, la distance de freinage est de 40 m. (Voir graphique ci-après)
Il s'agit de déterminer graphiquement l'image de 90 par chacune des deux représentations graphiques.
Pour une voiture roulant à 90 km/h, la distance de réaction est de 25 m. (Voir graphique ci-dessus)
Pour une voiture roulant à 90 km/h, la distance de freinage est de 40 m. (Voir graphique ci-après)
Pour une voiture roulant à 90 km/h, la distance d'arrêt est de 25 + 40 = 65 m.
 |
3. À 110 km/h, la distance de freinage sur route mouillée est :
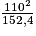 =
= 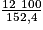
 79 m au mètre près.
79 m au mètre près.
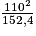 =
= 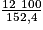
 79 m au mètre près.
79 m au mètre près. 
