Calcul de la moyenne d'un élève
Voici les notes d'un élève :
| Discipline | Note | Coefficient |
| Français | 11/20 | 4 |
| Maths | 06/20 | 3 |
| Anglais | 06/20 | 2 |
| E.P.S. | 10/20 | 1 |
Pour calculer sa moyenne pondérée M :
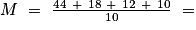 8,4.
8,4.
- on fait le produit de chaque note par son coefficient ;
- puis la somme de ces produits ;
- et on divise cette somme par la somme des coefficients :
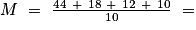 8,4.
8,4.Autre calcul de moyenne
Voici les notes obtenues par une classe de 25 élèves en mathématiques.
Les notes sont regroupées en « intervalles » ou « classes ».
Les notes sont regroupées en « intervalles » ou « classes ».
| Notes | [2 ; 8[ | [8 ; 14[ | [14 ; 20[ |
| Effectif | 12 | 8 | 5 |
Pour calculer la moyenne générale, on prend la note moyenne de chaque classe (le centre) et on l'affecte du nombre d'élèves correspondant : 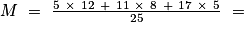 9,32.
9,32.
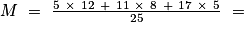 9,32.
9,32.Exercice n°1
Voici les notes obtenues en français par Olivier, pour le 1er trimestre.
| | Notes | Coefficient |
| Lecture de textes | 4 et 12 | 2 |
| Expression écrite | 7 et 13 | 3 |
| Maîtrise de la langue | 5 et 11 | 1 |
Calcule la moyenne obtenue par Olivier.
Écrivez la réponse dans la zone colorée.
Réponse : .
Il faut tenir compte des coefficients.
La moyenne M est alors :
M =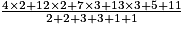 ,
,
soit M =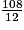 = 9.
= 9.
M =
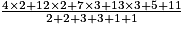 ,
,soit M =
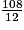 = 9.
= 9.Exercice n°2
Dans une classe, on relève la somme en euros dont dispose chaque élève par mois et on regroupe les résultats dans un tableau.
| Somme en € | ]0 ; 10] | ]10 ; 20] | ]20 ; 30] |
| Effectif | 12 | 10 | 3 |
Calcule la somme moyenne d'argent de poche des élèves de cette classe.
Écrivez la réponse dans la zone colorée.
Réponse : €.
Le centre de l'intervalle ]0 ; 10] est 5.
Le centre de l'intervalle ]10 ; 20] est 15.
Le centre de l'intervalle ]20 ; 30] est 25.
Le centre de l'intervalle ]10 ; 20] est 15.
Le centre de l'intervalle ]20 ; 30] est 25.
La moyenne est alors :
M =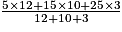 ,
,
soit M =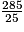 = 11,40.
= 11,40.
M =
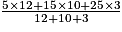 ,
,soit M =
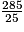 = 11,40.
= 11,40.Exercice n°3
Lors d'un examen comportant cinq épreuves, un candidat a obtenu les notes suivantes aux quatre premières épreuves :
| Matière | Français | Maths | Sciences | Hist.-géo. | Anglais |
| Note sur 20 | 7 | 15 | 8 | 11 | |
| Coefficient | 3 | 5 | 3 | 2 | 2 |
Calcule quelle note minimum il doit obtenir en anglais pour que sa moyenne générale soit égale à 10.
Écrivez la réponse dans la zone colorée.
Il doit obtenir la note minimum de .
On cherche x tel que 10 = 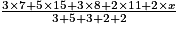 , c'est-à-dire 10 =
, c'est-à-dire 10 = 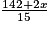 . Donc 142 + 2x = 150, d'où x = 4.
. Donc 142 + 2x = 150, d'où x = 4.
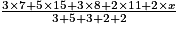 , c'est-à-dire 10 =
, c'est-à-dire 10 = 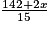 . Donc 142 + 2x = 150, d'où x = 4.
. Donc 142 + 2x = 150, d'où x = 4.Exercice n°4
Voici les informations fournies cette semaine par le service comptable d'une banque :
| Somme déposée en € | 100 | 300 | 500 | 1000 | 5000 |
| Effectif | 22 | 28 | 25 | 18 | 7 |
Réponds aux questions.
Écrivez les réponses dans les zones colorées.
a. Combien de clients ont déposé de l'argent cette semaine-là ?
Nombre de clients :
Nombre de clients :
b. Quelle est la moyenne m des montants des sommes déposées ?
m = €
m = €
a. Pour trouver le nombre de clients, on ajoute les effectifs qui figurent sur la seconde ligne du tableau.
b. La moyenne m est égale à 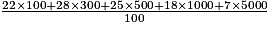 .
.
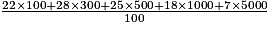 .
.Exercice n°5
Le tableau suivant donne la répartition des véhicules de l'entreprise Infomed selon la distance parcourue en une semaine.
| Distance d en km | Effectif |
d  100 100 | 18 |
100 < d  200 200 | 55 |
200 < d  300 300 | 112 |
300 < d  400 400 | 36 |
400 < d  500 500 | 11 |
En remplaçant chaque classe par son centre, calcule la distance moyenne parcourue par ces véhicules en une semaine.
Écrivez la réponse dans la zone colorée.
Distance moyenne = km à 1 km près par excès.
Pour chaque classe, on calcule le produit de l'effectif par le centre de la classe :
50 × 18 = 900 ; 150 × 55 = 8 250 ; 250 × 112 = 28 000 ; 350 × 36 = 12 600 et 450 × 11 = 4 950.
50 × 18 = 900 ; 150 × 55 = 8 250 ; 250 × 112 = 28 000 ; 350 × 36 = 12 600 et 450 × 11 = 4 950.
On ajoute ces produits, on trouve 54 700 qu'on divise par l'effectif total 232.
On obtient 235,77 ; soit 236 km à 1 km près par excès.
On obtient 235,77 ; soit 236 km à 1 km près par excès.

