Définition
La médiane d'une série statistique est la valeur du caractère qui partage la population en deux effectifs égaux. Il ne faut pas la confondre avec la moyenne.
Exemple :
18 élèves parcourent une distance de 1 à 4 km pour aller à l'école : 6 élèves parcourent 1 km, 6 parcourent 2 km, 3 parcourent 3 km et 3 parcourent 4 km.
Exemple :
18 élèves parcourent une distance de 1 à 4 km pour aller à l'école : 6 élèves parcourent 1 km, 6 parcourent 2 km, 3 parcourent 3 km et 3 parcourent 4 km.
| Distance (km) | 1 | 2 | 3 | 4 |
| Effectif | 6 | 6 | 3 | 3 |
| Effectif cumulé | 6 | 12 | 15 | 18 |
Nous allons chercher la médiane de cet effectif de 18 élèves. Pour cela, il existe deux méthodes : numérique et graphique.
Résolution numérique
Méthode :
- 1. Calculer l'effectif total N (ici 18) ;
- 2. Ordonner les valeurs de la série dans l'ordre croissant ;
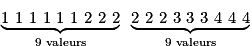
La valeur 2 km en est la médiane : elle partage l'effectif total des salariés en deux groupes égaux.
- 3. Déterminer la médiane :
- Si N est impair (ce qui n'est pas le cas ici), la médiane est la valeur située à la position (N + 1) / 2.
- Si N est pair (c'est le cas ici avec N = 18), la médiane est la moyenne des deux valeurs situées entre la N / 2ème position et la (N / 2 + 1)ème position. Ici entre la 9ème et la 10ème position, c'est-à-dire 2 km.
Résolution graphique
La médiane peut aussi être déterminée, au moyen du diagramme des effectifs cumulés. on cherche la valeur correspondant à la moitié de l'effectif total (ici : 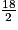 = 9).
= 9).
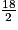 = 9).
= 9).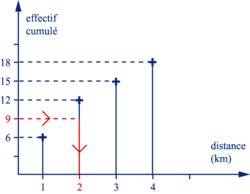 |
Exercice n°1
Vrai ou faux ?
1. La médiane d'une série de 75 notes rangées par ordre croissant est la 38e note.
Cochez la bonne réponse.
| ||
|
2. La médiane d'une série de notes n'est pas toujours l'une des notes de la série.
Cochez la bonne réponse.
| ||
|
3.
La note médiane est 6.
| Note | 3 | 4,5 | 6 | 7,8 | 9 |
| Effectif | 2 | 3 | 1 | 2 | 1 |
La note médiane est 6.
Cochez la bonne réponse.
| ||
|
3. La série statistique est :
3 ; 3 ; 4,5 ; 4,5 ; 4,5 ; 6 ; 7,8 ; 7,8 ; 9.
La note qui sépare cette série en deux parties de même effectif est 4,5.
3 ; 3 ; 4,5 ; 4,5 ; 4,5 ; 6 ; 7,8 ; 7,8 ; 9.
La note qui sépare cette série en deux parties de même effectif est 4,5.
Exercice n°2
Coche la bonne réponse.
La médiane d'une série statistique n'est jamais égale à la moyenne.
Cochez la bonne réponse.
| ||
|
La médiane d'une série statistique de 43 notes rangées dans l'ordre croissant est la 22e note.
Cochez la bonne réponse.
| ||
|
La médiane d'une série statistique est toujours une valeur du caractère étudié.
Cochez la bonne réponse.
| ||
|
Exercice n°3
Soit un groupe de 19 élèves.
Les notes obtenues lors d'un test sont regroupées dans un tableau :
Les notes obtenues lors d'un test sont regroupées dans un tableau :
| Note | 6 | 7 | 8 | 9 | 11 | 12 | 13 | 15 |
| Effectif | 3 | 3 | 2 | 3 | 2 | 3 | 2 | 1 |
Calcule la médiane de cette série de notes.
Écrivez la réponse dans la zone colorée.
Réponse :
Il y a 19 notes : 19 = 2 × 9 + 1.
La médiane est la valeur qui partage les notes en deux groupes de 9.
3 + 3 + 2 = 8
8 + 3 = 11
La médiane est donc la note 9.
La médiane est la valeur qui partage les notes en deux groupes de 9.
| Note | 6 | 7 | 8 | 9 |
| Effectif | 3 | 3 | 2 | 3 |
3 + 3 + 2 = 8
8 + 3 = 11
La médiane est donc la note 9.
Exercice n°4
Voici le diagramme des effectifs cumulés correspondant à une série de notes.
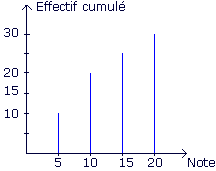 |
Détermine la médiane.
Écrivez la réponse dans la zone colorée.
La valeur de la médiane est : .
L'effectif total est 30.
La médiane est donc la valeur qui partage les notes en deux groupes de 15.
La médiane est donc la valeur qui partage les notes en deux groupes de 15.
En traçant une ligne horizontale à partir de l'effectif 15, on rencontre le bâton correspondant à la note 10.

