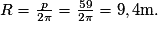Au cours des siècles, la Terre fut considérée tour à tour comme plate, sphérique, puis de nouveau plate et de nouveau sphérique… Les premières thèses sur la sphéricité de la Terre datent de l'Antiquité. La mesure du méridien terrestre a démontré que la Terre était bien sphérique. À présent, les images données par les satellites ne laissent aucun doute.
I. Que pensait-on dans l'Antiquité ?
• Le premier savant ayant étudié la forme de la Terre est Thalès (−625 ; −547). Il pense que la Terre est plate et qu'elle a la forme d'un disque flottant sur un océan infini.
• Plusieurs savants, comme Platon ou Eudoxe, affirment que la Terre est sphérique, mais ne savent pas le démontrer.
• Une véritable avancée a lieu avec Aristote (−384 ; −322), qui apporte des preuves scientifiques concernant la forme de la Terre et sa position dans l'Univers. Il constate qu'à chaque fois qu'il y a des éclipses de Lune, la forme réfléchie de l'ombre est courbée. Il observe également des changements dans l'aspect du ciel : des étoiles apparaissent au-dessus de l'horizon et d'autres disparaissent sous l'horizon dans la direction opposée. Il affirme néanmoins que la Terre est au centre de l'Univers, ce qui est faux.
• L'astronome Eratosthène (−273 ; −192) est le véritable fondateur de la géodésie, science qui consiste à mesurer et à représenter la surface terrestre. Il détermine le périmètre de la Terre et prouve définitivement la sphéricité de la Terre. En effet, Eratosthène apprend qu'à Syène (aujourd'hui Assouan) les rayons tombent à la verticale, atteignant le fond des puits à midi, le jour du solstice d'été. Or, à Alexandrie, ville située plus au nord, cela ne se produit pas. Il plante alors à Alexandrie un bâton vertical et mesure l'angle α entre le bâton et les rayons du soleil ; il trouve 1/50e de cercle, ce qui équivaut environ à : 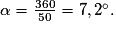
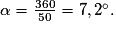
• Il interprète cette observation de la façon suivante : Il suppose que le Soleil est très éloigné de la Terre ; dans ces conditions, les rayons parvenant en n'importe quel point de la surface terrestre sont parallèles. Il attribue la différence des ombres à un effet de la rotondité de la Terre.
• Eratosthène sait également que les caravanes de chameaux partant de Syène mettent 50 jours pour arriver à Alexandrie en parcourant 100 stades par jour (le stade équivaut à 160 m). La distance est donc environ égale à d = 100 × 160 × 50 = 80 000 = 800 km. Ces éléments sont suffisants pour calculer le rayon de la Terre. En effet, d'après le théorème des angles alternes - internes, on trouve l'angle α au centre de la Terre.
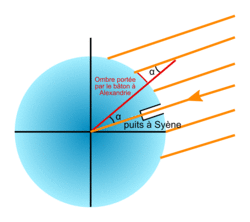 |
• Puisque la mesure de cet angle par Erathostène à Alexandrie donne 1/50e de cercle, la distance entre Syène et Alexandrie vaut 1/50e de la circonférence de la Terre. Or la distance entre les deux villes valant 800 km, cela donne une estimation de la circonférence de la Terre (en la supposant parfaitement sphérique) : d = 800 × 50 = 40 000 km, ce qui est très proche de la vraie valeur de 40 075 km.
• Deux siècles avant Eratosthène, Anaxagore disposait des mêmes observations que lui :
- La distance entre Alexandrie et Syène est égale à 5 000 stades, soit 800 km environ.
- Un gnomon (bâton) vertical planté à Syène n'a pas d'ombre à midi le jour du solstice d'été, alors que le même jour et à la même heure, les rayons du Soleil font un angle de 7° avec un gnomon vertical à Alexandrie.
• Anaxagore postule alors que la Terre est plate et que le Soleil n'en est pas suffisamment éloigné pour que ses rayons soient parallèles quand ils atteignent notre planète. En reprenant les mêmes observations, Eratosthène parvient à une conclusion différente.
Exercice n°1
Exercice n°1
II. Comment a-t-on déterminé la mesure du mètre ?
• Pendant la période agitée de la Révolution française, on a modifié la monnaie, le calendrier, la semaine de sept jours et même l'heure de 60 minutes. Il était question en outre de définir une nouvelle unité unique afin d'harmoniser les systèmes de mesure et d'ouvrir le marché. À l'époque, il existait environ 250 000 unités de poids et de longueur : le pied, le point, le pouce, la ligne… Certaines différaient même d'une province à l'autre.
• Deux scientifiques de renom, Pierre Méchain et Jean-Baptiste Delambre, astronomes et mathématiciens, sont chargés par le gouvernement révolutionnaire français de trouver un système de mesure universel, valable partout et non dépendant de l'Homme (pouce, pied…). Le mètre est alors choisi : le dix-millionième de la méridienne terrestre.
• Ces scientifiques décident de mesurer avec précision la longueur d'une portion de méridien de Dunkerque à Barcelone. La méthode consiste à mesurer une base de 11 km environ entre Melun et Lieusaint. La base est l'origine d'une opération de triangulation. Ainsi, de la mesure des angles, ils déduisent la distance Lieusaint-Malvoisine et celle-ci constitue la base d'un nouveau triangle dont le sommet sera Montlhéry. Des triangles formeront ainsi une chaîne ininterrompue le long de la méridienne.
•
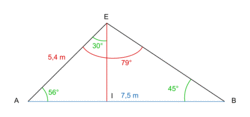
Simulons leur méthode :
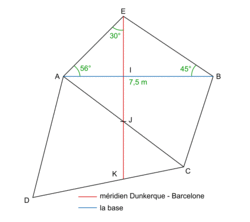 |
•
D'après la figure, dans le triangle ABE, on connaît un côté et deux angles. L'angle 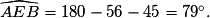 Avec la relation des sinus dans un triangle quelconque :
Avec la relation des sinus dans un triangle quelconque :
 Avec la relation des sinus dans un triangle quelconque :
Avec la relation des sinus dans un triangle quelconque : |
On peut donc écrire : 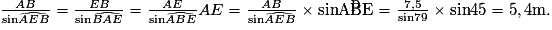
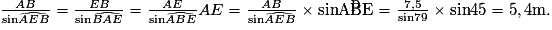
• Dans le triangle AEI, on connaît un côté et deux angles.
 |
L'angle 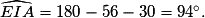 On peut donc écrire :
On peut donc écrire : 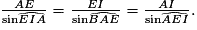
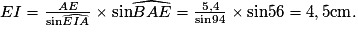
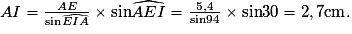
On mesure ensuite les angles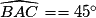 et
et 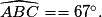
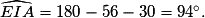 On peut donc écrire :
On peut donc écrire : 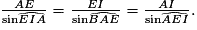
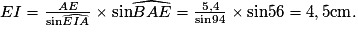
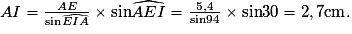
On mesure ensuite les angles
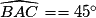 et
et 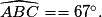
• Dans le triangle ABC, on connaît un côté et deux angles.
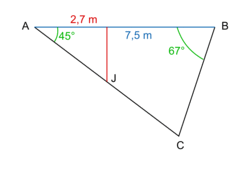 |
L'angle 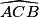 = 180 − 45 − 67 = 68°.
= 180 − 45 − 67 = 68°.
On peut donc écrire :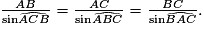
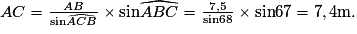
L'angle = 180 −
= 180 − 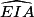 = 180 − 94 = 86°.
= 180 − 94 = 86°.
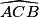 = 180 − 45 − 67 = 68°.
= 180 − 45 − 67 = 68°.On peut donc écrire :
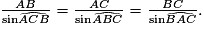
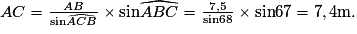
L'angle
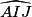 = 180 −
= 180 − 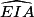 = 180 − 94 = 86°.
= 180 − 94 = 86°.• Dans le triangle AIJ, on connaît un côté et deux angles.
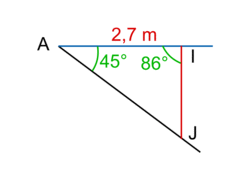 |
L'angle 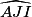 = 180 − 45 − 86 = 49°.
= 180 − 45 − 86 = 49°.
On peut donc écrire :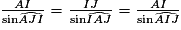
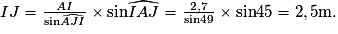
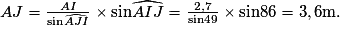
On mesure les angles = 64° et
= 64° et 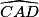 = 54°. L'angle
= 54°. L'angle 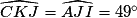 . La longueur JC = AC − AJ = 7,4 − 3,6 = 3,8 m.
. La longueur JC = AC − AJ = 7,4 − 3,6 = 3,8 m.
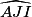 = 180 − 45 − 86 = 49°.
= 180 − 45 − 86 = 49°.On peut donc écrire :
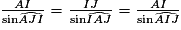
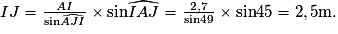
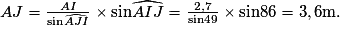
On mesure les angles
 = 64° et
= 64° et  = 54°. L'angle
= 54°. L'angle 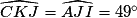 . La longueur JC = AC − AJ = 7,4 − 3,6 = 3,8 m.
. La longueur JC = AC − AJ = 7,4 − 3,6 = 3,8 m.• Dans le triangle CJK, on connaît un côté et deux angles.
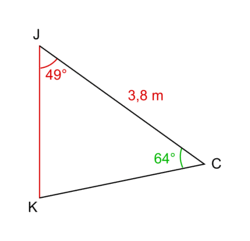 |
L'angle 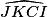 = 180 − 49 − 64 = 67°.
= 180 − 49 − 64 = 67°.
On peut donc écrire :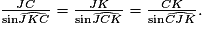
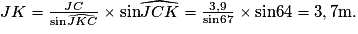
Finalement, la longueur EK vaut : EK = 4,5 + 2,5 + 3,7 = 10,7 m.
 = 180 − 49 − 64 = 67°.
= 180 − 49 − 64 = 67°.On peut donc écrire :
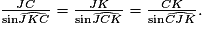
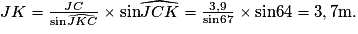
Finalement, la longueur EK vaut : EK = 4,5 + 2,5 + 3,7 = 10,7 m.
• La triangulation entre Dunkerque et Barcelone comporte 90 triangles ; 500 000 mesures d'angle ont été effectuées ; l'estimation faite en 1980 (mesures effectuées par satellite) de la distance Dunkerque-Barcelone diffère de la valeur de Delambre et Méchain de 10 mètres.
III. Comment calculer le rayon de la Terre à partir d'un méridien ?
• Un méridien est une ligne imaginaire qui joint le pôle Nord au pôle Sud de longueur environ 20 000 km. Sachant que le périmètre d'un cercle est donné par :
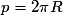
et que :
p = 2 × 20 000 = 40 000 km
on en déduit que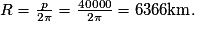
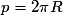
et que :
p = 2 × 20 000 = 40 000 km
on en déduit que
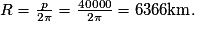
• Le rayon de la Terre est en moyenne égal à 6 371 km, qui est une valeur en accord avec celle calculée précédemment.
Exercice n°2Exercice n°3
Exercice n°2Exercice n°3
À retenir
Les scientifiques depuis l'Antiquité ont cru que la Terre était plate ou sphérique selon les courants de pensée. Eratosthène fut le premier à déterminer le diamètre de la Terre. Anaxagore avait tous les moyens de déterminer le diamètre de la Terre, mais étant donné qu'il a considéré que la Terre était plate, ses calculs étaient faux.La mesure d'un méridien a permis de définir la longueur du mètre. Celui-ci a pu être déterminé en mesurant la longueur de Dunkerque à Barcelone grâce à la méthode de la triangulation.
Avec la longueur d'un méridien, on peut calculer la longueur du rayon de la Terre.
Exercice n°1
Eratosthène détermine la longueur du périmètre de la Terre à Syène lors du solstice d'été. Quelle proposition est juste ?
Cochez la bonne réponse.
| ||
| ||
|
À Syène, le jour du solstice d'été, à midi, les rayons solaires sont parallèles aux parois du puits. Donc les rayons solaires arrivent perpendiculairement au sol. Cette particularité n'existe que sur le tropique du Cancer.
Exercice n°2
Déterminer la longueur de BC de la figure suivante :
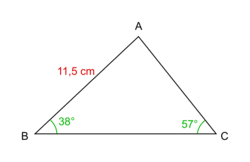 |
Donnée : 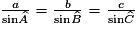
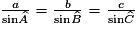
Cochez la bonne réponse.
| ||
| ||
|
Déterminons l'angle manquant :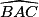 = 180 − 38 − 57 = 85°.
= 180 − 38 − 57 = 85°.
Dans le triangle ABC, on peut écrire :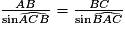 .
.
D'où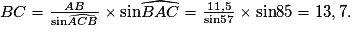
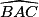 = 180 − 38 − 57 = 85°.
= 180 − 38 − 57 = 85°.Dans le triangle ABC, on peut écrire :
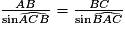 .
.D'où
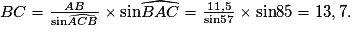
Exercice n°3
Si le périmètre d'un cercle est de 59 m, son rayon est :
Cochez la bonne réponse.
| ||
| ||
|
Le périmètre d'un cercle est donné par 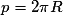 . On en déduit que
. On en déduit que 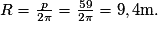
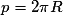 . On en déduit que
. On en déduit que