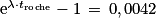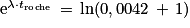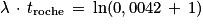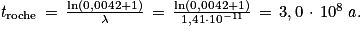Énoncé
Exercice sur 6 points
Les phénomènes de radioactivité permettent, en géologie, la datation des roches. Il est par exemple possible d'utiliser le strontium 87 (87Sr), qui est notamment issu de la désintégration du rubidium 87 (87Rb), lui-même également présent dans une roche.
Les objectifs de cet exercice sont d'étudier le principe de la datation au strontium 87, puis d'utiliser des résultats d'analyse pour déterminer l'âge d'une roche du site de Meymac situé dans le département de la Corrèze, site âgé de plusieurs centaines de millions d'années.
Les phénomènes de radioactivité permettent, en géologie, la datation des roches. Il est par exemple possible d'utiliser le strontium 87 (87Sr), qui est notamment issu de la désintégration du rubidium 87 (87Rb), lui-même également présent dans une roche.
Les objectifs de cet exercice sont d'étudier le principe de la datation au strontium 87, puis d'utiliser des résultats d'analyse pour déterminer l'âge d'une roche du site de Meymac situé dans le département de la Corrèze, site âgé de plusieurs centaines de millions d'années.
 |
Données :
- temps de demi-vie du noyau de rubidium 87 exprimé en années (a) : t1/2 = 49,2 × 109 a ;
- constante radioactive du noyau de rubidium 87 : λ = 1,41 × 10−11 a−1 ;
- on suppose qu'une datation d'un échantillon de 1 g de roche par le rubidium 87 radioactif est possible tant qu'il reste au moins Nmin = 2,0 × 109 noyaux de rubidium 87 dans l'échantillon ;
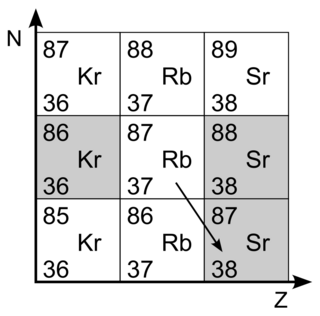
- extrait du diagramme (N,Z) : les cases grises indiquent les éléments stables.
 |
1. Le rubidium 87, un isotope radioactif adapté pour dater une roche
Q1. Rappeler la définition de noyaux isotopes.
Q2. Écrire l'équation de la désintégration du rubidium 87 indiquée par la flèche sur l'extrait du diagramme (N,Z).
Q3. Préciser à quel type de désintégration correspond cette transformation nucléaire.
On estime qu'un échantillon de 1 g de roche du site de Meymac contenait à sa formation NRb(0) = 5,8 × 1020 noyaux de rubidium 87. On souhaite déterminer l'âge maximal d'une roche qu'il serait possible de déterminer par une datation au rubidium 87 d'un échantillon de 1 g.
Q4. Rappeler la définition du temps de demi-vie t1/2.
Q5. Déterminer, en justifiant le résultat, le nombre maximal de demi-vies après lequel il reste suffisamment de rubidium 87 dans l'échantillon pour qu'on puisse le détecter.
On remarquera que le rapport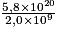 est compris entre 238 et 239.
est compris entre 238 et 239.
Q6. Justifier que le rubidium 87 est adapté pour dater un échantillon de 1 g de roche du site de Meymac.
Q2. Écrire l'équation de la désintégration du rubidium 87 indiquée par la flèche sur l'extrait du diagramme (N,Z).
Q3. Préciser à quel type de désintégration correspond cette transformation nucléaire.
On estime qu'un échantillon de 1 g de roche du site de Meymac contenait à sa formation NRb(0) = 5,8 × 1020 noyaux de rubidium 87. On souhaite déterminer l'âge maximal d'une roche qu'il serait possible de déterminer par une datation au rubidium 87 d'un échantillon de 1 g.
Q4. Rappeler la définition du temps de demi-vie t1/2.
Q5. Déterminer, en justifiant le résultat, le nombre maximal de demi-vies après lequel il reste suffisamment de rubidium 87 dans l'échantillon pour qu'on puisse le détecter.
On remarquera que le rapport
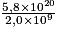 est compris entre 238 et 239.
est compris entre 238 et 239.Q6. Justifier que le rubidium 87 est adapté pour dater un échantillon de 1 g de roche du site de Meymac.
2. Décroissance radioactive du rubidium 87 dans une roche
La désintégration spontanée des noyaux de rubidium 87 présents dans un échantillon de 1 g de roche suit la loi de décroissance radioactive. Le nombre NRb(t) de noyaux de rubidium 87 présents dans un échantillon de roche à la date t est solution de l'équation différentielle suivante :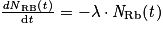
Q7. Vérifier que
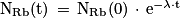 est solution de l'équation différentielle ci-dessus.
est solution de l'équation différentielle ci-dessus.On appelle tf la date à laquelle il reste Nmin = 2,0 × 109 noyaux de rubidium 87 dans l'échantillon.
Q8. Déterminer l'expression de tf en fonction de Nmin, NRb(0) et λ.
Q9. Calculer la valeur de tf puis la comparer à la réponse donnée dans la question Q6. Commenter.
3. Datation d'une roche du site de Meymac au strontium 87
On considère que la quantité de strontium 87 formé au cours du temps dans la roche est uniquement issue de la désintégration du rubidium 87. La quantité de strontium 87 présent dans la roche à une date t s'écrit :
NSr (t) = NSr (0) + NSr formé (t) Équation 1
avec :
Q11. En déduire l'égalité :
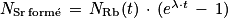 Équation 2
Équation 2
Les équations 1 et 2 permettent enfin d'obtenir l'équation 3 :
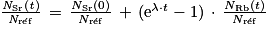 Équation 3
Équation 3
où Nréf représente le nombre de noyaux stables de strontium 86, supposé constant au cours du temps.
On écrit l'équation 3 sous la forme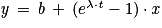 avec
avec 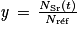 ,
, 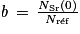 et
et 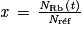 , dans laquelle :
, dans laquelle :
NSr (t) = NSr (0) + NSr formé (t) Équation 1
avec :
- NSr(t) : nombre de noyaux de strontium 87 présents à la date t ;
- NSr(0) : nombre de noyaux de strontium 87 présents à la date t = 0 ;
- NSr formé(t) : nombre de noyaux de strontium 87 formés par la désintégration du rubidium 87 à la date t.
Q11. En déduire l'égalité :
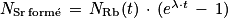 Équation 2
Équation 2Les équations 1 et 2 permettent enfin d'obtenir l'équation 3 :
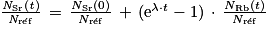 Équation 3
Équation 3où Nréf représente le nombre de noyaux stables de strontium 86, supposé constant au cours du temps.
On écrit l'équation 3 sous la forme
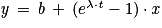 avec
avec 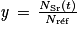 ,
, 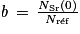 et
et 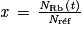 , dans laquelle :
, dans laquelle : - y et x sont des grandeurs mesurables par les géologues pour un ensemble d'échantillons prélevés dans une roche donnée ;
- b est une grandeur indépendante de l'échantillon.
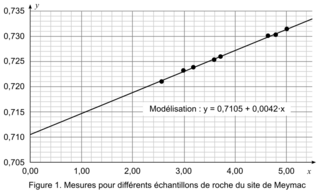 |
Q12. Déterminer l'âge troche de la roche du site de Meymac.
Corrigé
1. Le rubidium 87, un isotope radioactif adapté pour dater une roche
Q1.
C'est une question de cours : il faut se souvenir des particules qui constituent les noyaux (protons et neutrons).
Deux noyaux sont isotopes s'ils possèdent le même nombre de protons Z mais des nombres de neutrons N différents.
Q2.
L'équation de désintégration s'écrit en respectant la conservation du nombre de masse et la conservation du nombre de charges.
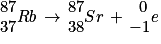
Q3.
C'est une question de cours : si la réaction produit un électron, il s'agit d'une désintégration 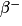 . Si la réaction produit un positon, il s'agit d'une désintégration
. Si la réaction produit un positon, il s'agit d'une désintégration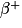 .
.
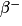 . Si la réaction produit un positon, il s'agit d'une désintégration
. Si la réaction produit un positon, il s'agit d'une désintégration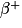 .
.Il s'agit d'une désintégration 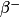 .
.
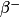 .
.Q4.
C'est une question de cours : il faut raisonner par rapport au nombre de noyaux initialement présents dans un échantillon.
Le temps de demi-vie correspond à la durée au bout de laquelle la moitié des noyaux radioactifs initialement présents dans l'échantillon se sont désintégrés.
Q5.
Il s'agit de déterminer le nombre de demi-vies tel que le nombre de noyaux restants soit supérieur à Nmin. Pour cela, il faut utiliser la définition de la demi-vie donnée à la question précédente et utiliser le rapport donné dans l'énoncé.
Après une durée t1/2, il reste un nombre de noyaux égal à 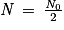 . Au bout d'une durée de n × t1/2 , il reste
. Au bout d'une durée de n × t1/2 , il reste 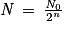 noyaux.
noyaux.
On cherche le nombre maximal de demi-vies n, tel que le nombre de noyaux restants N soit supérieur à Nmin.
On a donc :
N > Nmin soit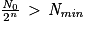
D'où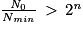 , c'est-à-dire
, c'est-à-dire 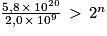
Or,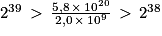
Donc n = 38.
Le nombre maximal de demi-vies est 38.
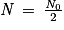 . Au bout d'une durée de n × t1/2 , il reste
. Au bout d'une durée de n × t1/2 , il reste 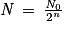 noyaux.
noyaux.On cherche le nombre maximal de demi-vies n, tel que le nombre de noyaux restants N soit supérieur à Nmin.
On a donc :
N > Nmin soit
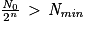
D'où
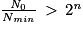 , c'est-à-dire
, c'est-à-dire 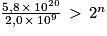
Or,
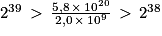
Donc n = 38.
Le nombre maximal de demi-vies est 38.
Q6.
En utilisant le nombre de demi-vies calculé à la question précédente et le temps de demi-vie du noyau de rubidium indiqué dans les données, on peut calculer le temps qu'il faudrait pour que le nombre de noyaux atteigne Nmin. La durée trouvée peut être comparée à l'âge de la Terre ou l'âge de l'univers : si elle est supérieure, alors le rubidium est adapté pour dater un échantillon de roche du site.
On peut dater un échantillon de 1 g de roche du site de Meymac jusqu'à 38 demi-vies, soit :
38 × t1/2 = 38 × 49,2 × 109 = 1,87 × 1012 a
Cette durée est très supérieure à l'âge de l'univers (de l'ordre de 108 années).
Le rubidium 87 est donc adapté pour dater un échantillon de 1 g de roche du site de Meymac.
38 × t1/2 = 38 × 49,2 × 109 = 1,87 × 1012 a
Cette durée est très supérieure à l'âge de l'univers (de l'ordre de 108 années).
Le rubidium 87 est donc adapté pour dater un échantillon de 1 g de roche du site de Meymac.
2. Décroissance radioactive du rubidium 87 dans une roche
Q7.
Il faut dériver l'expression de NRb (t) donnée dans la question : si on retrouve la même expression que dans l'équation différentielle donnée 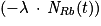 , alors l'expression est solution de l'équation. Il faut utiliser dans cette question la dérivée de la fonction exponentielle :
, alors l'expression est solution de l'équation. Il faut utiliser dans cette question la dérivée de la fonction exponentielle : 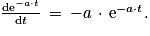
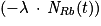 , alors l'expression est solution de l'équation. Il faut utiliser dans cette question la dérivée de la fonction exponentielle :
, alors l'expression est solution de l'équation. Il faut utiliser dans cette question la dérivée de la fonction exponentielle : 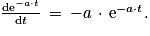
On dérive :
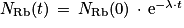
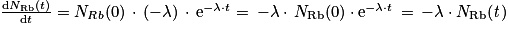
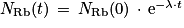 est donc bien solution de l'équation différentielle.
est donc bien solution de l'équation différentielle.
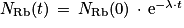
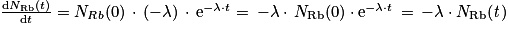
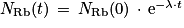 est donc bien solution de l'équation différentielle.
est donc bien solution de l'équation différentielle.Q8.
Au temps tf, le nombre de noyaux de rubidium restants est égal à Nmin. Il faut isoler tf de l'expression 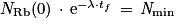 .
.
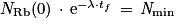 .
.Au temps tf, NRb(tf) = Nmin
donc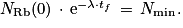
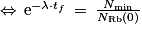
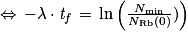
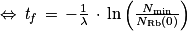
donc
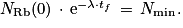
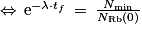
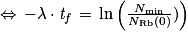
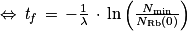
Q9.
Il s'agit d'une application numérique : le temps obtenu sera en années si aucune conversion n'est effectuée.
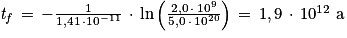
On retrouve une durée inférieure à 38 demi-vies, ce qui est cohérent avec la question 6.
3. Datation d'une roche du site de Meymac au strontium 87
Q10.
Il faut s'aider de l'équation 1 présente dans l'énoncé, sachant qu'un noyau de rubidium 87 qui disparaît donne un noyau de strontium 87.
Sachant qu'un noyau de rubidium 87 se désintègre pour former un noyau de strontium 87 :
NSr formé (t) = NRb désintégré (t)
Or NRb (t) = NRb (0) − NRb désintégré (t)
Donc : NSr formé (t) = NRb (0) − NRb (t)
NSr formé (t) = NRb désintégré (t)
Or NRb (t) = NRb (0) − NRb désintégré (t)
Donc : NSr formé (t) = NRb (0) − NRb (t)
Q11.
On peut retrouver l'équation 2 présentée dans l'énoncé en utilisant la relation déterminée à la question précédente et en factorisant les termes. Il faut se souvenir que 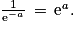
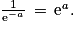
NSr formé (t) = NRb (0) − NRb (t)
Or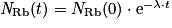 , c'est-à-dire
, c'est-à-dire 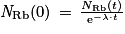
Donc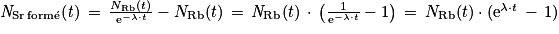 .
.
Or
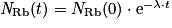 , c'est-à-dire
, c'est-à-dire 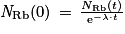
Donc
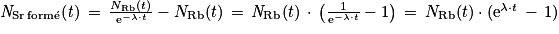 .
.Q12.
Il s'agit d'utiliser la régression linéaire fournie, de déterminer l'expression du coefficient directeur par identification avec l'équation 3 et d'en déduire le temps.
D'après l'énoncé, l'équation 3 s'écrit 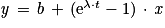 , ce qui correspond à l'équation d'une droite y = f(x) de coefficient directeur égal à
, ce qui correspond à l'équation d'une droite y = f(x) de coefficient directeur égal à 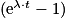 .
.
D'après l'équation de la droite sur la figure 1, le coefficient directeur est égal à 0,0042.
Donc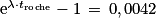
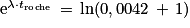
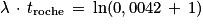
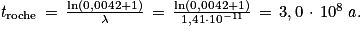
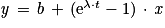 , ce qui correspond à l'équation d'une droite y = f(x) de coefficient directeur égal à
, ce qui correspond à l'équation d'une droite y = f(x) de coefficient directeur égal à 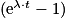 .
.D'après l'équation de la droite sur la figure 1, le coefficient directeur est égal à 0,0042.
Donc