Énoncé
Exercice sur 5 points
Les deux parties peuvent être traitées indépendamment.
Dans cet exercice, on s'intéresse à des personnes venues séjourner dans un centre multisports au cours d'un week-end.
Les résultats des probabilités demandées seront arrondis au millième si nécessaire.
Dans cet exercice, on s'intéresse à des personnes venues séjourner dans un centre multisports au cours d'un week-end.
Les résultats des probabilités demandées seront arrondis au millième si nécessaire.
Partie A
Le centre propose aux personnes venues pour un week-end une formule d'initiation au roller composée de deux séances de cours. On choisit au hasard une personne parmi celles ayant souscrit à cette formule.
On désigne par A et B les évènements suivants :
On désigne par A et B les évènements suivants :
• A : « La personne chute pendant la première séance » ;
• B : « La personne chute pendant la deuxième séance ».
Pour un évènement E quelconque, on note P(E) sa probabilité et 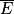 son évènement contraire.
son évènement contraire.
Des observations permettent d'admettre que P(A) = 0,6.
De plus, on constate que :
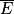 son évènement contraire.
son évènement contraire.Des observations permettent d'admettre que P(A) = 0,6.
De plus, on constate que :
• si la personne chute pendant la première séance, la probabilité qu'elle chute pendant la deuxième est 0,3 ;
• si la personne ne chute pas pendant la première séance, la probabilité qu'elle chute pendant la deuxième est 0,4.
1. Représenter la situation par un arbre pondéré.
2. Calculer la probabilité 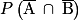 et interpréter le résultat.
et interpréter le résultat.
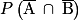 et interpréter le résultat.
et interpréter le résultat. 3. Montrer que P(B) = 0,34.
4. La personne ne chute pas pendant la deuxième séance de cours. Calculer la probabilité qu'elle n'ait pas chuté lors de la première séance.
5. On appelle X la variable aléatoire qui, à chaque échantillon de 100 personnes ayant souscrit à la formule, associe le nombre d'entre elles n'ayant chuté ni lors de la première ni lors de la deuxième séance. On assimile le choix d'un échantillon de 100 personnes à un tirage avec remise.
On admet que la probabilité qu'une personne ne chute ni lors de la première ni lors de la deuxième séance est 0,24.
On admet que la probabilité qu'une personne ne chute ni lors de la première ni lors de la deuxième séance est 0,24.
a. Montrer que la variable aléatoire X suit une loi binomiale dont on précisera les paramètres.
b. Quelle est la probabilité d'avoir, dans un échantillon de 100 personnes ayant souscrit à la formule, au moins 20 personnes qui ne chutent ni lors de la première ni lors de la deuxième séance ?
c. Calculer l'espérance E(X) et interpréter le résultat dans le contexte de l'exercice.
Partie B
On choisit au hasard une personne venue un week-end au centre multisports. On note T1 la variable aléatoire donnant son temps d'attente total en minutes avant les accès aux activités sportives pendant la journée du samedi, et T2 la variable aléatoire donnant son temps d'attente total en minutes avant les accès aux activités sportives pendant la journée du dimanche.
On admet que :
On admet que :
• T1 suit une loi de probabilité d'espérance E(T1) = 40 et d'écart-type σ(T1) = 10 ;
• T2 suit une loi de probabilité d'espérance E(T2) = 60 et d'écart-type σ(T2) = 16 ;
• les variables aléatoires T1 et T2 sont indépendantes.
On note T la variable aléatoire donnant le temps total d'attente avant les accès aux activités sportives lors des deux jours, exprimé en minutes. Ainsi, on a T = T1 + T2.
1. Déterminer l'espérance E(T) de la variable aléatoire T. Interpréter le résultat dans le contexte de l'exercice.
2. Montrer que la variance V(T) de la variable aléatoire T est égale à 356.
3. À l'aide de l'inégalité de Bienaymé-Tchebychev, montrer que, pour une personne choisie au hasard parmi celles venues un week-end au centre multisports, la probabilité que son temps total d'attente T soit strictement compris entre 60 et 140 minutes est supérieure à 0,77.
Corrigé
Partie A
1.
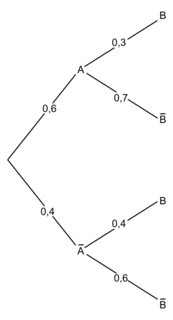 |
En effet :
• 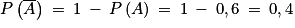 ;
;
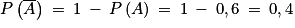 ;
;• 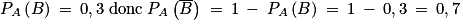 ;
;
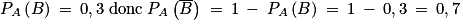 ;
;• 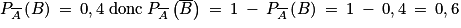
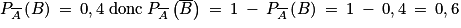
2. 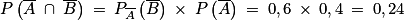 ;
;
La probabilité que la personne ne chute pas pendant la première séance et ne chute pas pendant la seconde séance est égale à 0,24.
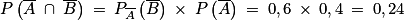 ;
;La probabilité que la personne ne chute pas pendant la première séance et ne chute pas pendant la seconde séance est égale à 0,24.
À retenir :
L'union de deux évènements se note avec le symbole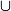 (comme dans le mot union) et il se traduit en français par le connecteur « ou ».
(comme dans le mot union) et il se traduit en français par le connecteur « ou ».
L'intersection de deux évènements se note avec le symbole et il se traduit en français par le connecteur « et » (il y a la lettre « t » dans le mot intersection).
et il se traduit en français par le connecteur « et » (il y a la lettre « t » dans le mot intersection).
L'union de deux évènements se note avec le symbole
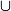 (comme dans le mot union) et il se traduit en français par le connecteur « ou ».
(comme dans le mot union) et il se traduit en français par le connecteur « ou ».L'intersection de deux évènements se note avec le symbole
 et il se traduit en français par le connecteur « et » (il y a la lettre « t » dans le mot intersection).
et il se traduit en français par le connecteur « et » (il y a la lettre « t » dans le mot intersection).3. 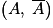 est une partition de l'univers Ω. En effet,
est une partition de l'univers Ω. En effet, 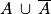 = Ω et
= Ω et 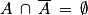 .
.
Ainsi, d'après la loi des probabilités totales, on a :
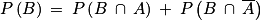
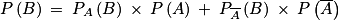
P(B) = 0,3 × 0,6 + 0,4 × 0,4
P(B) = 0,18 + 0,16
P(B) = 0,34
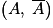 est une partition de l'univers Ω. En effet,
est une partition de l'univers Ω. En effet, 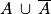 = Ω et
= Ω et 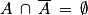 .
.Ainsi, d'après la loi des probabilités totales, on a :
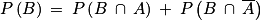
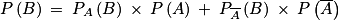
P(B) = 0,3 × 0,6 + 0,4 × 0,4
P(B) = 0,18 + 0,16
P(B) = 0,34
4. On cherche à calculer la probabilité que l'évènement 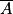 se réalise, sachant que l'évènement
se réalise, sachant que l'évènement 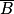 est réalisé.
est réalisé.
On doit donc calculer la probabilité conditionnelle suivante :
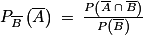
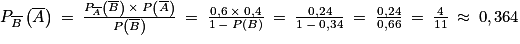
Donc la probabilité que la personne n'ait pas chuté lors de la première séance, sachant qu'elle ne chute pas pendant la deuxième séance, est 0,364.
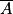 se réalise, sachant que l'évènement
se réalise, sachant que l'évènement 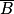 est réalisé.
est réalisé.On doit donc calculer la probabilité conditionnelle suivante :
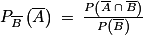
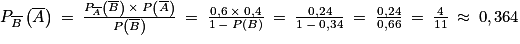
Donc la probabilité que la personne n'ait pas chuté lors de la première séance, sachant qu'elle ne chute pas pendant la deuxième séance, est 0,364.
5. a. On assimile le choix d'un échantillon de 100 personnes à un tirage avec remise, donc on répète de manière identique et indépendante n = 100 fois l'épreuve de Bernoulli « choisir une personne » dont le succès « la personne ne chute ni lors de la première ni lors de la deuxième séance » a pour probabilité p = 0,24.
Soit X la variable aléatoire discrète qui compte le nombre de succès.
Alors X suit la loi binomiale de paramètres n = 100 et p = 0,24.
Soit X la variable aléatoire discrète qui compte le nombre de succès.
Alors X suit la loi binomiale de paramètres n = 100 et p = 0,24.
b. On doit calculer la probabilité de l'évènement {X ≥ 20}.
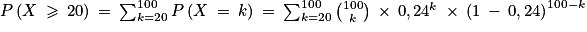
donc P(X ≥ 20) ≈ 0,855.
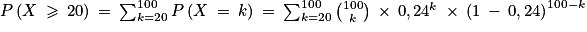
donc P(X ≥ 20) ≈ 0,855.
 Certaines calculatrices donnent directement la réponse sans avoir à utiliser le symbole « Sigma ».
Certaines calculatrices donnent directement la réponse sans avoir à utiliser le symbole « Sigma ». On peut aussi raisonner en utilisant l'astuce de l'évènement contraire, car certaines calculatrices ne proposent que les raccourcis P(X = k) et P(X ≤ k) :
On peut aussi raisonner en utilisant l'astuce de l'évènement contraire, car certaines calculatrices ne proposent que les raccourcis P(X = k) et P(X ≤ k) :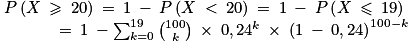
c. Comme X suit la loi binomiale de paramètres n = 100 et p = 0,24, alors :
E(X) = n × p = 100 × 0,24 = 24
E(X) = n × p = 100 × 0,24 = 24
Cela signifie que si l'on choisit un très grand nombre d'échantillons de taille n = 100, en moyenne on observerait que, sur 100 personnes, 24 personnes ne chutent ni lors de la première ni lors de la deuxième séance.
Partie B
1.
E(T) = E(T1 + T2 ) = E(T1 ) + E(T2 ) = 40 + 60 = 100.
Cela signifie que si l'on choisit un très grand nombre de personnes venues un week-end au centre multisports, on observerait par personne un temps d'attente total moyen lors des 2 jours de 100 minutes soit 1 h 40.
2. V(T) = V(T1 + T2 ) = V(T1 ) + V(T2 ) car T1 et T2 sont indépendantes.
De plus V(T1 ) = σ(T1)2 car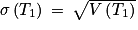
Ainsi V(T1 ) = 102 = 100.
De la même manière V(T2 ) = 162 = 256.
Ainsi V(T) = 100 + 256 = 356.
De plus V(T1 ) = σ(T1)2 car
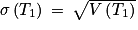
Ainsi V(T1 ) = 102 = 100.
De la même manière V(T2 ) = 162 = 256.
Ainsi V(T) = 100 + 256 = 356.
3. On a 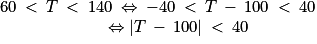
Donc, on cherche P(|T − 100| < 40) = 1 − P(|T − 100| ≥ 40)
L'inégalité de Bienaymé-Tchebychev affirme que :
Pour tout réel strictement positif δ :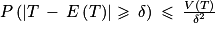
On a donc, avec δ = 40 :
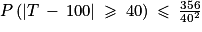
P(|T−100| ≥ 40) ≤ 0,2225
−P(|T−100| ≥ 40) ≥ −0,2225
1−P(|T−100| ≥ 40) ≥ 1−0,2225
P(|T − 100| < 40) ≥ 0,7775 ≥ 0,77
donc la probabilité que la personne ait attendu entre 60 et 140 minutes durant le week-end est supérieure à 0,77.
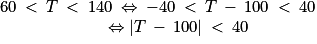
Donc, on cherche P(|T − 100| < 40) = 1 − P(|T − 100| ≥ 40)
L'inégalité de Bienaymé-Tchebychev affirme que :
Pour tout réel strictement positif δ :
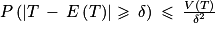
On a donc, avec δ = 40 :
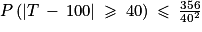
P(|T−100| ≥ 40) ≤ 0,2225
−P(|T−100| ≥ 40) ≥ −0,2225
1−P(|T−100| ≥ 40) ≥ 1−0,2225
P(|T − 100| < 40) ≥ 0,7775 ≥ 0,77
donc la probabilité que la personne ait attendu entre 60 et 140 minutes durant le week-end est supérieure à 0,77.

