Énoncé
Exercice sur 7 points
Cet exercice est un questionnaire à choix multiples.
Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.
Aucune justification n'est demandée.
Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Les six questions sont indépendantes.
Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.
Aucune justification n'est demandée.
Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Les six questions sont indépendantes.
1. La courbe représentative de la fonction f définie sur  par
par 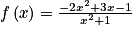 admet pour asymptote la droite d'équation :
admet pour asymptote la droite d'équation :
 par
par 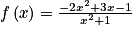 admet pour asymptote la droite d'équation :
admet pour asymptote la droite d'équation :a. x = −2
b. y = −1
c. y = −2
d. y = 0
Pour résoudre cette question, il faut connaître le lien entre asymptote d'une courbe et limite de la fonction associée. Pour trouver la limite de cette fonction, il faut utiliser la technique usuelle de factorisation par le terme de plus haut degré, sinon c'est une FI.
2. Soit f la fonction définie sur  par
par 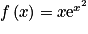 .
.
La primitive F de f sur qui vérifie F(0) = 1 est définie par :
qui vérifie F(0) = 1 est définie par :
 par
par 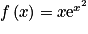 .
.La primitive F de f sur
 qui vérifie F(0) = 1 est définie par :
qui vérifie F(0) = 1 est définie par :a. 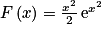
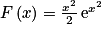
b. 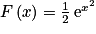
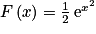
c. 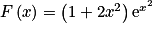
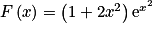
d. 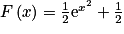
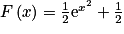
Pour résoudre cette question, vous devez connaître les primitives usuelles et utiliser la primitive de la fonction donnée, qui est la composée de la fonction carrée et de la fonction exponentielle, sans oublier d'utiliser la condition initiale.
Certaines réponses peuvent être éliminées en dérivant la fonction F proposée et en observant que l'on n'obtient pas la fonction f initiale.
Certaines réponses peuvent être éliminées en dérivant la fonction F proposée et en observant que l'on n'obtient pas la fonction f initiale.
3. On donne ci-contre la représentation graphique Cf' de la fonction dérivée f' d'une fonction f définie sur  . On peut affirmer que la fonction f est :
. On peut affirmer que la fonction f est :
 . On peut affirmer que la fonction f est :
. On peut affirmer que la fonction f est : 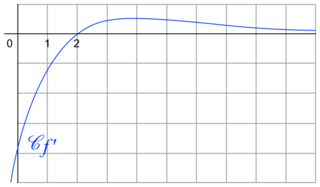 |
a. concave sur ]0 ; +∞[
b. convexe sur ]0 ; +∞[
c. convexe sur [0 ; 2]
d. convexe sur [2 ; +∞[
La convexité d'une fonction dépend du signe de sa dérivée seconde et donc aussi des variations de sa dérivée. En observant la représentation graphique de la dérivée de la fonction, on obtient les variations de cette dérivée et on peut donc répondre à la question.
4. Parmi les primitives de la fonction f définie sur  par
par 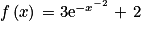 :
:
 par
par 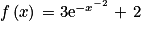 :
:a. toutes sont croissantes sur 

b. toutes sont décroissantes sur 

c. certaines sont croissantes sur  et d'autres sont décroissantes sur
et d'autres sont décroissantes sur 
 et d'autres sont décroissantes sur
et d'autres sont décroissantes sur 
d. toutes sont croissantes sur ]−∞ ; 0] et décroissantes sur [0 ; +∞[
Les variations des primitives de la fonction f dépendent du signe de cette fonction f. Il faut donc chercher ce signe pour répondre à la question.
5. La limite en +∞ de la fonction f définie sur l'intervalle ]0 ; +∞[ par 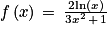 est égale à :
est égale à :
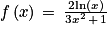 est égale à :
est égale à :a. 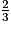
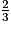
b. +∞
c. −∞
d. 0
Pour trouver la limite de cette fonction, il faut utiliser la technique usuelle de factorisation par le terme de plus haut degré, sinon c'est une FI. Il faut également connaître les formules de croissances comparées, car cette fonction est un quotient d'une fonction logarithmique et d'une fonction polynomiale.
6. L'équation e2x + ex −12 = 0 admet dans  :
:
 :
:a. trois solutions
b. deux solutions
c. une seule solution
d. aucune solution
Pour résoudre une équation avec la fonction exponentielle, il faut utiliser un changement de variable afin de revenir à la résolution d'une équation polynomiale classique. Par contre, il faut bien penser à vérifier les solutions obtenues pour savoir si elles sont possibles avec le changement de variable effectué.
Corrigé
1. Réponse c : y = −2
Soit f définie sur par
par 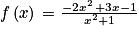 .
.
Pour x ≠ 0, on a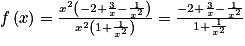 donc
donc 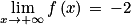 .
.
La droite horizontale d'équation y = −2 est bien une asymptote à la courbe représentative de la fonction f.
Soit f définie sur
 par
par 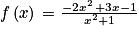 .
.Pour x ≠ 0, on a
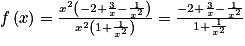 donc
donc 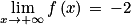 .
.La droite horizontale d'équation y = −2 est bien une asymptote à la courbe représentative de la fonction f.
2. Réponse d : 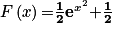
La fonction f est continue sur et admet donc des primitives. Soit F une primitive de f.
et admet donc des primitives. Soit F une primitive de f.
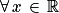 , f(x) est de la forme u'(x) × eu(x) et admet pour primitives les fonctions de la forme :
, f(x) est de la forme u'(x) × eu(x) et admet pour primitives les fonctions de la forme : 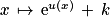 ,
,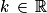 .
.
En posant u(x) = x2 et u'(x) = 2x et en remarquant que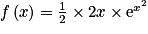 , on peut donc écrire :
, on peut donc écrire : 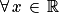 ,
, 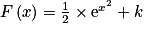 .
.
Sachant que F(0) = 1, on en déduit que :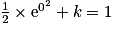 soit
soit 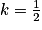 .
.
Donc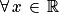 ,
, 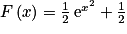 .
.
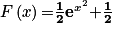
La fonction f est continue sur
 et admet donc des primitives. Soit F une primitive de f.
et admet donc des primitives. Soit F une primitive de f.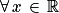 , f(x) est de la forme u'(x) × eu(x) et admet pour primitives les fonctions de la forme :
, f(x) est de la forme u'(x) × eu(x) et admet pour primitives les fonctions de la forme : 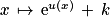 ,
,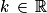 .
.En posant u(x) = x2 et u'(x) = 2x et en remarquant que
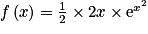 , on peut donc écrire :
, on peut donc écrire : 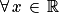 ,
, 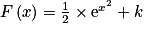 .
.Sachant que F(0) = 1, on en déduit que :
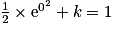 soit
soit 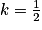 .
.Donc
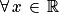 ,
, 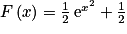 .
.3. Réponse c : convexe sur [0 ; 2]
La courbe représentative est celle de la fonction f'. Avec la précision permise par le graphique, on peut affirmer que la fonction f' est croissante sur ]−∞ ; 3] et décroissante sur [3 ; +∞[. Comme on a :![\left [0\: ;\: 2 \right ]\subset \: \left ]-\infty \: ;\: 3 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde23_m24.png) , alors f' est croissante [0 ; 2]. La fonction est donc convexe sur [0 ; 2].
, alors f' est croissante [0 ; 2]. La fonction est donc convexe sur [0 ; 2].
La courbe représentative est celle de la fonction f'. Avec la précision permise par le graphique, on peut affirmer que la fonction f' est croissante sur ]−∞ ; 3] et décroissante sur [3 ; +∞[. Comme on a :
![\left [0\: ;\: 2 \right ]\subset \: \left ]-\infty \: ;\: 3 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde23_m24.png) , alors f' est croissante [0 ; 2]. La fonction est donc convexe sur [0 ; 2].
, alors f' est croissante [0 ; 2]. La fonction est donc convexe sur [0 ; 2].4. Réponse a : toutes sont croissantes sur 
La fonction f définie sur par
par 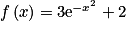 est continue et dérivable.
est continue et dérivable.
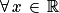 , f(x) > 0, car la fonction exponentielle est positive sur
, f(x) > 0, car la fonction exponentielle est positive sur  .
.
Les primitives F de la fonction f ont pour dérivée f, qui est positive sur .
.
Donc les fonctions F sont croissantes sur .
.

La fonction f définie sur
 par
par 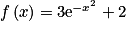 est continue et dérivable.
est continue et dérivable.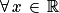 , f(x) > 0, car la fonction exponentielle est positive sur
, f(x) > 0, car la fonction exponentielle est positive sur  .
.Les primitives F de la fonction f ont pour dérivée f, qui est positive sur
 .
.Donc les fonctions F sont croissantes sur
 .
.5. Réponse d : 0
![\forall\, x\, \in \left ]0\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde23_m27.png) ,
, 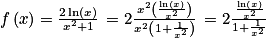 .
.
Nous savons que :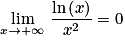 (d'après les propriétés de croissances comparées) et
(d'après les propriétés de croissances comparées) et 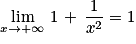 donc
donc 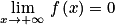 .
.
![\forall\, x\, \in \left ]0\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde23_m27.png) ,
, 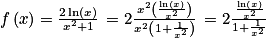 .
.Nous savons que :
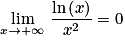 (d'après les propriétés de croissances comparées) et
(d'après les propriétés de croissances comparées) et 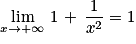 donc
donc 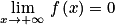 .
.6. Réponse c : une seule solution
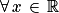 , l'équation (E) :
, l'équation (E) : 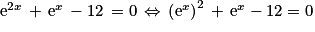 .
.
On pose alors comme changement de variable : X = ex et on obtient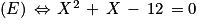 . Cette équation du second degré à une inconnue a pour solutions X = −4 et X = 3 (on peut utiliser le discriminant ici).
. Cette équation du second degré à une inconnue a pour solutions X = −4 et X = 3 (on peut utiliser le discriminant ici).
Or X = ex > 0 donc l'unique solution possible sera celle de l'équation X = 3 soit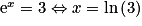 .
.
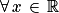 , l'équation (E) :
, l'équation (E) : 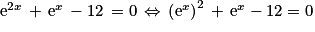 .
.On pose alors comme changement de variable : X = ex et on obtient
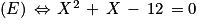 . Cette équation du second degré à une inconnue a pour solutions X = −4 et X = 3 (on peut utiliser le discriminant ici).
. Cette équation du second degré à une inconnue a pour solutions X = −4 et X = 3 (on peut utiliser le discriminant ici).Or X = ex > 0 donc l'unique solution possible sera celle de l'équation X = 3 soit
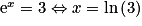 .
.
