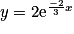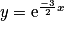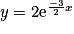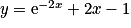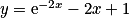En pratique, déterminer une primitive d'une fonction, c'est chercher une fonction dont la dérivée est la fonction donnée. Pour une fonction puissance, ou plus généralement une fonction polynôme, cette détermination est facile : il suffit d'augmenter d'une unité l'exposant. C'est plus difficile dans le cas d'une fonction rationnelle ; en particulier, la recherche d'une primitive de la fonction inverse conduit à une définition de la fonction logarithme népérien. Le calcul intégral et la résolution d'équations différentielles sont les applications directes de la détermination de primitives.
I. Comment reconnaître une primitive d'une fonction ?
Trouver une primitive d'une fonction f, c'est trouver une fonction dont la dérivée est la fonction f donnée.
Propriété : Soit f une fonction définie et dérivable sur un intervalle [a ; b]. F est une primitive de f si et seulement si pour tout![x\in \left [ a\, ;b \right ],\: {F}'\left ( x \right )=f\left ( x \right )](https://static1.assistancescolaire.com/t/images/t_spemat_11_m1.png) .
.
Propriété : Il existe une infinité de primitives d'une fonction donnée. Elles sont définies à une constante près. Si F est une primitive de f, alors pour tout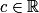 , F + c est aussi une primitive de f.
, F + c est aussi une primitive de f.
Propriété : Soit f une fonction définie et dérivable sur un intervalle [a ; b]. F est une primitive de f si et seulement si pour tout
![x\in \left [ a\, ;b \right ],\: {F}'\left ( x \right )=f\left ( x \right )](https://static1.assistancescolaire.com/t/images/t_spemat_11_m1.png) .
.Propriété : Il existe une infinité de primitives d'une fonction donnée. Elles sont définies à une constante près. Si F est une primitive de f, alors pour tout
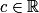 , F + c est aussi une primitive de f.
, F + c est aussi une primitive de f.Opérations et primitives usuelles
Propriété :
• Si F et G sont des primitives respectivement des fonctions f et g sur un intervalle I, alors F + G est une primitive de f + g sur I.
• Si F est une primitive de la fonction f sur un intervalle I, et c un réel, alors c × F est une primitive de c × f sur I.
On a le tableau des primitives usuelles suivant :
On a le tableau des primitives usuelles suivant :
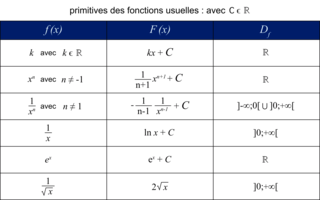 |
II. Quelles sont les primitives des fonctions polynômes ?
Propriété : Les fonctions puissance définies sur 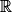 par f(x) = xn,
par f(x) = xn, 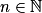 , ont pour primitives les fonctions
, ont pour primitives les fonctions 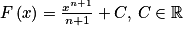 .
.
Une fonction polynôme est la somme de fonctions puissance. Pour en trouver une primitive, il suffit de chercher une primitive de chacun des termes.
Exemple : Soit f(x) = x2 + 2x + 1 définie sur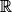 .
.
Une primitive de f est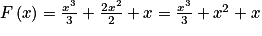 .
.
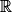 par f(x) = xn,
par f(x) = xn, 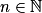 , ont pour primitives les fonctions
, ont pour primitives les fonctions 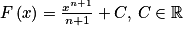 .
.Une fonction polynôme est la somme de fonctions puissance. Pour en trouver une primitive, il suffit de chercher une primitive de chacun des termes.
Exemple : Soit f(x) = x2 + 2x + 1 définie sur
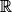 .
.Une primitive de f est
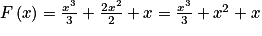 .
.III. Quelles sont les primitives des fonctions inverse ?
On peut généraliser aux exposants entiers relatifs n, 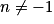 , la forme générale des primitives des fonctions puissances.
, la forme générale des primitives des fonctions puissances.
Propriété : Les fonctions inverses, définies sur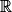 * par f(x) = xn, n entier négatif,
* par f(x) = xn, n entier négatif, 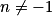 , ont pour primitives les fonctions
, ont pour primitives les fonctions 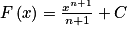 , sur ]
, sur ]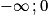 [ ou ]
[ ou ]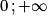 [.
[.
Propriété : Sur ]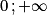 [, la fonction logarithme népérien est la primitive F de la fonction inverse
[, la fonction logarithme népérien est la primitive F de la fonction inverse 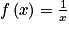 telle que F(1) = 0.
telle que F(1) = 0.
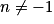 , la forme générale des primitives des fonctions puissances.
, la forme générale des primitives des fonctions puissances.Propriété : Les fonctions inverses, définies sur
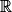 * par f(x) = xn, n entier négatif,
* par f(x) = xn, n entier négatif, 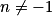 , ont pour primitives les fonctions
, ont pour primitives les fonctions 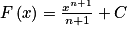 , sur ]
, sur ]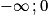 [ ou ]
[ ou ]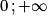 [.
[.Propriété : Sur ]
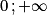 [, la fonction logarithme népérien est la primitive F de la fonction inverse
[, la fonction logarithme népérien est la primitive F de la fonction inverse 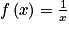 telle que F(1) = 0.
telle que F(1) = 0.IV. Comment calculer une primitive d'une fonction composée ?
Les fonctions définies sur 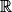 par
par 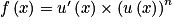 ,
, 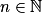 , ont pour primitives les fonctions
, ont pour primitives les fonctions 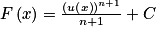 ,
, 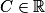 .
.
Les fonctions définies pour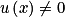 par
par 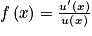 ont pour primitives les fonctions
ont pour primitives les fonctions 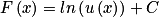 ,
, 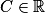 .
.
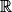 par
par 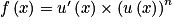 ,
, 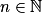 , ont pour primitives les fonctions
, ont pour primitives les fonctions 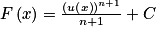 ,
, 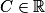 .
.Les fonctions définies pour
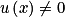 par
par 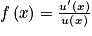 ont pour primitives les fonctions
ont pour primitives les fonctions 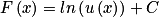 ,
, 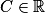 .
.V. Comment déterminer une primitive d'une fonction rationnelle ?
Pour déterminer une primitive d'une fonction rationnelle, on décompose celle-ci en une somme d'une fonction polynôme et d'une fonction inverse.Exemple : Soit
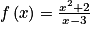 définie sur ]
définie sur ]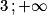 [. Elle peut s'écrire sous la forme :
[. Elle peut s'écrire sous la forme : 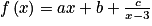 .
.On réduit au même dénominateur :
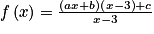 .
.On développe le numérateur :
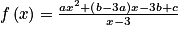 .
.Par identification des coefficients des termes de même degré du numérateur, on obtient le système :
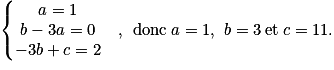
On a donc
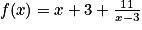 .
.On en déduit une primitive
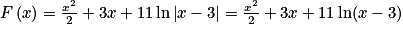 , car x − 3 > 0 sur ]
, car x − 3 > 0 sur ]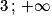 [.
[.VI. Qu'est-ce qu'une équation différentielle ?
Les équations différentielles sont des égalités dans lesquelles apparaissent une fonction et au moins l'une de ses dérivées successives. L'ordre de l'équation est égal au rang le plus élevé de la dérivée.Les équations différentielles trouvent des applications en économie, en physique et en biologie.
VII. Comment résoudre une équation différentielle de premier ordre sans second membre ?
Une équation différentielle de premier ordre sans second membre est de la forme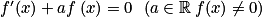 .
.De manière simplifiée, ces équations s'écrivent :
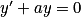 .
.Résoudre cette équation, c'est déterminer toutes les fonctions f qui conviennent.
On a :
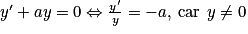 .
.Une primitive de
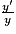 est
est 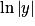 , alors on a :
, alors on a : 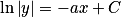 soit
soit 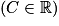 , soit
, soit 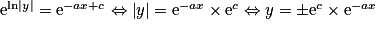 .
.En posant λ = ec (ou −ec), on en déduit la famille des fonctions solutions : y = λe−ax.
La constante λ est déterminée par l'image d'une valeur particulière de la variable.
Exemple : Soit l'équation différentielle
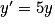 , et soit
, et soit 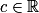 .
.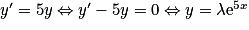 .
.Ainsi les fonctions numériques y à une variable x qui vérifient
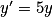 sont les fonctions définies pour tout réel x par y(x)=λe5x,
sont les fonctions définies pour tout réel x par y(x)=λe5x, 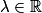 .
.Si, de plus, y(2) = 1, alors
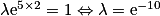 . Dans ce cas, l'unique solution est la fonction y définie sur
. Dans ce cas, l'unique solution est la fonction y définie sur 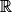 par y(x) = e5x−10.
par y(x) = e5x−10.VIII. Comment résoudre une équation différentielle de premier ordre avec second membre ?
Une équation différentielle du premier ordre avec second membre se présente sous la forme :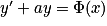 , où Φ est une fonction de variable x.
, où Φ est une fonction de variable x.Pour résoudre cette équation, on cherche une solution particulière y1 dont la forme sera donnée par l'énoncé.
Les solutions de l'équation sont alors de la forme : y = λe−ax + y1.
Exemple 1 : Soit l'équation différentielle :
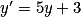 .
.Une solution particulière y1 est, par exemple,
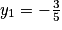 .
.Les solutions de
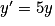 sont les fonctions y telles que y(x) = λe5x,
sont les fonctions y telles que y(x) = λe5x, 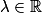 .
.Ainsi, les solutions de l'équation différentielle
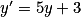 sont les fonctions y définies pour tout réel x par
sont les fonctions y définies pour tout réel x par 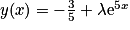 ,
, 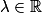 .
.Exemple 2 : Soit l'équation différentielle :
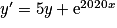 .
.On va chercher une solution particulière y1 sous la forme y1 = α(x)e5x, avec α une fonction que l'on va déterminer.
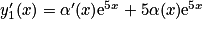 .
.Donc
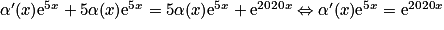 .
.Donc
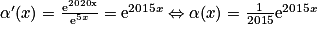 .
.Ainsi
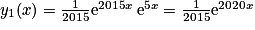 .
.Les solutions de
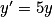 sont les fonctions y telles que y(x) = λe5x,
sont les fonctions y telles que y(x) = λe5x, 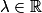 .
.Ainsi, les solutions de l'équation différentielle
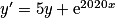 sont les fonctions y définies pour tout réel x par
sont les fonctions y définies pour tout réel x par 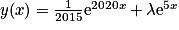 ,
, 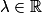 .
.Zoom sur… les primitives
Fonction dérivée
Une fonction f est dérivable sur un intervalle I si et seulement si elle est dérivable en tout point de I. Alors la fonction qui, à tout réel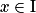 , associe le nombre dérivé de f en x est appelée fonction dérivée de f et se note
, associe le nombre dérivé de f en x est appelée fonction dérivée de f et se note 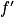 .
.Primitive
Soit f une fonction définie continue sur un intervalle I. Une primitive de la fonction f sur I est une fonction F dérivable sur I telle que, pour tout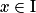 ,
, 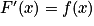 .
.Lien entre continuité et primitive
Toute fonction f continue sur un intervalle I admet une primitive F sur l'intervalle I.Plusieurs primitives pour une même fonction f
• Si F est une primitive de la fonction f sur un intervalle I, alors toutes les primitives de la fonction f sur I sont les fonctions 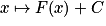 , où C est une constante réelle quelconque.
, où C est une constante réelle quelconque.
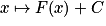 , où C est une constante réelle quelconque.
, où C est une constante réelle quelconque.• Soit I un intervalle contenant une valeur x0 et y0 un réel connu. Il existe une unique primitive F de la fonction f sur I vérifiant la condition : F(x0) = y0.
Primitives et opérations
• Soient F et G des primitives respectives des fonctions f et g sur l'intervalle I. Alors F + G est une primitive de la fonction f + g sur l'intervalle I.
• Soient F une primitive de f sur un intervalle I, et k un nombre réel. Alors k × F est une primitive de la fonction k × f sur l'intervalle I.
Tableaux des primitives usuelles
| f(x) | Une primitive F(x) |
|---|---|
| a(constante) | ax |
| x | 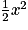 |
| xn, n> 0 | 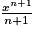 |
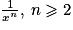 | 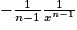 |
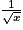 | 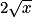 |
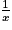 | lnx, x> 0 |
| ex | ex |
| Fonction f | Une primitive F |
|---|---|
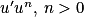 | 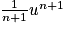 |
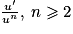 | 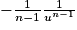 |
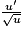 | 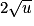 |
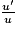 | lnu, u> 0 |
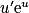 | eu |
Histoire des mathématiques : calcul différentiel
Le calcul différentiel s'est développé de concert avec la physique au XVIIe siècle. Parmi les initiateurs, Fermat, Huygens, Pascal et Barrow reconnaissent que le problème des aires (le calcul intégral) est le problème inverse de celui des tangentes (la dérivation). De plus, ils remarquent que le calcul différentiel peut être abordé à partir des travaux sur la quadrature de l'hyperbole, et qu'ils tournent tous autour de la question de « l'infiniment petit » qu'ils ne savent pas encore justifier.Les travaux de Newton et Leibniz révèlent, par la suite, deux visions différentes du calcul infinitésimal. En effet, Newton aborde souvent les mathématiques du point de vue physique (il compare la notion actuelle de limite avec la notion de vitesse instantanée, ce qui lui permet de négliger les quantités infinitésimales), alors que Leibniz l'aborde de façon philosophique (il travaille en parallèle sur l'existence de l'infiniment petit dans l'univers). La justification de telles méthodes nécessite donc une mise au point de la notion de limite qui reste intuitive à cette époque.
Des fondations solides sont finalement proposées dans le Cours d'Analyse de Cauchy (1821, 1823) qui définit précisément la notion de limites et en fait le point de départ de l'analyse.
Parallèlement, les résolutions d'équations différentielles, provenant de la mécanique ou des mathématiques, se structurent, notamment grâce au lien entre le calcul différentiel et les séries (Newton, Euler, d'Alembert, Lagrange, Cauchy, etc.), ce qui illustre les ponts entre le discret et le continu.
Exercice n°1
Quelle est la solution de l'équation 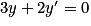 , telle que
, telle que 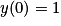 ?
?
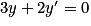 , telle que
, telle que 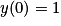 ?
? Cochez la bonne réponse.
| ||
| ||
|
L'équation équivaut à : 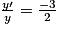 .
.
Soit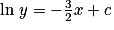 , d'où :
, d'où : 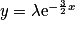 .
.
Pour x = 0 on a y = λ, d'où : λ = 1. Alors :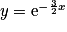 .
.
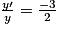 .
.Soit
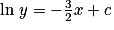 , d'où :
, d'où : 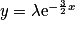 .
.Pour x = 0 on a y = λ, d'où : λ = 1. Alors :
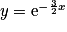 .
.Exercice n°2
Quelle est la solution de l'équation 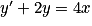 , telle que y(0) = 0 ?
, telle que y(0) = 0 ?
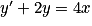 , telle que y(0) = 0 ?
, telle que y(0) = 0 ? Cochez la bonne réponse.
| ||
| ||
|
La solution générale de l'équation sans second membre 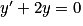 s'écrit
s'écrit 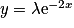 .
.
Une solution particulière est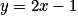 , car
, car 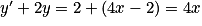 .
.
Alors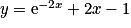 est la solution de l'équation donnée.
est la solution de l'équation donnée.
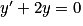 s'écrit
s'écrit 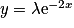 .
.Une solution particulière est
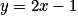 , car
, car 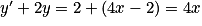 .
.Alors
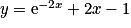 est la solution de l'équation donnée.
est la solution de l'équation donnée.