Définition
Un triangle isocèle est un triangle qui a deux côtés de même longueur.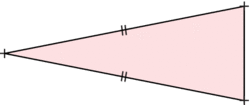 |
Remarque : on code l'égalité des longueurs en utilisant le même symbole.
Construction
Avec un écartement de compas (supérieur à la moitié de BC), pointe sèche en B, puis en C, on trace deux arcs de cercle.A est leur point d'intersection.
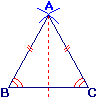 |
Propriété
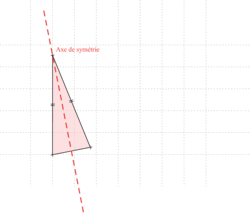
• Un triangle isocèle a un axe de symétrie.
• Un triangle avec un axe de symétrie est un triangle isocèle.
 |
Les angles d'un triangle isocèle
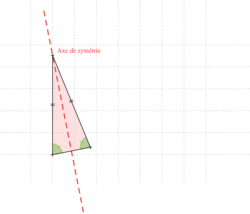
• Un triangle isocèle a deux angles de même mesure.
• Un triangle avec deux angles de même mesure est un triangle isocèle.
 |
Exercice n°1
Le triangle 1 est :
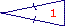 |
Cochez la bonne réponse.
| ||
| ||
|
• Un triangle isocèle a au moins deux côtés de la même longueur.
• Un triangle équilatéral a trois côtés de la même longueur.
Exercice n°2
Le triangle 2 est :
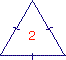 |
Cochez la bonne réponse.
| ||
| ||
|
• Un triangle isocèle a au moins deux côtés de la même longueur.
• Un triangle équilatéral a trois côtés de la même longueur.
Exercice n°3
OSU est un triangle isocèle de sommet principal S.
Trace-le sur une feuille à part, puis complète.
Écrivez les réponses dans les zones colorées.
Sachant que OSU est isocèle en S, tu peux en conclure que :
- [OS] a la même longueur que [] ;
- Les angles U et O sont égaux.
« OSU est isocèle en S », cela signifie que :
- les côtés de même longueur ont le sommet S en commun ;
- les angles égaux ont pour sommets les deux autres sommets du triangle.
Exercice n°4
Fais les exercices dans l'ordre proposé.
a. Construis sur une feuille à part :
- un segment [GD] ;
- le milieu I de [GD] ;
- la perpendiculaire en I à [GD] ;
- un point F sur la perpendiculaire.
b. Complète la phrase suivante.
Écrivez les réponses dans les zones colorées.
Le triangle GDF est en .
le point F appartient à la médiatrice du segment [GD] : il est donc à égale distance de G et de D.
Par conséquent GF = FD. Comme le triangle GDF a deux côtés de même longueur, c'est un triangle isocèle en F.
Par conséquent GF = FD. Comme le triangle GDF a deux côtés de même longueur, c'est un triangle isocèle en F.

