22 = 2 × 11.
On dit que 22 est un multiple de 2.
On dit aussi que 22 est divisible par 2 (sa division par 2 tombe juste).
On dit que 22 est un multiple de 2.
On dit aussi que 22 est divisible par 2 (sa division par 2 tombe juste).
- Un nombre entier est divisible par 2 si son chiffre des unités est 0 ; 2 ; 4 ; 6 ou 8.
- Un nombre entier est divisible par 3 si la somme de ses chiffres est un multiple de 3 (3 ; 6 ; 9 ; etc.).
- Un nombre entier est divisible par 4 si le nombre formé par ses deux derniers chiffres est un multiple de 4.
- Un nombre entier est divisible par 5 si son chiffre des unités est 0 ou 5.
- Un nombre entier est divisible par 9 si la somme de ses chiffres est un multiple de 9 (9 ; 18 ; 27 ; etc.).
- Un nombre entier est divisible par 10 si son chiffre des unités est 0.
Exercice n°1
Sélectionnez la (ou les) bonne(s) réponse(s) dans le texte.
en violet
a. Sélectionne les nombres divisibles par 5.
421 430 432 445 444
421 430 432 445 444
b. Sélectionne les nombres divisibles par 3.
713 723 753 763 783
713 723 753 763 783
c. Sélectionne les nombres divisibles par 9.
1 062 1 262 1 462 1 962
1 062 1 262 1 462 1 962
Nombres divisibles par 3 :
7 + 1 + 3 = 11
7 + 2 + 3 = 12
7 + 5 + 3 = 15
7 + 6 + 3 = 16
7 + 8 + 3 = 18
11 et 16 ne sont pas dans la table de 3.
7 + 1 + 3 = 11
7 + 2 + 3 = 12
7 + 5 + 3 = 15
7 + 6 + 3 = 16
7 + 8 + 3 = 18
11 et 16 ne sont pas dans la table de 3.
Exercice n°2
Complète les nombres suivants, et par ordre croissant, pour qu'ils soient…
a. divisibles par 5.
Écrivez les réponses dans les zones colorées.
280 28 29 29
b. divisibles par 3.
Écrivez les réponses dans les zones colorées.
642 64 64
c. divisibles par 9.
Écrivez les réponses dans les zones colorées.
75 76 77
c. La somme des chiffres du nombre doit être dans la table de 9.
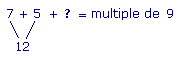 |
Le seul chiffre qui convienne est 6.
Exercice n°3
Les affirmations suivantes sont-elles vraies ou fausses ?
Coche la bonne réponse.
Coche la bonne réponse.
a. Tous les nombres terminés par 5 sont des multiples de 5.
Cochez la bonne réponse.
| ||
|
b. Tous les nombres terminés par 3 sont des multiples de 3.
Cochez la bonne réponse.
| ||
|
c. Tous les nombres terminés par un nombre pair sont divisibles par 4.
Cochez la bonne réponse.
| ||
|
d. Tous les nombres divisibles par 10 sont divisibles par 5 et 2.
Cochez la bonne réponse.
| ||
|
e. Tous les nombres divisibles par 6 ne sont divisibles que par 3.
Cochez la bonne réponse.
| ||
|
f. Tous les nombres divisibles par 7 ne sont divisibles que par 7.
Cochez la bonne réponse.
| ||
|
c. Pour qu'un nombre soit divisible par 4, il faut qu'il soit divisible par 2 et encore par 2.
e. Un nombre divisible par 6 est divisible par 3 et par 2.
f. 35 est divisible par 7 et par 5, mais 7 ne peut être divisé que par 1 ou par 7.

